- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Операции над множествами
Содержание
- 1. Презентация по теме Операции над множествами
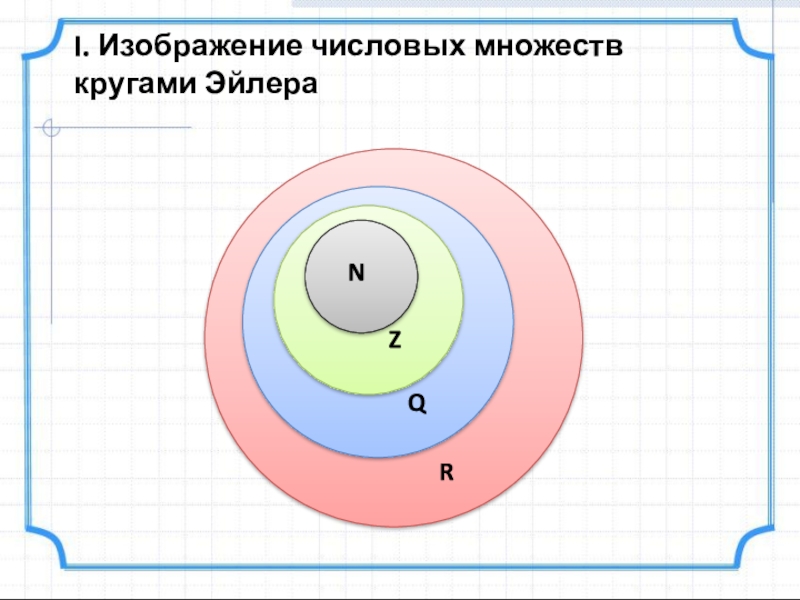
- 2. I. Изображение числовых множеств кругами Эйлера
- 3. II. Операции над множествами1) ОбъединениеA∪B={ x |
- 4. Задача №1.1. А = {2, 3, 8},
- 5. A∩B={ x | x ∈ A и
- 6. Задача №3.1. А = {2, 3, 8},
- 7. A\B={ x | x ∈ A и
- 8. A Δ B=(A\B) ∪ (B\A)A Δ B=(A∪B)
- 9. ĀВ Дополнение множества А (А ⊆ В)
- 10. Ā = U\A Дополнение множества А до
- 11. III. Порядок выполнения операций()ДополнениеПересечениеОбъединение и разность (одинаковый
- 12. IV. Решение задачЗадача №3. Найти множество, являющееся
- 13. Задача №4. Найти множество, являющееся объединением множествА
- 14. Задача №5. Найти множество, являющееся разностью множеств
- 15. Задача №6. Даны множества R = {х
- 16. Задача №7. Даны множества А = {a,
- 17. Домашнее задание*О.В.Кузьмин. Перечислительная комбинаторика§ 1.1. Конечные множества
- 18. V. Свойства операций над множествамиA∪B=B∪A(A∪B) ∪ С=
- 19. 3. ДистрибутивностьA∩(B∪С)= (A∩B)∪(A∩С) Доказательство:1) x ∈ A∩(B∪С)
- 20. 3. ДистрибутивностьA∩(B∪С)= (A∩B)∪(A∩С) Доказательство:1) …2) x ∈
- 21. 3. ДистрибутивностьA∩(B∪С)= (A∩B)∪(A∩С)Иллюстрация кругами Эйлера: A∪ (B∩С)= (A∪B)∩(A∪С)ДЗ: иллюстрация кругами ЭйлераA∩(B∪С)(A∩B)∪(A∩С)
- 22. 4. Законы де МорганаA∪В = A∩B Доказательство:1)
- 23. 4. Законы де МорганаA∪В = A∩B Доказательство:1)
- 24. 4. Законы де МорганаA∪В = A∩B Иллюстрация
- 25. А\ (В∩С) = (А\ В)∪(А\С)VI. Проведите доказательство при помощи кругов Эйлера123А\ (В∩С)(А\ В)∪(А\С)1212123
- 26. Домашнее заданиеЛицей ИГУ, liguirk.ru*О.В.Кузьмин. Перечислительная комбинаторика [1]§1.1После
Слайд 3II. Операции над множествами
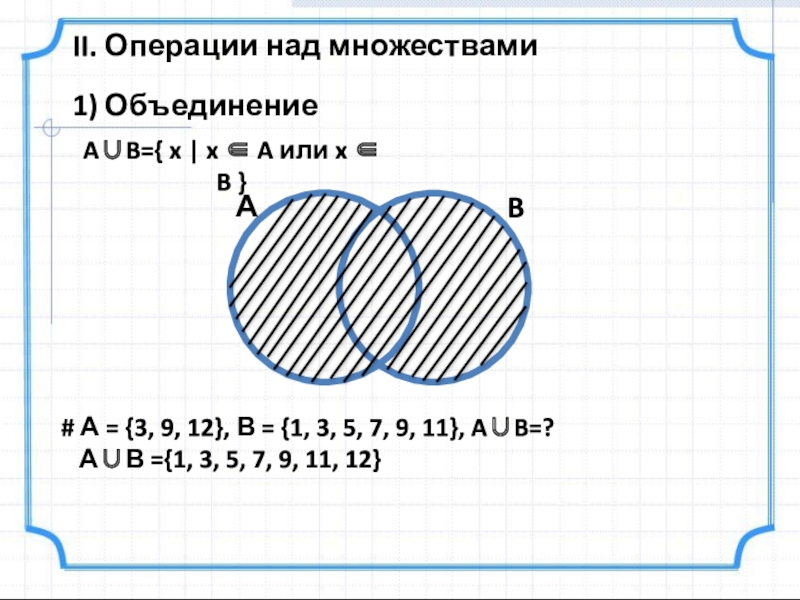
1) Объединение
A∪B={ x | x ∈ A или
# А = {3, 9, 12}, В = {1, 3, 5, 7, 9, 11}, A∪B=?
А∪В ={1, 3, 5, 7, 9, 11, 12}
Слайд 4Задача №1.
1. А = {2, 3, 8}, В = {2, 3,
Найдите:
А∪В
А∪С
С∪В
2. А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите:
А∪В
А∪С
С∪В
{2, 3, 8, 11}
{2, 3, 5, 8, 11}
{2, 3, 5, 8, 11}
{a, b, c, d, e, f}
{a, b, c, d, e, g, k}
{c, d, e, f, g, k}
Слайд 5A∩B={ x | x ∈ A и x ∈ B }
#1.
А∩В =
#2. А = {10, 20, …, 100}, В = {6, 12, 18,…}.
А∩В =
#3. А = {1, 2, 3}, В = {4, 5, 6}.
А∩В =
{3, 9}
{30, 60, 90}
∅
2) Пересечение
Слайд 6
Задача №3.
1. А = {2, 3, 8}, В = {2, 3,
Найдите:
1) А∩В
2) А∩С
3) С∩В
2. А – множества всех натуральных чисел, кратных 10,
В = {1, 2, 3, …, 41}.
А∩В =
3. А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите:
1) А∩В
2) А∩С
3) С∩В
{2, 3, 8}
{∅}
{11}
{10, 20, 30, 40}
{c, d}
{c}
{c, e}
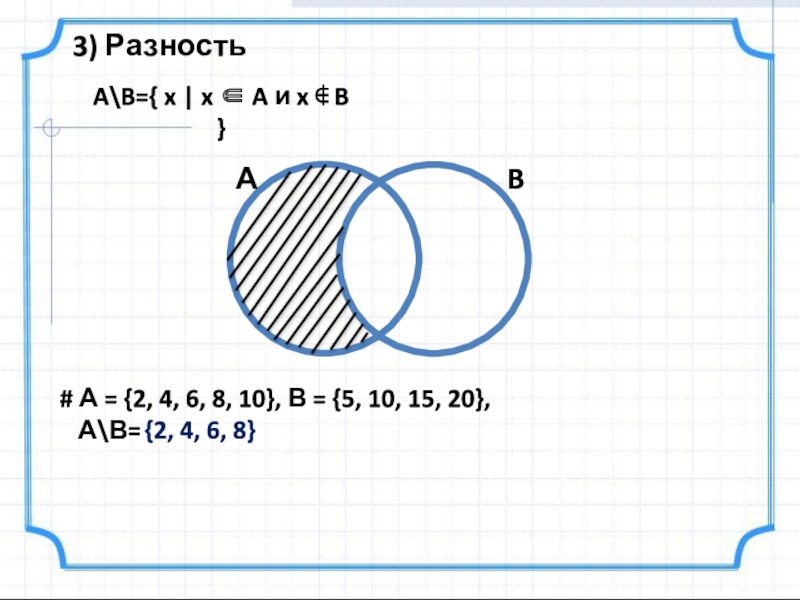
Слайд 7A\B={ x | x ∈ A и x ∉ B }
#
А\В=
{2, 4, 6, 8}
3) Разность
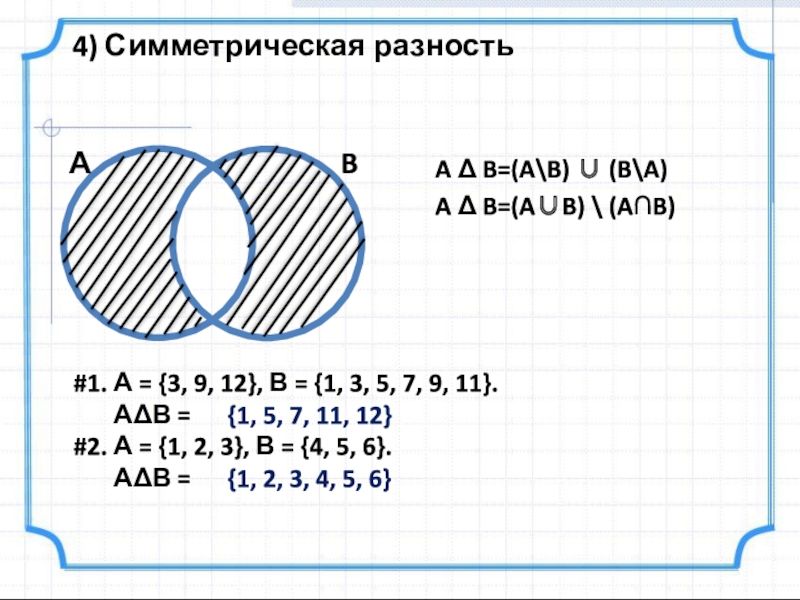
Слайд 8A Δ B=(A\B) ∪ (B\A)
A Δ B=(A∪B) \ (A∩B)
4) Симметрическая разность
#1.
АΔВ =
#2. А = {1, 2, 3}, В = {4, 5, 6}.
АΔВ =
{1, 5, 7, 11, 12}
{1, 2, 3, 4, 5, 6}
Слайд 9ĀВ
Дополнение множества А (А ⊆ В) до множества В:
ĀВ =
= { x | x ∈ В и x ∉ A }
# А = {2, 5, 9}, В = {1, 2, 5, 7, 9}
ĀВ =
4) Дополнение
{1, 7}
Слайд 10Ā = U\A
Дополнение множества А до УМ
# А - множество
В - множество собак,
С - множество коров
Назовите УМ для множеств A, B, C.
Дополнение до универсального множества (УМ):
УМ – универсум – U
Множество, содержащее все элементы, рассматриваемые в данной задаче.
U1 - множество домашних животных
U2 - множество млекопитающих
U3 - множество четвероногих
Универсальное множество - неоднозначно
Слайд 11III. Порядок выполнения операций
()
Дополнение
Пересечение
Объединение и разность (одинаковый приоритет)
#
А={3; 4; 5},
Найдите:
А∪К∩В\C
1
2
3
K∩B = {5, 7}
A∪K∩B = {3, 4, 5, 7}
A∪K∩B\C = {3, 5, 7}
Ответ: {3, 5, 7}
Слайд 12IV. Решение задач
Задача №3.
Найти множество, являющееся пересечением множеств А =
Решение
1) С = А∩В = {2, 5, 7}
2) m (C) = 3
1
10
2
7
5
3
6
9
Слайд 13Задача №4.
Найти множество, являющееся объединением множеств
А = {1, 2, 5,
Решение
С = А ∪ В = {1, 2, 3, 5, 6, 7, 9, 10}
m (C) = 8
U - множество, объединяющее множества А и В
U = {х | х ≤ 10, где х ∈ N }.
1
10
2
7
5
3
6
9
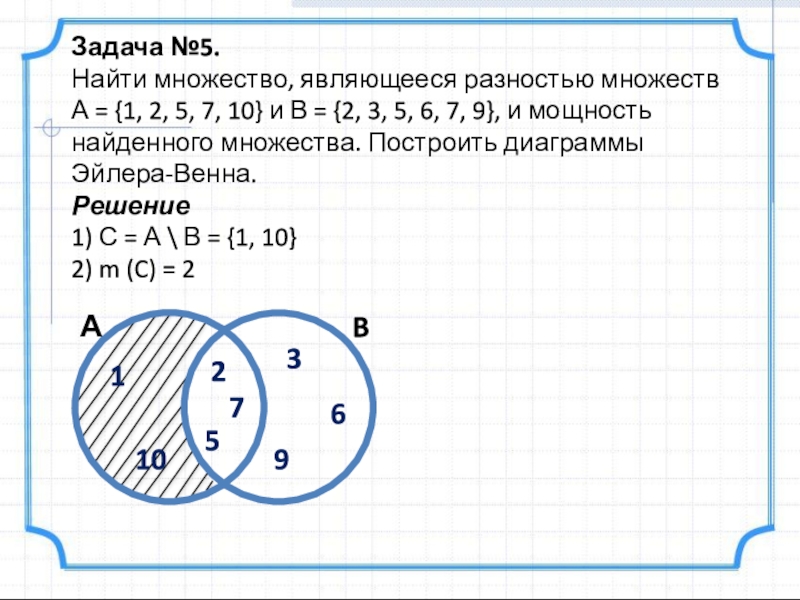
Слайд 14Задача №5.
Найти множество, являющееся разностью множеств
А = {1, 2,
Решение
1) С = А \ В = {1, 10}
2) m (C) = 2
1
10
2
7
5
3
6
9
Слайд 15Задача №6.
Даны множества R = {х | х - учитель
Решение
1) R ∩E = {z | z - учитель химии и биологии} - учителя химии и биологии одновременно.
2) R∪E = {w | w -учитель химии или биологии} - все учителя химии, биологии и учителя одновременно химии и биологии.
3) R\E = {y | y - учитель химии} - только учителя химии.
4) E\R = {t | t - учитель биологии} - только учителя биологии.
5) U = {u | u - учитель} - все учителя
Слайд 16Задача №7.
Даны множества А = {a, e, f, d, k,
Решение
С = А∪В
D - универсальное множество для А и В
Е = В\А
F = А∩В
G = A\B
Слайд 17Домашнее задание
*
О.В.Кузьмин. Перечислительная комбинаторика
§ 1.1. Конечные множества и операции над ними
(до
Задачи: 1.4, 1.5, 1.6
“2_ДЗ-1_Операции над множествами.doc”
Подготовиться к СР
Слайд 18V. Свойства операций над множествами
A∪B=B∪A
(A∪B) ∪ С= A∪(B ∪ С)
1. Коммутативность
A∩B=B∩A
2.
(A∩B) ∩ С= A∩(B ∩ С)
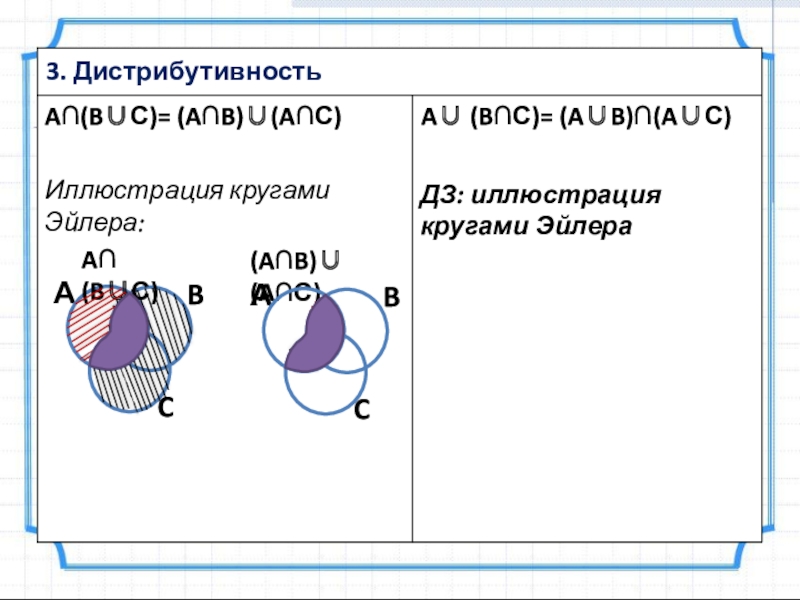
Слайд 193. Дистрибутивность
A∩(B∪С)= (A∩B)∪(A∩С)
Доказательство:
1) x ∈ A∩(B∪С) ⇒
x ∈ A и
(по опр. пересечения) ⇒
x ∈ A и одновременно или x ∈ B, или x ∈ С (по опр. объединения) ⇒
x ∈ A и одновременно x ∈ B, либо x ∈ A и одновременно x ∈ С ⇒
x ∈ (A∩B)∪(A∩С)
⇒
A∩(B∪С) ⊆ (A∩B)∪(A∩С)
A∪ (B∩С)= (A∪B)∩(A∪С)
Слайд 203. Дистрибутивность
A∩(B∪С)= (A∩B)∪(A∩С)
Доказательство:
1) …
2) x ∈ (A∩B)∪(A∩С) ⇒
x ∈ A
x ∈ A и одновременно или x ∈ B, или x ∈ С ⇒
x ∈ A и одновременно x ∈ (B∪С) ⇒
x ∈ A∩(B∪С) ⇒
(A∩B)∪(A∩С) ⊆ A∩(B∪С)
1)
2)
A∪ (B∩С)= (A∪B)∩(A∪С)
⇒
A∩(B∪С)= (A∩B)∪(A∩С)
ДЗ: провести аналогичное доказательство
Слайд 213. Дистрибутивность
A∩(B∪С)= (A∩B)∪(A∩С)
Иллюстрация кругами Эйлера:
A∪ (B∩С)= (A∪B)∩(A∪С)
ДЗ: иллюстрация кругами Эйлера
A∩(B∪С)
(A∩B)∪(A∩С)
Слайд 224. Законы де Моргана
A∪В = A∩B
Доказательство:
1) x ∈ A∪B ⇒
x ∉ A∪B
(по опр. дополнения) ⇒
x ∉ A и x ∉ B
(по опр. объединения) ⇒
x ∈ A и x ∈ B ⇒
x ∈ A∩B ⇒
A∪В ⊆ A∩B
A∩В = A∪B
Слайд 234. Законы де Моргана
A∪В = A∩B
Доказательство:
1) …
2) x ∈
x ∈ A и x ∈ B ⇒
x ∉ A и x ∉ B ⇒
x ∉ A∪B ⇒
x ∈ A∪B ⇒
A∩B ⊆ A∪В
A∩В = A∪B
Слайд 244. Законы де Моргана
A∪В = A∩B
Иллюстрация кругами Эйлера:
A∩В =
ДЗ:
1) Провести аналогичное доказательство
2) Проиллюстрировать его кругами Эйлера
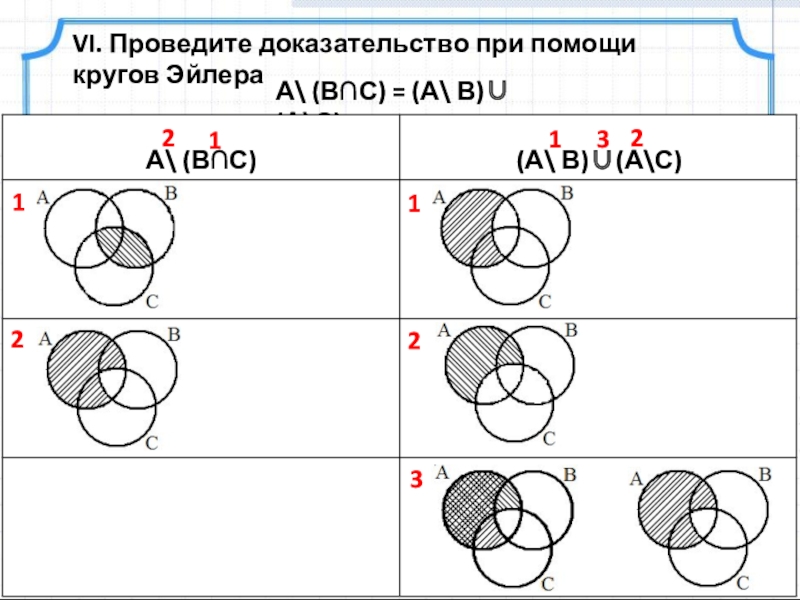
Слайд 25А\ (В∩С) = (А\ В)∪(А\С)
VI. Проведите доказательство при помощи кругов Эйлера
1
2
3
А\
(А\ В)∪(А\С)
1
2
1
2
1
2
3
Слайд 26Домашнее задание
Лицей ИГУ, liguirk.ru
*
О.В.Кузьмин. Перечислительная комбинаторика [1]
§1.1
После §1.1 : №1.7 (доказать
2-ой закон дистрибутивности, 2-ой закон де Моргана
Подготовиться к СР

















![Презентация по теме Операции над множествами Домашнее заданиеЛицей ИГУ, liguirk.ru*О.В.Кузьмин. Перечислительная комбинаторика [1]§1.1После §1.1 : №1.7 (доказать Домашнее заданиеЛицей ИГУ, liguirk.ru*О.В.Кузьмин. Перечислительная комбинаторика [1]§1.1После §1.1 : №1.7 (доказать с помощью кругов Эйлера)2-ой закон дистрибутивности,](/img/thumbs/c4a5ee537a186b695e5578778e655163-800x.jpg)





