- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Алгоритмы сортировки для дисциплины ОП.08 Теория алгоритмов
Содержание
- 1. Презентация по теме Алгоритмы сортировки для дисциплины ОП.08 Теория алгоритмов
- 2. В чем состоит задача сортировки?Зачем нужно изучать сортировку?Сортировка пузырькомСортировка выборомСортировка вставкамиСортировка слиянием
- 3. 1. В ЧЕМ СОСТОИТ ЗАДАЧА СОРТИРОВКИ?Сортировка –
- 4. 1. В ЧЕМ СОСТОИТ ЗАДАЧА СОРТИРОВКИ?Устойчивый алгоритм
- 5. 1. В ЧЕМ СОСТОИТ ЗАДАЧА СОРТИРОВКИ?Как правило,
- 6. 2. ЗАЧЕМ НУЖНО ИЗУЧАТЬ СОРТИРОВКУ?Во многих приложениях
- 7. СОРТИРОВКА ПУЗЫРЬКОМ (BUBBLE SORT)
- 8. 3. СОРТИРОВКА ПУЗЫРЬКОМСуть алгоритма: многократный проход по
- 9. 3. СОРТИРОВКА ПУЗЫРЬКОМАлгоритм Bubble sort (A[0…n-1])for i=0
- 10. СОРТИРОВКА ВЫБОРОМ (SELECTION SORT)
- 11. 4. СОРТИРОВКА ВЫБОРОМСуть алгоритма: проходим по списку,
- 12. 4. СОРТИРОВКА ВЫБОРОМАлгоритм Selection sort (A[0…n-1])for i=0
- 13. СОРТИРОВКА ВСТАВКАМИ (INSERTION SORT)
- 14. 5. СОРТИРОВКА ВСТАВКАМИСуть алгоритма: делим список на
- 15. 5. СОРТИРОВКА ВСТАВКАМИАлгоритм Insertion sort (A[0…n-1])for i=1
- 16. 5. СОРТИРОВКА ВСТАВКАМИВремя работы: O(n2) в худшем
- 17. СОРТИРОВКА СЛИЯНИЕМ (MERGE SORT)
- 18. 6. СОРТИРОВКА СЛИЯНИЕМСуть алгоритма: список рекурсивно делится
- 19. 6. СОРТИРОВКА СЛИЯНИЕМАлгоритм Mergesort (A[0…n-1])if n>1
- 20. 6. СОРТИРОВКА СЛИЯНИЕМАлгоритм Merge (B[0…p-1], C[0…q-1], A[0…p+q-1)i=0; j=0; k=0While i
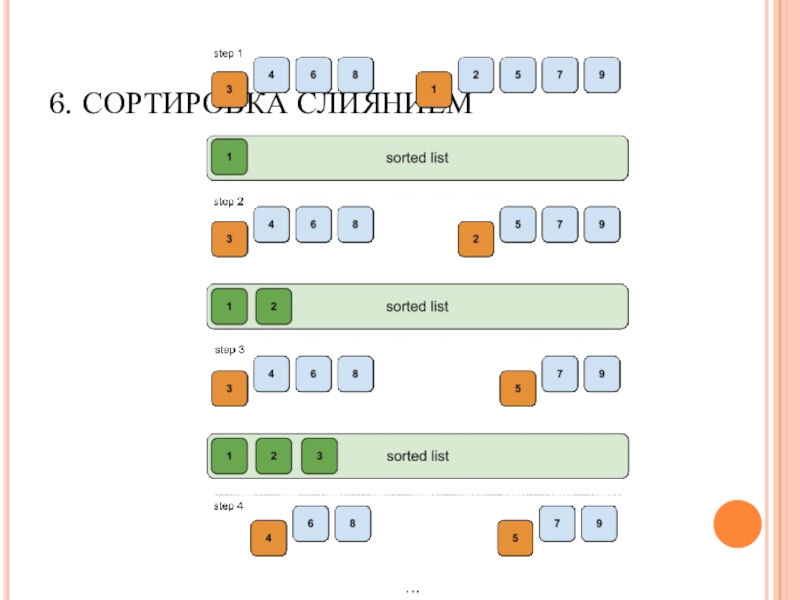
- 21. 6. СОРТИРОВКА СЛИЯНИЕМ
- 22. 6. СОРТИРОВКА СЛИЯНИЕМВремя работы: O(n log n)
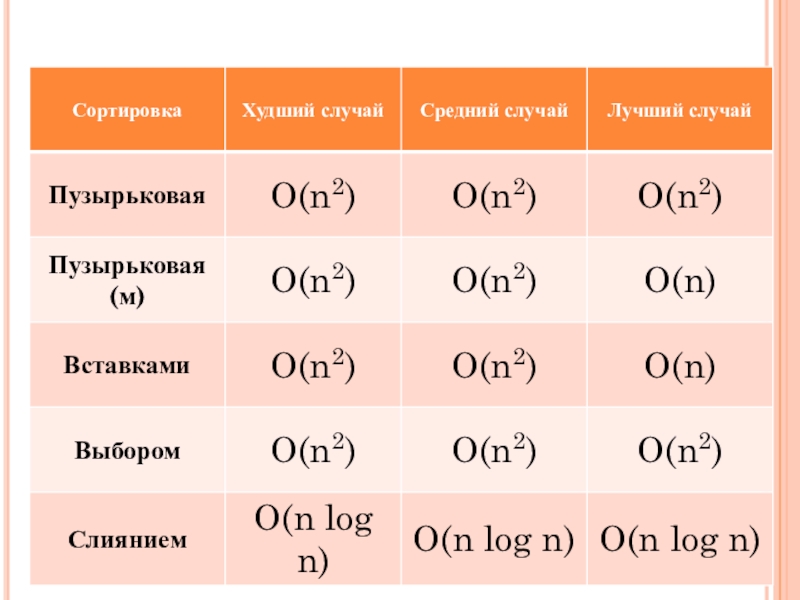
- 23. СРАВНИТЕЛЬНАЯ ТАБЛИЦА СОРТИРОВОК
В чем состоит задача сортировки?Зачем нужно изучать сортировку?Сортировка пузырькомСортировка выборомСортировка вставкамиСортировка слиянием
Слайд 1
ТЕМА УРОКА: «АЛГОРИТМЫ СОРТИРОВКИ»
Дисциплина ОП.08 Теория алгоритмов
Преподаватель Скряго О.С.
Смоленск 2014
Слайд 2В чем состоит задача сортировки?
Зачем нужно изучать сортировку?
Сортировка пузырьком
Сортировка выбором
Сортировка вставками
Сортировка
слиянием
Слайд 31. В ЧЕМ СОСТОИТ ЗАДАЧА СОРТИРОВКИ?
Сортировка – упорядочЕние заданного списка элементов.
Вход:
последовательность, состоящая из n чисел (a1, a2, …, an).
Выход: перестановка (изменение порядка) (a1’, a2’,…, an’) входной последовательности таким образом, что a1’ ≤ a2’ ≤ … ≤ an’.
Входная последовательность представляется в виде n-элементного массива.
Выход: перестановка (изменение порядка) (a1’, a2’,…, an’) входной последовательности таким образом, что a1’ ≤ a2’ ≤ … ≤ an’.
Входная последовательность представляется в виде n-элементного массива.
Слайд 41. В ЧЕМ СОСТОИТ ЗАДАЧА СОРТИРОВКИ?
Устойчивый алгоритм – не меняет относительное
расположение одинаковых элементов в массиве.
Если номера двух одинаковых элементов i < j, то в отсортированном списке i’ < j’
Обменный (in-place) алгоритм – для его работы не требуется дополнительная память, которая зависит от размера массива.
Если номера двух одинаковых элементов i < j, то в отсортированном списке i’ < j’
Обменный (in-place) алгоритм – для его работы не требуется дополнительная память, которая зависит от размера массива.
Слайд 51. В ЧЕМ СОСТОИТ ЗАДАЧА СОРТИРОВКИ?
Как правило, сортируются только ключи, которые
существуют в записях (строчка в таблице, список, объект)
Базовая операция – сравнение двух элементов: ai ≤ aj (кроме некоторых специальных алгоритмов)
Время работы: Ω(n log n)
Рассматривается сортировка по возрастанию
Базовая операция – сравнение двух элементов: ai ≤ aj (кроме некоторых специальных алгоритмов)
Время работы: Ω(n log n)
Рассматривается сортировка по возрастанию
Слайд 62. ЗАЧЕМ НУЖНО ИЗУЧАТЬ СОРТИРОВКУ?
Во многих приложениях нужно сортировать данные
Выдача информации
(отчеты, списки)
Сортировка для бинарного поиска
Геометрические алгоритмы (вывод графики, поиск выпуклой оболочки)
Многие алгоритмы требуют предварительную сортировку данных
Алгоритмы сортировки – прекрасный способ изучения алгоритмов (большое количество алгоритмов, много техник).
Сортировка для бинарного поиска
Геометрические алгоритмы (вывод графики, поиск выпуклой оболочки)
Многие алгоритмы требуют предварительную сортировку данных
Алгоритмы сортировки – прекрасный способ изучения алгоритмов (большое количество алгоритмов, много техник).
Слайд 83. СОРТИРОВКА ПУЗЫРЬКОМ
Суть алгоритма: многократный проход по списку и сравнение двух
соседних элементов. Если ai > ai+1, то элементы меняются местами.
На первом проходе в конец списка перемещается («всплывает») самый большой элемент, на втором проходе – всплывает второй по величине элемент и т.д.
На первом проходе в конец списка перемещается («всплывает») самый большой элемент, на втором проходе – всплывает второй по величине элемент и т.д.
Слайд 93. СОРТИРОВКА ПУЗЫРЬКОМ
Алгоритм Bubble sort (A[0…n-1])
for i=0 to n-2 do
for j=0 to n-2-i do
if A[j+1] < A[j]
обмен A[j] и A[j+1]
Время работы: O(n2)
Разные случаи: нет
Модификация: если при проходе нет обмена – список отсортирован
if A[j+1] < A[j]
обмен A[j] и A[j+1]
Время работы: O(n2)
Разные случаи: нет
Модификация: если при проходе нет обмена – список отсортирован
Слайд 114. СОРТИРОВКА ВЫБОРОМ
Суть алгоритма: проходим по списку, ищем наименьший элемент и
меняем местами с первым элементом. Далее находим второй наименьший элемент и меняем его местами со вторым элементом и т.д.
Есть другой вариант: ищем наибольший элемент и меняем местами с последним элементом.
Есть другой вариант: ищем наибольший элемент и меняем местами с последним элементом.
Слайд 124. СОРТИРОВКА ВЫБОРОМ
Алгоритм Selection sort (A[0…n-1])
for i=0 to n-2 do
min=i
for j=i+1 to n-1 do
if A[j] < A[min]
min=j
обмен A[j] и A[min]
Время работы: O(n2)
Разные случаи: нет
for j=i+1 to n-1 do
if A[j] < A[min]
min=j
обмен A[j] и A[min]
Время работы: O(n2)
Разные случаи: нет
Слайд 145. СОРТИРОВКА ВСТАВКАМИ
Суть алгоритма: делим список на отсортированную часть и неотсортированную.
Изначально в отсортированную часть попадает первое значение списка.
Далее сравниваем следующее значение со значениями в отсортированном списке и ставим его в нужном порядке, после чего отсортированная часть увеличивается на 1.
Потом берем следующее значение и т.д.
Слайд 155. СОРТИРОВКА ВСТАВКАМИ
Алгоритм Insertion sort (A[0…n-1])
for i=1 to n-1 do
v=A[i]
j=i-1
while j≥0 AND A[j]>v do
A[j+1]=A[j]
j=j-1
A[j+1]=v
j=i-1
while j≥0 AND A[j]>v do
A[j+1]=A[j]
j=j-1
A[j+1]=v
Слайд 165. СОРТИРОВКА ВСТАВКАМИ
Время работы: O(n2) в худшем случае, O(n) в лучшем
случае.
Разные случаи: да, зависит от характера входных данных. Чем ближе входные данные к отсортированным – тем меньше сравнений.
Разные случаи: да, зависит от характера входных данных. Чем ближе входные данные к отсортированным – тем меньше сравнений.
Слайд 186. СОРТИРОВКА СЛИЯНИЕМ
Суть алгоритма: список рекурсивно делится пополам, после чего каждая
половина рекурсивно сортируется, после чего две половины сливаются в один отсортированный массив.
Список рекурсивно делится пополам, пока все подмассивы не будут содержать 1 или 0 элементов.
Если сортируемый список нечетный – один из подмассивов будет пустым.
Список рекурсивно делится пополам, пока все подмассивы не будут содержать 1 или 0 элементов.
Если сортируемый список нечетный – один из подмассивов будет пустым.
Слайд 196. СОРТИРОВКА СЛИЯНИЕМ
Алгоритм Mergesort (A[0…n-1])
if n>1
Копировать A[0…n/2-1] в B[0…n/2-1]
Копировать A[n/2…n-1] в С[0…n/2-1]
Mergesort (B[0…n/2-1])
Mergesort (С[0…n/2-1])
Merge (B,C,A)
Mergesort (B[0…n/2-1])
Mergesort (С[0…n/2-1])
Merge (B,C,A)
Слайд 206. СОРТИРОВКА СЛИЯНИЕМ
Алгоритм Merge (B[0…p-1], C[0…q-1], A[0…p+q-1)
i=0; j=0; k=0
While i
j
if B[i]≤C[j]
A[k]=B[i]; i=i+1
else
A[k]=C[j]; j=j+1
k=k+1
if i=p
Копировать C[j…q-1] в A[k…p+q-1]
Else
Копировать B[i…p-1] в A[k…p+q-1]
Слайд 226. СОРТИРОВКА СЛИЯНИЕМ
Время работы: O(n log n) в худшем случае, O(n
log n) в лучшем случае.
Разные случаи: да, зависит от характера входных данных, но не значительно
Требует n дополнительной памяти для подмассивов
Разные случаи: да, зависит от характера входных данных, но не значительно
Требует n дополнительной памяти для подмассивов








![Презентация по теме Алгоритмы сортировки для дисциплины ОП.08 Теория алгоритмов 3. СОРТИРОВКА ПУЗЫРЬКОМАлгоритм Bubble sort (A[0…n-1])for i=0 to n-2 do for 3. СОРТИРОВКА ПУЗЫРЬКОМАлгоритм Bubble sort (A[0…n-1])for i=0 to n-2 do for j=0 to n-2-i do](/img/thumbs/bac1f8e4c39b85e7481504f40c307758-800x.jpg)


![Презентация по теме Алгоритмы сортировки для дисциплины ОП.08 Теория алгоритмов 4. СОРТИРОВКА ВЫБОРОМАлгоритм Selection sort (A[0…n-1])for i=0 to n-2 do min=i 4. СОРТИРОВКА ВЫБОРОМАлгоритм Selection sort (A[0…n-1])for i=0 to n-2 do min=i for j=i+1 to n-1](/img/thumbs/b28c2b430321c3c74c6379f52fdf3151-800x.jpg)


![Презентация по теме Алгоритмы сортировки для дисциплины ОП.08 Теория алгоритмов 5. СОРТИРОВКА ВСТАВКАМИАлгоритм Insertion sort (A[0…n-1])for i=1 to n-1 do v=A[i] 5. СОРТИРОВКА ВСТАВКАМИАлгоритм Insertion sort (A[0…n-1])for i=1 to n-1 do v=A[i] j=i-1 while j≥0](/img/thumbs/a1a8a46028dfd10689b60ffddffc19d4-800x.jpg)



![Презентация по теме Алгоритмы сортировки для дисциплины ОП.08 Теория алгоритмов 6. СОРТИРОВКА СЛИЯНИЕМАлгоритм Mergesort (A[0…n-1])if n>1 Копировать A[0…n/2-1] в B[0…n/2-1] Копировать 6. СОРТИРОВКА СЛИЯНИЕМАлгоритм Mergesort (A[0…n-1])if n>1 Копировать A[0…n/2-1] в B[0…n/2-1] Копировать A[n/2…n-1] в С[0…n/2-1]](/img/thumbs/5cf03301b1d74af210a9d3f9b29e25c8-800x.jpg)
![Презентация по теме Алгоритмы сортировки для дисциплины ОП.08 Теория алгоритмов 6. СОРТИРОВКА СЛИЯНИЕМАлгоритм Merge (B[0…p-1], C[0…q-1], A[0…p+q-1)i=0; j=0; k=0While i 6. СОРТИРОВКА СЛИЯНИЕМАлгоритм Merge (B[0…p-1], C[0…q-1], A[0…p+q-1)i=0; j=0; k=0While i](/img/thumbs/0febeb30603ec6d8f96da5914c08c137-800x.jpg)