- учитель информатики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по межпредметным задачам в информатике
Содержание
- 1. Презентация по межпредметным задачам в информатике
- 2. Уровни межпредметных заданийИсследовательскиеСистематизация, анализ и синтез;Формирование предметной
- 3. Задачи, развивающие нестандартное мышлениеСоставить из 6 спичек
- 4. Задачи, развивающие нестандартное мышлениеНа столе лежит замкнутая
- 5. Логические задачи в информатикеЯ проигралЯ не проигралЯ не выигралЯ выигралДелим кушЯ не знаю
- 6. Таблицы истинностиДима занимается карате, Петр никогда не
- 7. Задачи с кодированием информацииЗадача на «информационный обрыв»
- 8. Пример построения графика функцииГрафик функциизатруднительно построить с применением схемы исследования
- 9. Построение графиков функций одной переменнойОписаниеПостроение графиков средствами
- 10. Построение графиков функций одной переменнойПреимуществаМожно строить графики
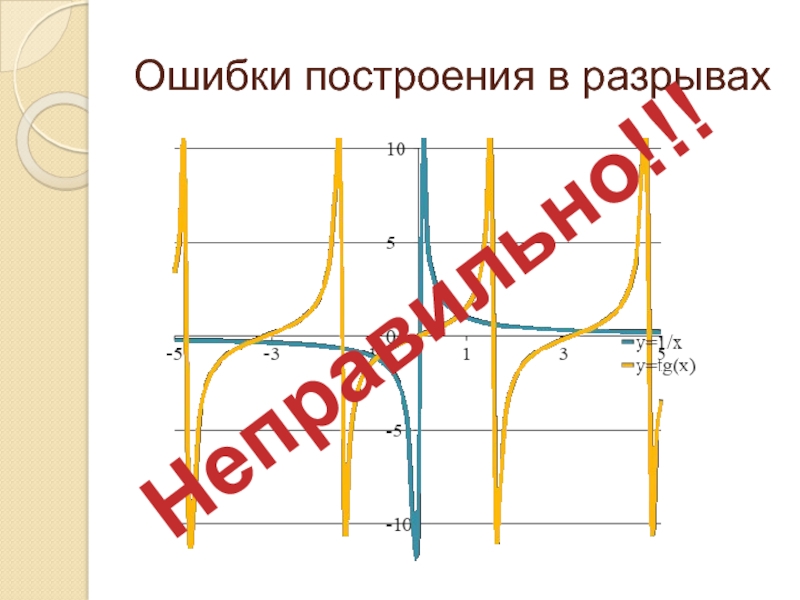
- 11. Ошибки построения в разрывахНеправильно!!!
- 12. Построение кривых заданных параметрическим способом
- 13. Объемные фигуры (программирование)Преобразования в различных системах координатРазвитие пространственного видения
- 14. ЗадачаРешить уравнение
- 15. Рассмотрим функцию.Область определения
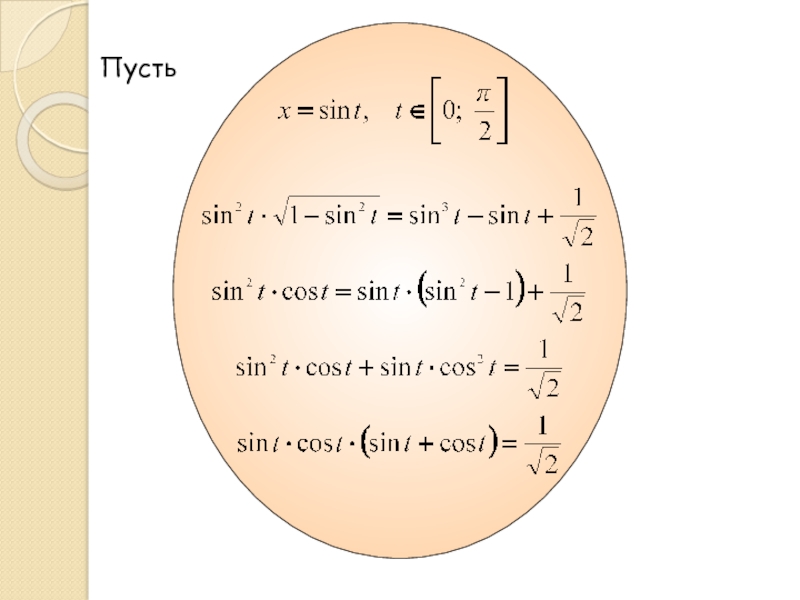
- 16. Пусть
- 17. Пусть
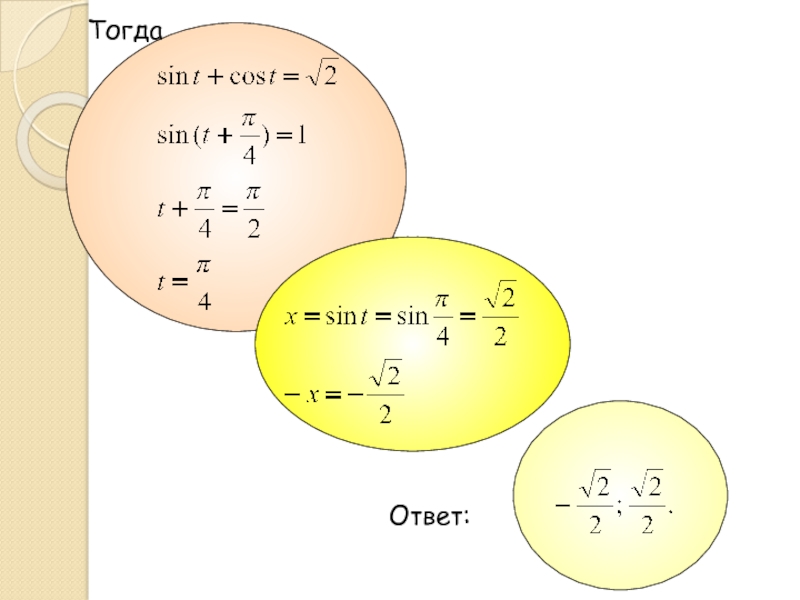
- 18. ТогдаОтвет:
- 19. Решение задач подбором параметровМетод позволяет найти один
- 20. Решение задач подбором параметровПреимущества:Можно находить приближенные значения
- 21. Элементы дифференциального и интегрального исчисленияИзвестно, что определенный
- 22. Геометрический метод Вычислить интеграл-2
- 23. Вычисление определенных интегралов и производныхПлощадь криволинейной трапеции
- 24. Спасибо за вниманиеВся природа и искусство –
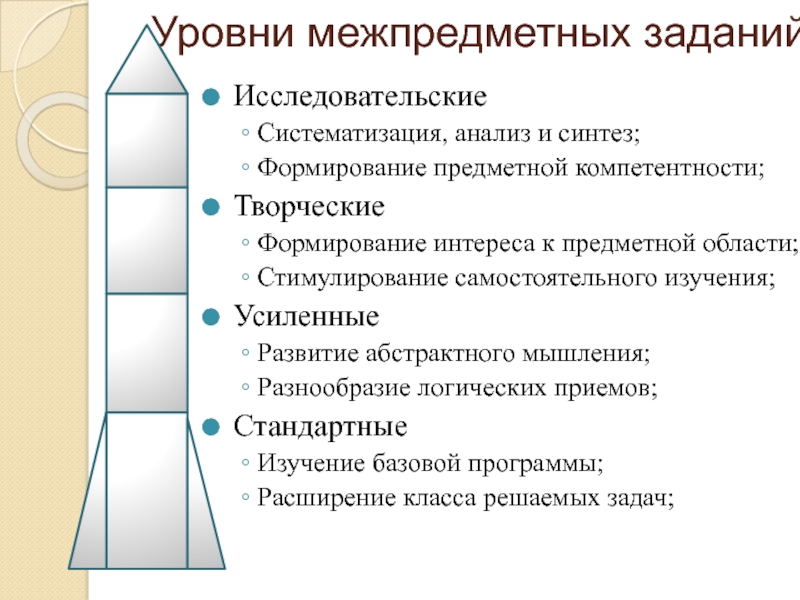
Уровни межпредметных заданийИсследовательскиеСистематизация, анализ и синтез;Формирование предметной компетентности;ТворческиеФормирование интереса к предметной области;Стимулирование самостоятельного изучения;УсиленныеРазвитие абстрактного мышления; Разнообразие логических приемов;СтандартныеИзучение базовой программы;Расширение класса решаемых задач;
Слайд 1Шевчук Н.М. - учитель математики
Гимназия №1 им. К.Д.Ушинского г. Симферополя
+мате
инфор
матика
Чайка К.В.
Слайд 2Уровни межпредметных заданий
Исследовательские
Систематизация, анализ и синтез;
Формирование предметной компетентности;
Творческие
Формирование интереса к предметной
области;
Стимулирование самостоятельного изучения;
Усиленные
Развитие абстрактного мышления;
Разнообразие логических приемов;
Стандартные
Изучение базовой программы;
Расширение класса решаемых задач;
Стимулирование самостоятельного изучения;
Усиленные
Развитие абстрактного мышления;
Разнообразие логических приемов;
Стандартные
Изучение базовой программы;
Расширение класса решаемых задач;
Слайд 3Задачи, развивающие нестандартное мышление
Составить из 6 спичек 4 равносторонних треугольника
Задано число
81**. Вместо звездочек вставить цифры так, чтобы полученное число делилось на 45
Слайд 4Задачи, развивающие нестандартное мышление
На столе лежит замкнутая цепь, состоящая из 2013
одинаковых шестеренок. Одну из них поворачивают. Будет ли цепь подвижной.
Слайд 5Логические задачи в информатике
Я проиграл
Я не проиграл
Я не выиграл
Я выиграл
Делим куш
Я
не знаю
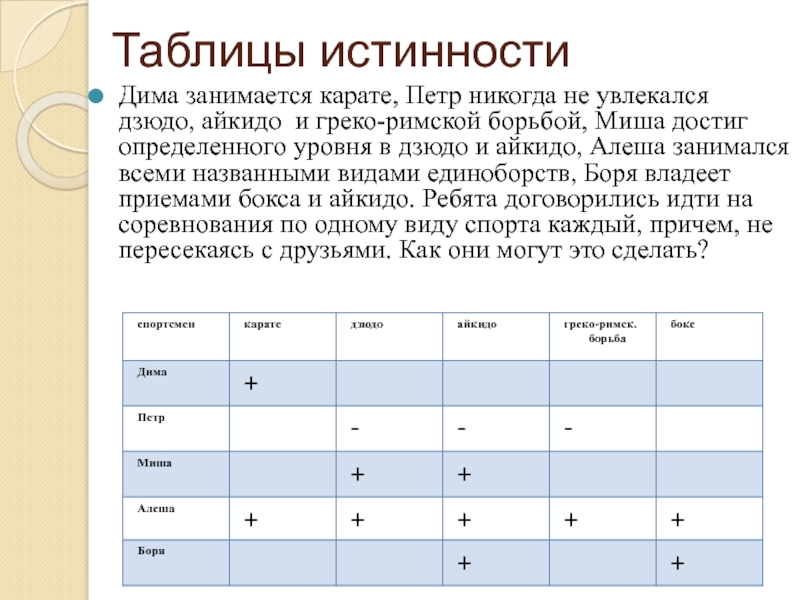
Слайд 6Таблицы истинности
Дима занимается карате, Петр никогда не увлекался дзюдо, айкидо и
греко-римской борьбой, Миша достиг определенного уровня в дзюдо и айкидо, Алеша занимался всеми названными видами единоборств, Боря владеет приемами бокса и айкидо. Ребята договорились идти на соревнования по одному виду спорта каждый, причем, не пересекаясь с друзьями. Как они могут это сделать?
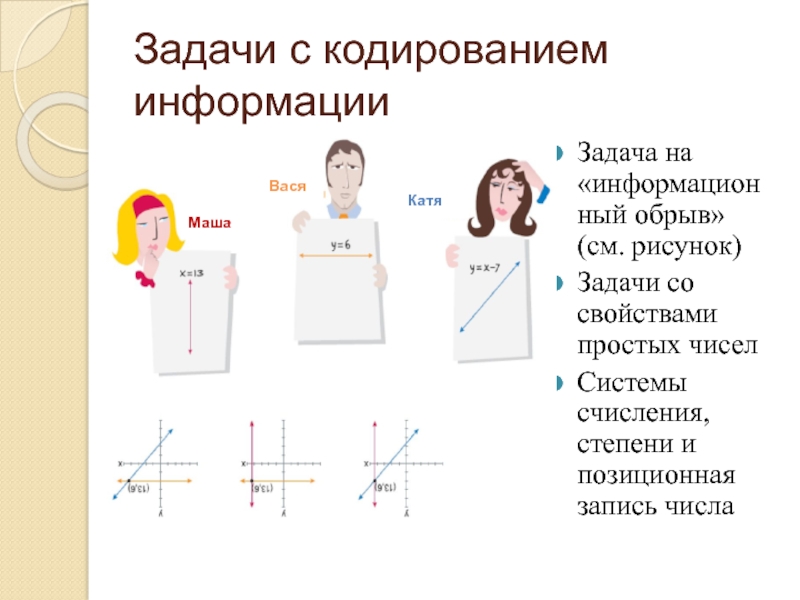
Слайд 7Задачи с кодированием информации
Задача на «информационный обрыв» (см. рисунок)
Задачи со свойствами
простых чисел
Системы счисления, степени и позиционная запись числа
Системы счисления, степени и позиционная запись числа
Маша
Вася
Катя
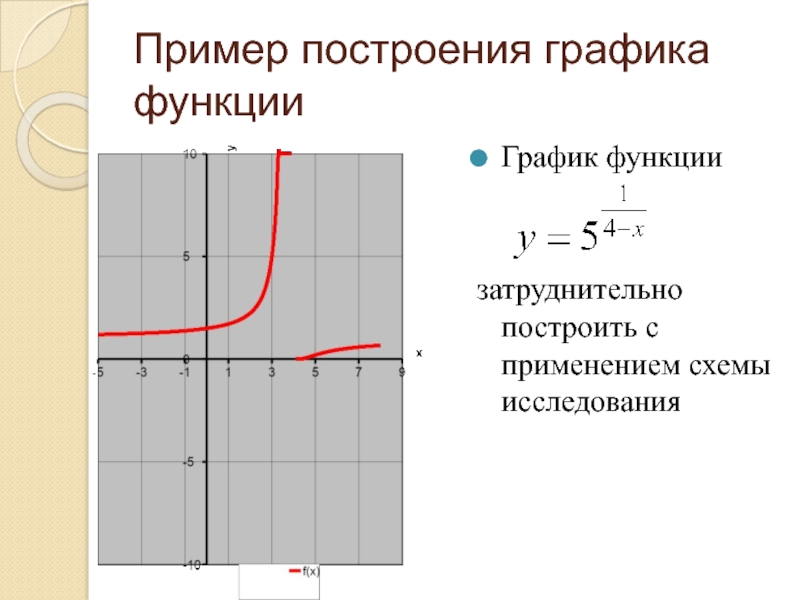
Слайд 8Пример построения графика функции
График функции
затруднительно построить с применением схемы исследования
Слайд 9Построение графиков функций одной переменной
Описание
Построение графиков средствами табличного процессора значительно отличается
от построения с использованием схемы исследования функции на уроке математики. Метод заключается в разбиении области построения на достаточно большое число точек
в каждой из которых вычисляется значение функции f(x)
после чего точки наносятся на плоскость и соединяются гладкими непрерывными кривыми.
в каждой из которых вычисляется значение функции f(x)
после чего точки наносятся на плоскость и соединяются гладкими непрерывными кривыми.
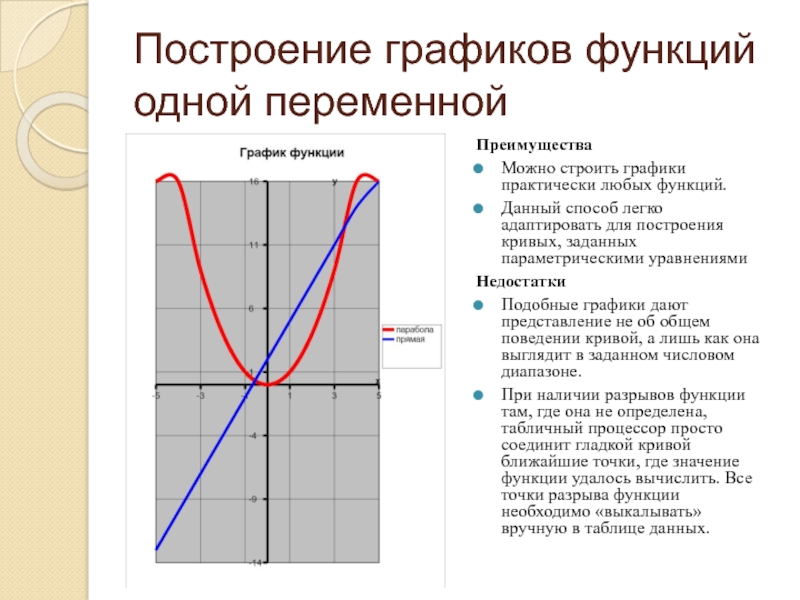
Слайд 10Построение графиков функций одной переменной
Преимущества
Можно строить графики практически любых функций.
Данный способ
легко адаптировать для построения кривых, заданных параметрическими уравнениями
Недостатки
Подобные графики дают представление не об общем поведении кривой, а лишь как она выглядит в заданном числовом диапазоне.
При наличии разрывов функции там, где она не определена, табличный процессор просто соединит гладкой кривой ближайшие точки, где значение функции удалось вычислить. Все точки разрыва функции необходимо «выкалывать» вручную в таблице данных.
Недостатки
Подобные графики дают представление не об общем поведении кривой, а лишь как она выглядит в заданном числовом диапазоне.
При наличии разрывов функции там, где она не определена, табличный процессор просто соединит гладкой кривой ближайшие точки, где значение функции удалось вычислить. Все точки разрыва функции необходимо «выкалывать» вручную в таблице данных.
Слайд 13Объемные фигуры (программирование)
Преобразования в различных системах координат
Развитие пространственного видения
Слайд 15Рассмотрим функцию.
Область определения
симметричная относительно начала координат и
тогда – чётная по определению. Следовательно, можно искать решение ( 1 ) на интервале .
тогда – чётная по определению. Следовательно, можно искать решение ( 1 ) на интервале .
Слайд 19Решение задач подбором параметров
Метод позволяет найти один произвольный корень уравнения вида:
Математическая сущность этого численного метода проста. На числовой прямой перебором значений находятся точки x1 и x2 , такие что:
затем интервал сужается методом деления пополам до достижения приближенного равенства .
Слайд 20Решение задач подбором параметров
Преимущества:
Можно находить приближенные значения корней, получение которых аналитическим
способом весьма затруднительно.
Недостатки:
Находит лишь ОДНО решение (либо позволяет сделать вывод, что корней нет), то есть, строго говоря, НЕ РЕШАЕТ уравнение.
Недостатки:
Находит лишь ОДНО решение (либо позволяет сделать вывод, что корней нет), то есть, строго говоря, НЕ РЕШАЕТ уравнение.
Пример:
x17-5x9+7x8-x2+2cos(x)=10
Слайд 21Элементы дифференциального и интегрального исчисления
Известно, что определенный интеграл функции y=f(x)
численно представляет собой площадь криволинейной трапеции S, ограниченной кривыми:
y=0, x=a, x=b и y=f(x).
В случаях, когда функцию затруднительно проинтегрировать аналитическим путем, можно воспользоваться численными методами.
<=Вычисление производной
Слайд 23Вычисление определенных интегралов и производных
Площадь криволинейной трапеции S приближенно можно вычислить,
сведя ее к нескольким прямолинейным трапециям. Для этого разобьем отрезок [a; b] на n равных частей. Очевидно, что чем мельче будет разбиение отрезка [a; b], тем ближе будет площадь S к сумме площадей Σ Si . Каждая из площадей этих прямолинейных трапеций рассчитывается по формуле
Слайд 24Спасибо за внимание
Вся природа и искусство – это целесообразно и гармонично
устроенное целое. И в природе и в искусстве отдельные вещи и явления существуют как часть целого, как момент в общей системе красоты и гармонии.