- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Алгебра высказываний (10 класс)
Содержание
- 1. Презентация по информатике на тему Алгебра высказываний (10 класс)
- 2. Алгебра высказываний (алгебра логики) -это математический
- 3. Логическая переменная это простое высказывание, содержащее только
- 4. составное высказывание, содержит несколько простых высказываний, соединенных между собой с помощью логических операций
- 5. Рассмотрим два простых высказыванияА=«Число 10-четное», В=«Число 10
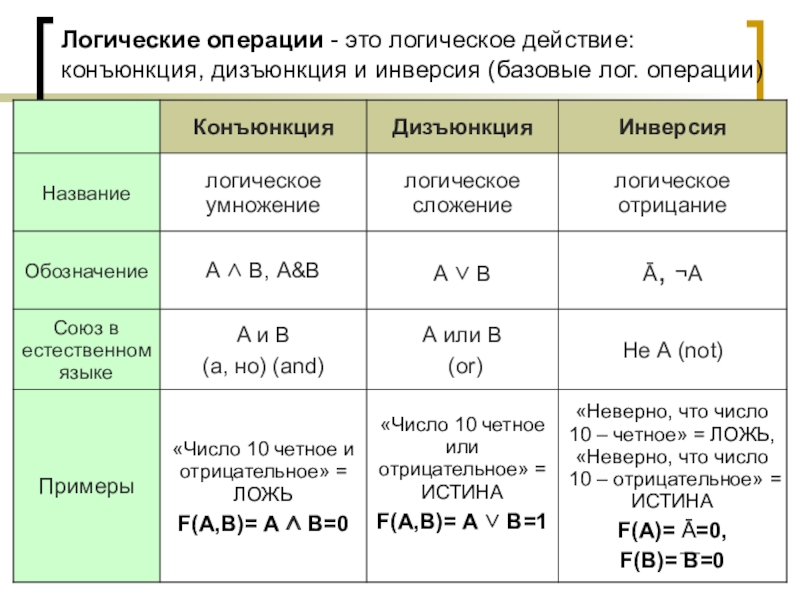
- 6. Логические операции - это логическое действие: конъюнкция, дизъюнкция и инверсия (базовые лог. операции)
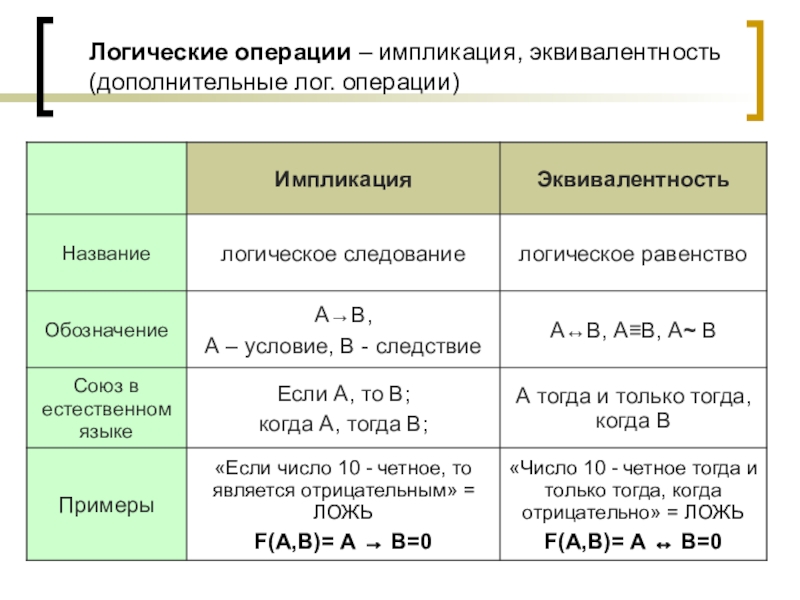
- 7. Логические операции – импликация, эквивалентность (дополнительные лог. операции)
- 8. Таблица истинности -таблица, определяющая значение сложного высказывания при всех возможных значениях простых высказываний
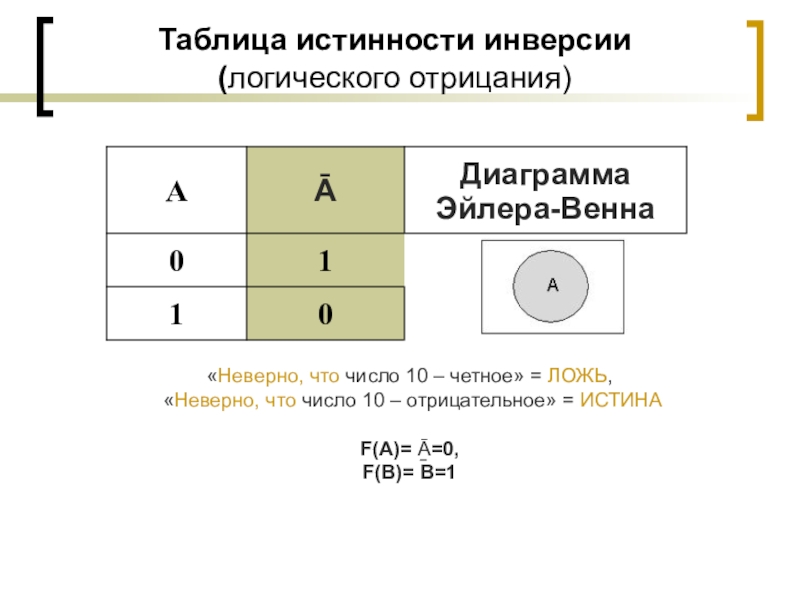
- 9. Таблица истинности инверсии (логического отрицания)«Неверно, что число
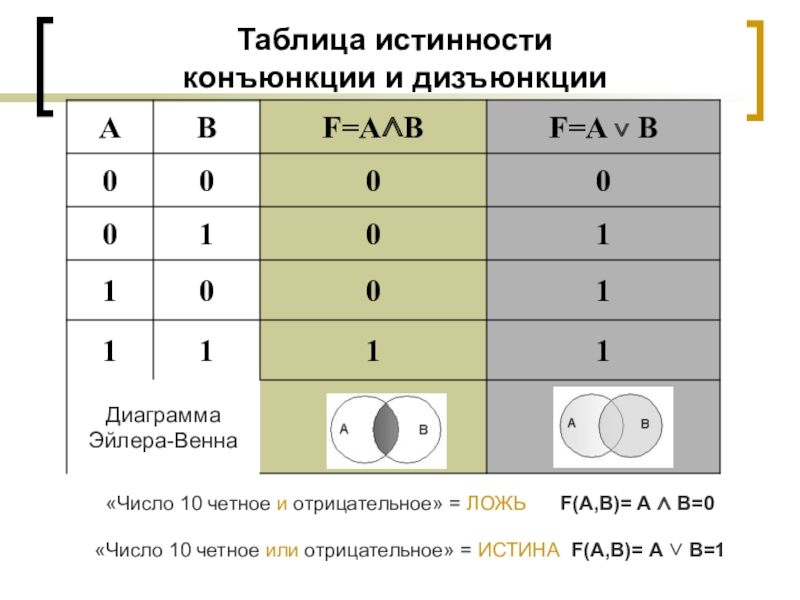
- 10. Таблица истинности конъюнкции и дизъюнкции «Число
- 11. Таблица истинности импликации и эквивалентности«Если число
- 12. Примеры импликацииа) { Если 2x2 = 4,
- 13. Примеры эквивалентностиРассмотрим возможные значения сложного высказывания, являющегося
- 14. РЕШИМ ЗАДАЧИ:Определите, в каком порядке необходимо вычислять
- 15. Вычисление логических выраженийПример1. Вычислить значение логического выражения
- 16. Задание 2. Определите истинность составного высказывания
- 17. Задание 3. Найти значения логического выражения:1)2)3)4) (0V1)→(1&1)=1→1=15) (1&1V0)↔(¬1&1)=1↔0 =06) ¬((1→0)↔(1&1)V1)= ¬(0↔1)= ¬0= 1
- 18. ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ ПО ЛОГИЧЕСКОМУ ВЫРАЖЕНИЮТаблицу, показывающую,
- 19. Порядок действий: Количество строк в таблице Q=2n,
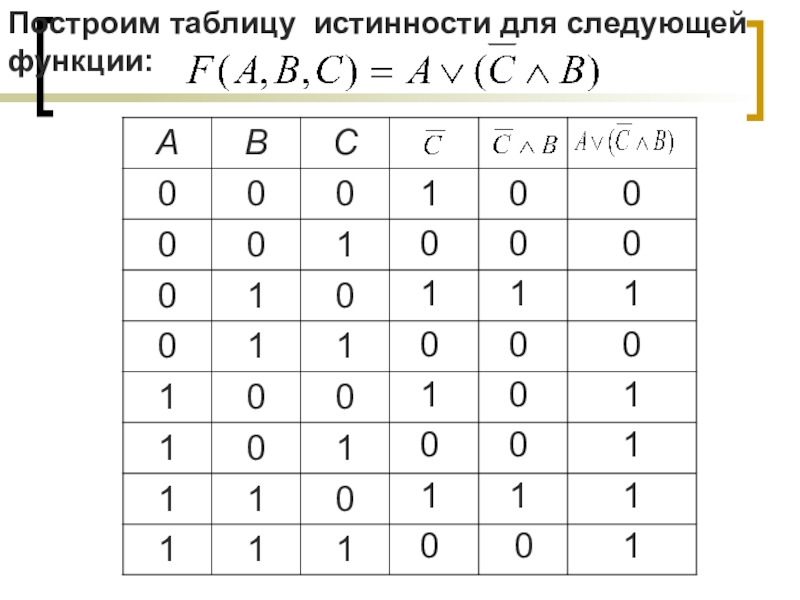
- 20. Построим таблицу истинности для следующей функции: 111100000010001000101111
- 21. Задание. Построить таблицу истинности для следующих функций: 00111010011010001010101001
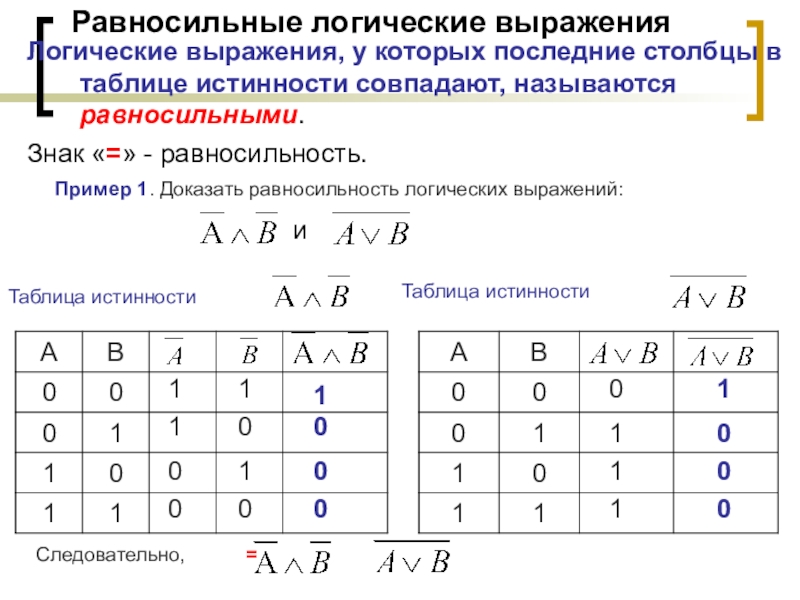
- 22. Равносильные логические выраженияЛогические выражения, у которых последние
- 23. Записать составное выражение «(2·2=4 и 3·3=9)
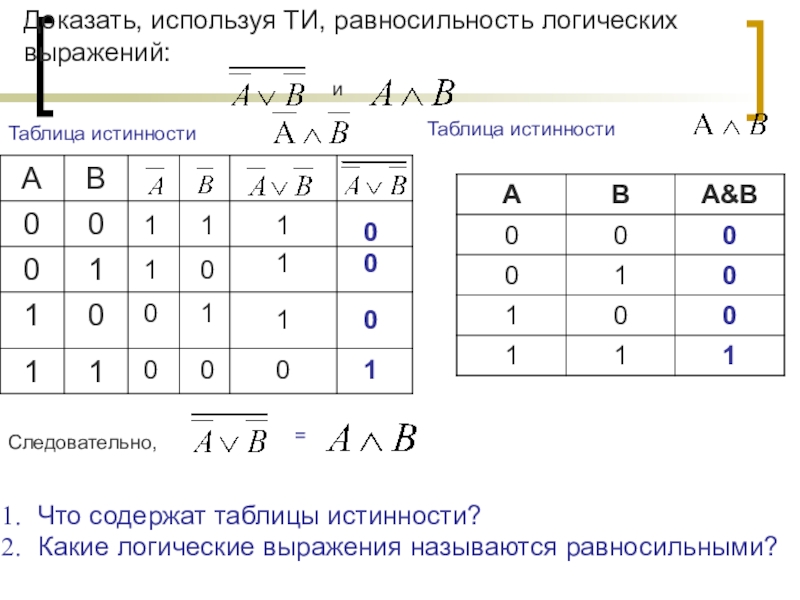
- 24. Доказать, используя ТИ, равносильность логических выражений:0111001000011110Что содержат таблицы истинности?Какие логические выражения называются равносильными?
Слайд 2Алгебра высказываний
(алгебра логики) -
это математический аппарат, с помощью которого записывают,
логические высказывания.
Создателем математической логики является живший в ХIХ веке английский математик Джордж Буль, в честь которого эта алгебра названа булевой алгеброй высказываний или алгеброй логики.
В 20 веке алгебра логики стала математическим основанием работы ПК.
Слайд 3Логическая переменная
это простое высказывание, содержащее только одну мысль.
Ее символическое обозначение
Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0).
Пример:
А=“6 — четное число”, A=1
D=“Рим — столица Франции”, D=0
Слайд 4составное высказывание, содержит несколько простых высказываний, соединенных между собой с помощью
Слайд 5
Рассмотрим два простых высказывания
А=«Число 10-четное»,
В=«Число 10 –отрицательное»
В нашем случае первое
Слайд 6Логические операции - это логическое действие: конъюнкция, дизъюнкция и инверсия (базовые
Слайд 8Таблица истинности -
таблица, определяющая значение сложного высказывания при всех возможных значениях
Слайд 9Таблица истинности инверсии (логического отрицания)
«Неверно, что число 10 – четное» =
«Неверно, что число 10 – отрицательное» = ИСТИНА
F(A)= Ā=0,
F(B)= B=1
Слайд 10Таблица истинности
конъюнкции и дизъюнкции
«Число 10 четное и отрицательное» =
«Число 10 четное или отрицательное» = ИСТИНА F(A,B)= А ∨ В=1
Слайд 11Таблица истинности
импликации и эквивалентности
«Если число 10 - четное, то является
F(A,B)= А → В=0
«Число 10 - четное тогда и только тогда, когда отрицательно» = ЛОЖЬ
F(A,B)= А ↔ В=0
Слайд 12Примеры импликации
а) { Если 2x2 = 4, то через Смоленск протекает
б) {Если через Смоленск протекает Енисей, то 2x2 = 4}
в) {Если через Смоленск протекает Енисей, то 2x2 = 5}
г) {Если все ученики класса напишут контрольную работу по физике на отлично, то слоны в Африке живут}
д) {Если через Смоленск протекает Енисей, то все ученики класса напишут контрольную работу по физике на отлично}
е) {Если 2 х 2 = 4, то через Смоленск протекает Енисей}
ж) {Если через Смоленск протекает Днепр, то Луна сделана из теста}
Слайд 13Примеры эквивалентности
Рассмотрим возможные значения сложного высказывания, являющегося эквивалентностью:
{Учитель утверждает, что
а) Ученик получил 5 на зачете и 5 в четверти
б) Ученик не получил на зачете 5, и учитель не поставил ему 5 в четверти
в) Ученик не получил на зачете 5, но учитель поставил ему 5 в четверти
г) Ученик получил 5 на зачете, но учитель не поставил ему 5 в четверти
Слайд 14РЕШИМ ЗАДАЧИ:
Определите, в каком порядке необходимо вычислять значение логического выражения:
1) ¬
2) A & (B & C)
3) (A & B) ν (C & ¬ D)
4) A ν ¬ D ν B
5) A → (B ↔ ¬ A)
1
2
3
1
2
1
2
3
4
1
2
1
2
3
3
Приоритет логических операций:
() Операции в скобках
НЕ Отрицание
И логическое умножение
ИЛИ Логическое сложение
→ Импликация
↔ Эквивалентность
Слайд 15Вычисление логических выражений
Пример1.
Вычислить значение логического выражения
«(2·2=5 или 2·2=4}) и
Обозначим
А=«2·2=5» – ложно (0)
В=«2·2=4» – истинно (1)
Тогда (А или В) и ( или )
Слайд 16Задание 2. Определите истинность составного высказывания
А={Принтер – устройство вывода информации}
В={Процессор – устройство хранения информации}
C={Монитор – устройство вывода информации}
D={Клавиатура – устройство обработки информации}
Определяем истинность составного высказывания:
А=1, В=0, С=1, D=0
Установим истинность простых высказываний:
Слайд 17Задание 3. Найти значения логического выражения:
1)
2)
3)
4) (0V1)→(1&1)=
1→1=
1
5) (1&1V0)↔(¬1&1)=
1↔0 =
0
6) ¬((1→0)↔(1&1)V1)=
¬(0↔1)=
1
Слайд 18ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ
ПО ЛОГИЧЕСКОМУ ВЫРАЖЕНИЮ
Таблицу, показывающую, какие значения принимает сложное
По формуле логической функции легко рассчитать ее таблицу истинности, соблюдая приоритет логических операций и действия в скобках
Слайд 19Порядок действий:
Количество строк в таблице Q=2n, где n - количество
2. Количество столбцов = число переменных + число операций (здесь 3+3=6 столбцов)
3. Выписать наборы входных переменных. Это удобнее сделать так:
разделить колонку значений первой переменной пополам и заполнить верхнюю половину 0, нижнюю половину 1.
разделить колонку значений второй переменной на 4 части и заполнить каждую четверть чередующимися группами 0 и 1 , начиная опять с группы 0.
продолжить деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами из 0 или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа. (Можно заполнять все колонки, начиная с группы единиц.)
4. Провести заполнение таблицы истинности по столбикам, выполняя логические операции.
Пример. Построим таблицу истинности следующей функции:
Слайд 22Равносильные логические выражения
Логические выражения, у которых последние столбцы в таблице истинности
Знак «=» - равносильность.
и
0
1
1
1
1
0
1
0
0
0
0
0
0
1
1
1
1
0
0
0
Слайд 23 Записать составное выражение
«(2·2=4 и 3·3=9) или (2·2≠4 и 3·3≠9)»
А =«2·2=4» - 1 В = «3·3=9» - 1. Тогда
1
0
0
0
0
1
1
0
1
0
0
1
1
0
0
0
1
0
0
0