Евклида;
♦ описание алгоритма Евклида блок-схемой;
♦ программа на AЯ и на Паскале.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике 9 класс по теме: Алгоритм Евклида.
Содержание
- 1. Презентация по информатике 9 класс по теме: Алгоритм Евклида.
- 2. Наибольший общий делительРассмотрим следующую задачу: требуется составить программу определения
- 3. Идея алгоритма ЕвклидаИдея этого алгоритма основана на том свойстве,
- 4. Для «ручного» счета алгоритм Евклида выглядит так:1)
- 5. Описание алгоритма Евклида блок-схемойСтруктура алгоритма — цикл-пока
- 6. Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл
- 7. Программа на АЯ и на Паскале
- 8. Задание:Выполнить трассировку алгоритма Евклида для чисел: 36 и 42. (на оценку)!!!Д.з. § 40
Наибольший общий делительРассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел.Вспомним математику. Наибольший общий делитель двух натуральных чисел — это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12
Слайд 2Наибольший общий делитель
Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД)
двух натуральных чисел.
Вспомним математику. Наибольший общий делитель двух натуральных чисел — это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
НOД(12, 18) = 6.
Обозначим исходные данные как М и N. Постановка задачи выглядит следующим образом:
Дано: М, N Найти: НОД(M, N).
В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.
Вспомним математику. Наибольший общий делитель двух натуральных чисел — это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
НOД(12, 18) = 6.
Обозначим исходные данные как М и N. Постановка задачи выглядит следующим образом:
Дано: М, N Найти: НОД(M, N).
В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.
Слайд 3Идея алгоритма Евклида
Идея этого алгоритма основана на том свойстве, что если М>N, то
НОД(М,
N) = НОД(М – N, N).
Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.
Легко доказать это свойство. Пусть К — общий делитель М и N (М > N). Это значит, что М = mК, N = nК, где m,n — натуральные числа, причем m > n. Тогда М - N = К(m - n), откуда следует, что К — делитель числа М - N. Значит, все общие делители чисел М и N являются делителями их разности М - N в том числе и наибольший общий делитель.
Второе очевидное свойство:
НОД(М, М) = М.
Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.
Легко доказать это свойство. Пусть К — общий делитель М и N (М > N). Это значит, что М = mК, N = nК, где m,n — натуральные числа, причем m > n. Тогда М - N = К(m - n), откуда следует, что К — делитель числа М - N. Значит, все общие делители чисел М и N являются делителями их разности М - N в том числе и наибольший общий делитель.
Второе очевидное свойство:
НОД(М, М) = М.
Слайд 4Для «ручного» счета алгоритм Евклида выглядит так:
1) если числа равны, то
взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма;
2) затенить большее число разностью большего и меньшего из чисел;
3) вернуться к выполнению п. 1.
Рассмотрим этот алгоритм на примере М=32, N=24:
Получили: НОД(32, 24) = НОД(8, 8) = 8, что верно.
Рассмотрим этот алгоритм на примере М=32, N=24:
Получили: НОД(32, 24) = НОД(8, 8) = 8, что верно.
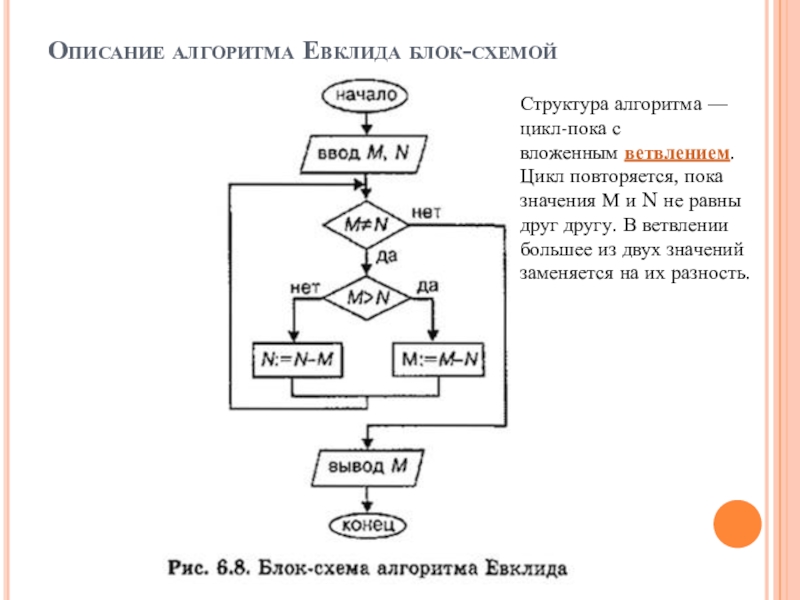
Слайд 5Описание алгоритма Евклида блок-схемой
Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется,
пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.
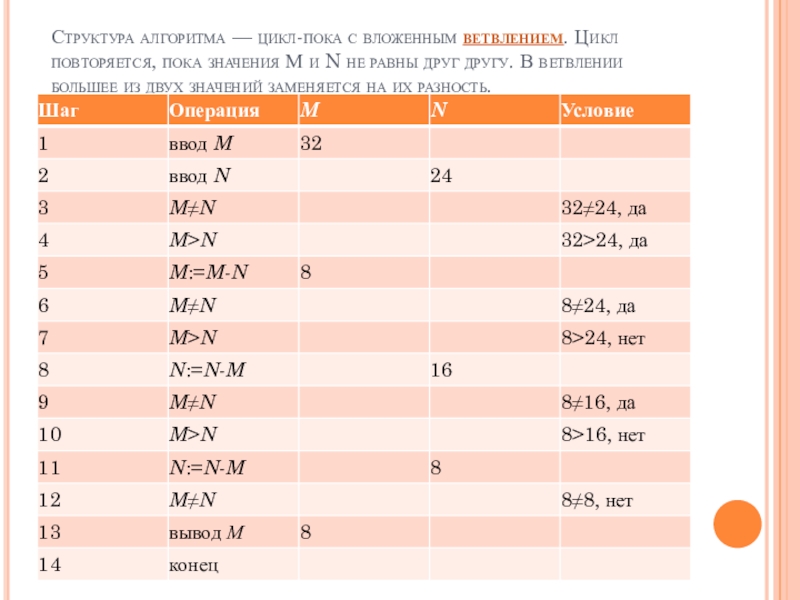
Слайд 6Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М
и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.