Презентация, доклад к уроку Основы логики

Содержание

1. Презентация к уроку Основы логики
2. Отцом алгебры логики по праву считается английский
3. Логическое высказывание – это повествовательное предложение, про
4. Составное высказывание – логическая функция, которая содержит несколько простых
5. А={Луна – планета}; В={2*2=4}; Простые высказыванияЛюбое высказывание либо истинно (1), либо ложно (0)
6. А={Луна – планета}; В={2*2=4}; А или В
7. Таблицы истинности – таблицы, в которых по действиям показано,
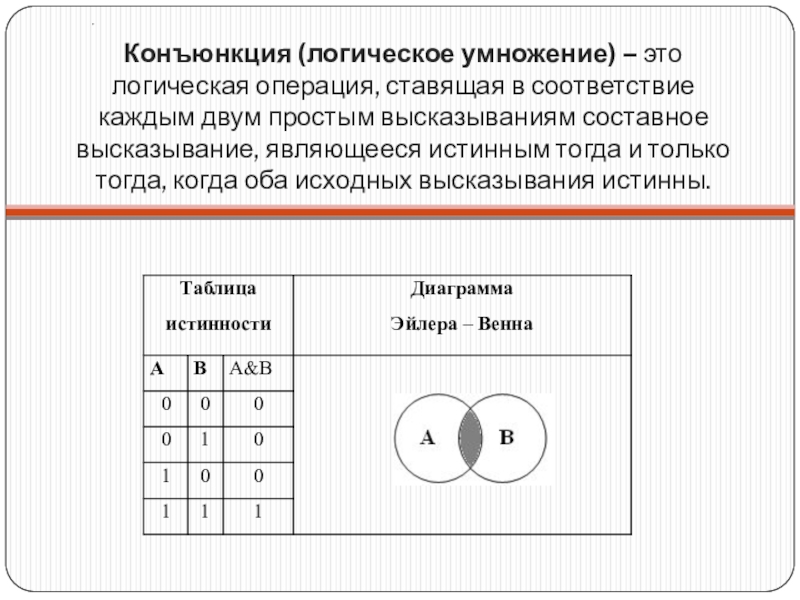
8. Конъюнкция (логическое умножение) – это логическая операция, ставящая в
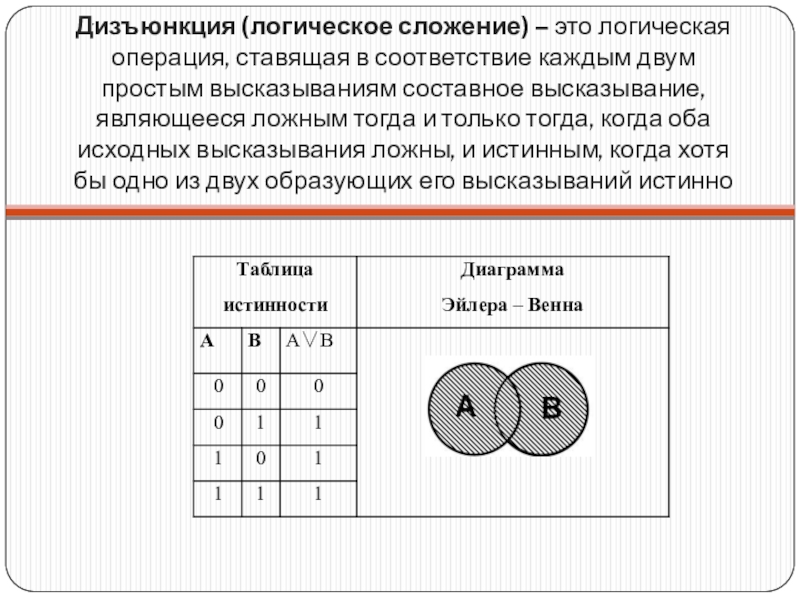
9. Дизъюнкция (логическое сложение) – это логическая операция, ставящая в
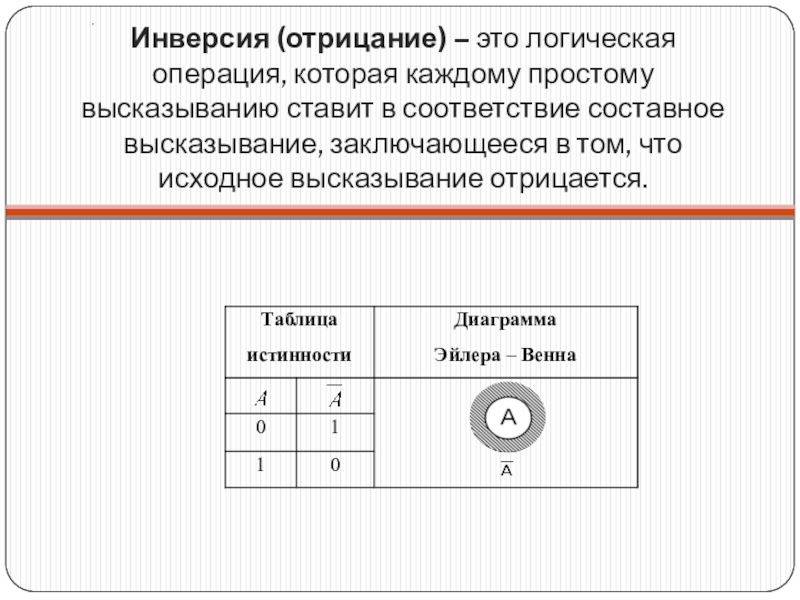
10. Инверсия (отрицание) – это логическая операция, которая каждому простому
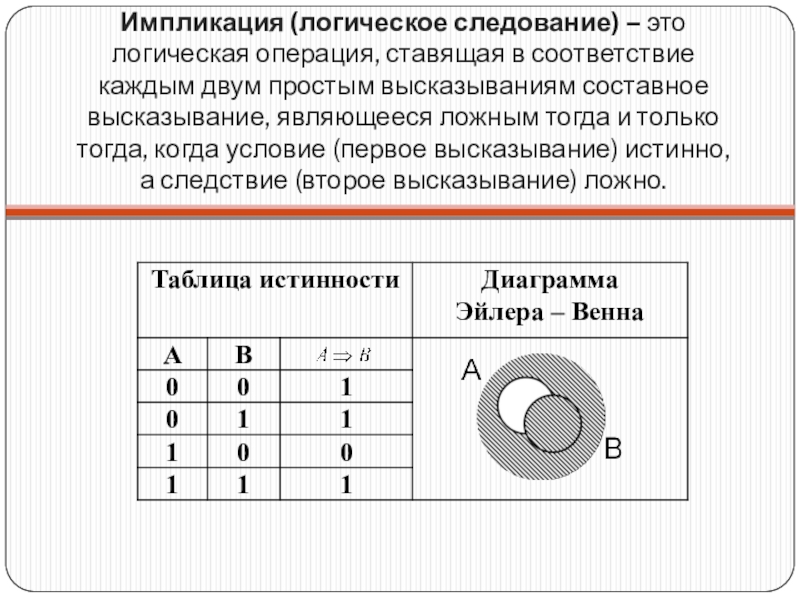
11. Импликация (логическое следование) – это логическая операция, ставящая в
12. При составлении логического выражения необходимо учитывать порядок
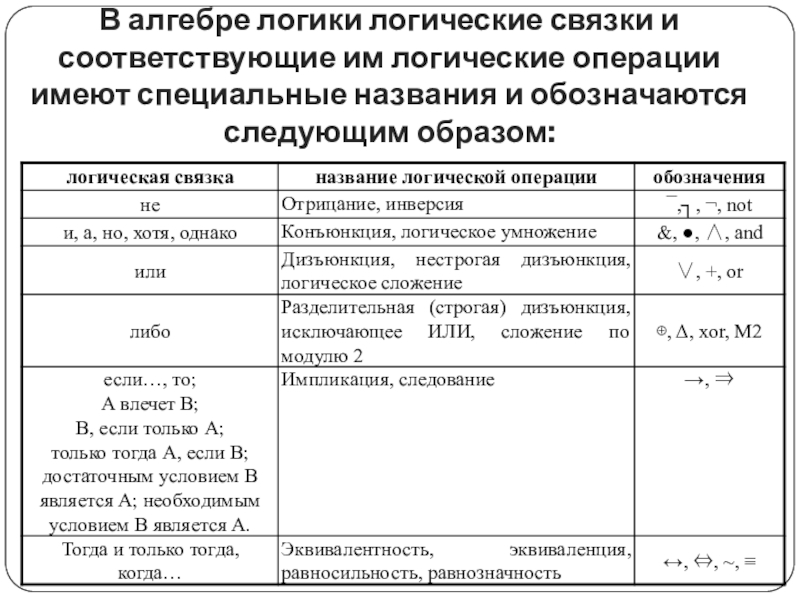
13. В алгебре логики логические связки и соответствующие
14. Запись импликации с помощью инверсии, конъюнкции и
15. Иногда при решении задач полезны формулы де

Отцом алгебры логики по праву считается английский математик XIX столетия Джордж Буль (1815 – 1864). В его честь алгебра логики названа булевой алгеброй высказыванийАлгебра логики изучает строение (форму структуру) сложных логических высказываний и способы установления их

Главная
Информатика
Презентация к уроку Основы логики

Слайд 1Шабалдина Н. В.
Основы алгебры логики

Слайд 2Отцом алгебры логики по праву считается английский математик XIX столетия Джордж

Буль (1815 – 1864). В его честь алгебра логики названа булевой алгеброй высказываний

Алгебра логики изучает строение (форму структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.

Отцом алгебры логики по праву считается английский математик XIX столетия Джордж Буль (1815 – 1864). В его

Слайд 3Логическое высказывание – это повествовательное предложение, про которое однозначно можно сказать:

истинно оно или ложно

Будут ли высказыванием следующие предложения?

Пятью пять – двадцать пять.
Пекин – столица Японии.
Информатика – любимый предмет.
Х+3=5
Победа!
Который час?
Ты сегодня пойдёшь в школу?

Слайд 4Составное высказывание – логическая функция, которая содержит несколько простых мыслей, соединенных между собой

с помощью логических операций. Символическое обозначение – F(A,B,…). Логические операции – логическое действие

Если составное высказывание (логическую функцию) выразить в виде формулы, в которую войдут логические переменные и знаки логических операций, то получится логическое выражение, значение которого можно вычислить.

Значением логического выражения могут быть только ИСТИНА (1) или ЛОЖЬ (0).

Составное высказывание – логическая функция, которая содержит несколько простых мыслей, соединенных между собой с помощью логических операций. Символическое обозначение – F(A,B,…).

Слайд 5А={Луна – планета}; В={2*2=4};
Простые высказывания
Любое высказывание либо истинно (1), либо ложно (0)

Слайд 6А={Луна – планета}; В={22=4}; А или В - Луна – планета или 22=4; А и В -

Луна – планета и 2*2=4; не А и не В - Луна не планета и 2*2не равно 4;

Составные высказывания

А={Луна – планета}; В={2*2=4}; А или В - Луна – планета или 2*2=4; А и В - Луна – планета

Слайд 7Таблицы истинности – таблицы, в которых по действиям показано, какие значения принимает логическое

выражение при всех возможных наборах его переменных

Причем, количество строк в таблице истинности вычисляется как 2n, где n – количество переменных, а
количество столбцов = количество переменных + количество логических операций.

Таблицы истинности – таблицы, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его

Слайд 8Конъюнкция (логическое умножение) – это логическая операция, ставящая в соответствие каждым двум простым

высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Конъюнкция (логическое умножение) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда

Слайд 9Дизъюнкция (логическое сложение) – это логическая операция, ставящая в соответствие каждым двум простым

высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, и истинным, когда хотя бы одно из двух образующих его высказываний истинно

Дизъюнкция (логическое сложение) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда

Слайд 10Инверсия (отрицание) – это логическая операция, которая каждому простому высказыванию ставит в соответствие

составное высказывание, заключающееся в том, что исходное высказывание отрицается.

Инверсия (отрицание) – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что

Слайд 11Импликация (логическое следование) – это логическая операция, ставящая в соответствие каждым двум простым

высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

Импликация (логическое следование) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда

Слайд 12При составлении логического выражения необходимо учитывать порядок выполнения логических операций:
Действия в

скобках;
Инверсия;
Конъюнкция;
Дизъюнкция (строгая и нестрогая);
Импликация;
Эквивалентность.

При составлении логического выражения необходимо учитывать порядок выполнения логических операций: Действия в скобках;Инверсия;Конъюнкция; Дизъюнкция (строгая и нестрогая);

Слайд 13В алгебре логики логические связки и соответствующие им логические операции имеют

специальные названия и обозначаются следующим образом:

Слайд 14Запись импликации с помощью инверсии, конъюнкции и дизъюнкции
Операцию «импликация» можно выразить

через «ИЛИ» и «НЕ»: A → B = ¬ A  B
или в других обозначениях

Запись импликации с помощью инверсии, конъюнкции и дизъюнкцииОперацию «импликация» можно выразить через «ИЛИ» и «НЕ»: A →

Слайд 15Иногда при решении задач полезны формулы де Моргана:
¬ (A  B)

= ¬ A  ¬ B ¬ (A  B) = ¬ A  ¬ B

Огастес (Август) де Морган – шотландский математик и логик.

Иногда при решении задач полезны формулы де Моргана:¬ (A  B) = ¬ A  ¬ B

Скачать презентацию

Презентация, доклад к уроку Основы логики

Содержание

Слайд 1Шабалдина Н. В.
Основы алгебры логики

Слайд 2Отцом алгебры логики по праву считается английский математик XIX столетия Джордж

Слайд 3Логическое высказывание – это повествовательное предложение, про которое однозначно можно сказать:

Слайд 4Составное высказывание – логическая функция, которая содержит несколько простых мыслей, соединенных между собой

Слайд 5А={Луна – планета}; В={2*2=4};
Простые высказывания
Любое высказывание либо истинно (1), либо ложно (0)

Слайд 6А={Луна – планета}; В={22=4}; А или В - Луна – планета или 22=4; А и В -

Слайд 7Таблицы истинности – таблицы, в которых по действиям показано, какие значения принимает логическое

Слайд 8Конъюнкция (логическое умножение) – это логическая операция, ставящая в соответствие каждым двум простым

Слайд 9Дизъюнкция (логическое сложение) – это логическая операция, ставящая в соответствие каждым двум простым

Слайд 10Инверсия (отрицание) – это логическая операция, которая каждому простому высказыванию ставит в соответствие

Слайд 11Импликация (логическое следование) – это логическая операция, ставящая в соответствие каждым двум простым

Слайд 12При составлении логического выражения необходимо учитывать порядок выполнения логических операций:
Действия в

Слайд 13В алгебре логики логические связки и соответствующие им логические операции имеют

Слайд 14Запись импликации с помощью инверсии, конъюнкции и дизъюнкции
Операцию «импликация» можно выразить

Слайд 15Иногда при решении задач полезны формулы де Моргана:
¬ (A  B)

Что такое shareslide.ru?

Обратная связь

Презентация, доклад к уроку Основы логики

Содержание

Слайд 1Шабалдина Н. В.Основы алгебры логики

Слайд 2Отцом алгебры логики по праву считается английский математик XIX столетия Джордж

Слайд 3Логическое высказывание – это повествовательное предложение, про которое однозначно можно сказать:

Слайд 4Составное высказывание – логическая функция, которая содержит несколько простых мыслей, соединенных между собой

Слайд 5А={Луна – планета}; В={2*2=4}; Простые высказыванияЛюбое высказывание либо истинно (1), либо ложно (0)

Слайд 6А={Луна – планета}; В={2*2=4}; А или В - Луна – планета или 2*2=4; А и В -

Слайд 7Таблицы истинности – таблицы, в которых по действиям показано, какие значения принимает логическое

Слайд 8Конъюнкция (логическое умножение) – это логическая операция, ставящая в соответствие каждым двум простым

Слайд 9Дизъюнкция (логическое сложение) – это логическая операция, ставящая в соответствие каждым двум простым

Слайд 10Инверсия (отрицание) – это логическая операция, которая каждому простому высказыванию ставит в соответствие

Слайд 11Импликация (логическое следование) – это логическая операция, ставящая в соответствие каждым двум простым

Слайд 12При составлении логического выражения необходимо учитывать порядок выполнения логических операций: Действия в

Слайд 13В алгебре логики логические связки и соответствующие им логические операции имеют

Слайд 14Запись импликации с помощью инверсии, конъюнкции и дизъюнкцииОперацию «импликация» можно выразить

Слайд 15Иногда при решении задач полезны формулы де Моргана:¬ (A  B)

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1Шабалдина Н. В.
Основы алгебры логики

Слайд 5А={Луна – планета}; В={2*2=4};
Простые высказывания
Любое высказывание либо истинно (1), либо ложно (0)

Слайд 6А={Луна – планета}; В={22=4}; А или В - Луна – планета или 22=4; А и В -

Слайд 12При составлении логического выражения необходимо учитывать порядок выполнения логических операций:
Действия в

Слайд 14Запись импликации с помощью инверсии, конъюнкции и дизъюнкции
Операцию «импликация» можно выразить

Слайд 15Иногда при решении задач полезны формулы де Моргана:
¬ (A  B)