- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Логические операции
Содержание
- 1. Логические операции
- 2. Конъюнкция Составное высказывание, образованное в результате конъюнкции
- 3. ДизъюнкцияСоставное высказывание, образованное в результате дизъюнкции ложно
- 4. ИнверсияТаблица истинностиСоответствует частице «не» обозначается _ или
- 5. Операция «Исключающее ИЛИ»Обозначается х1⊕x2 или х1 XOR х2
- 6. В таблице приведены запросы к поисковому
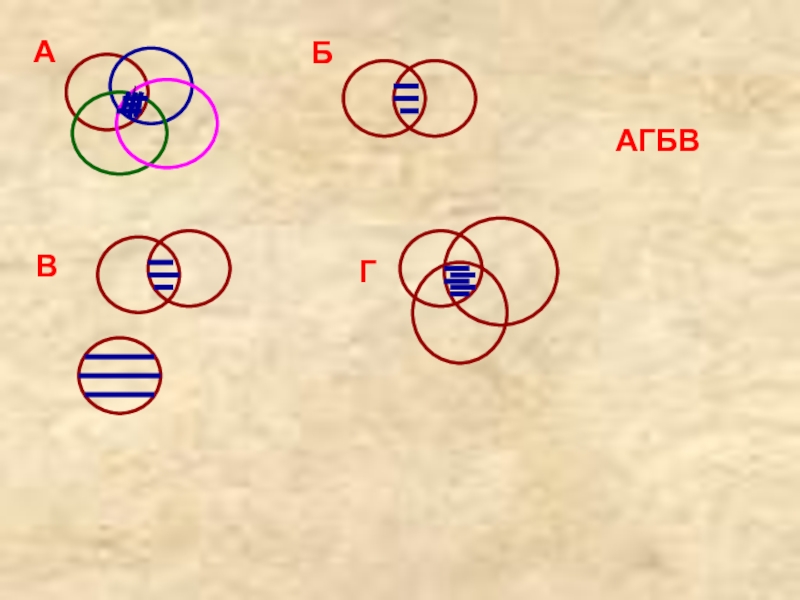
- 7. АГБВ АБВГ
- 8. В таблице приведены запросы к поисковому серверу.Расположите
- 9. логические выражения
- 10. Каждое составное высказывание можно выразить в виде
- 11. 2. Определить при каких значениях числа Х
- 12. Построение таблиц истинности логического выражения:
- 13. Не (0 V 0) Λ (не 0
- 14. Логические выражения, значения которых в таблицахистинности совпадают,
- 15. логические функции
- 16. Логические выражения можно рассматривать как логическую функцию
- 17. Импликация Составное высказывание, образованное в результате импликации
- 18. Пример1. Высказывание «Если число делится на 10,
- 19. Функции a → b и выражение ¬
- 20. Эквивалентность Составное высказывание, образованное в результатеэквивалентности истинно
- 21. Пример1. Высказывание «Компьютер может работать тогда и
- 22. Функции a ~ b и выражения (¬
- 23. 1. Построить таблицу истинности логического выражения.a &
Слайд 2Конъюнкция
Составное высказывание, образованное в результате
конъюнкции истинно тогда и только
когда истинны все входящие в него простые высказывания.
Таблица истинности
Соответствует союзу «и»
обозначается & или *, или Λ;
в языках программирования обозначается and,
иначе называется логическим умножением.
0
0
0
1
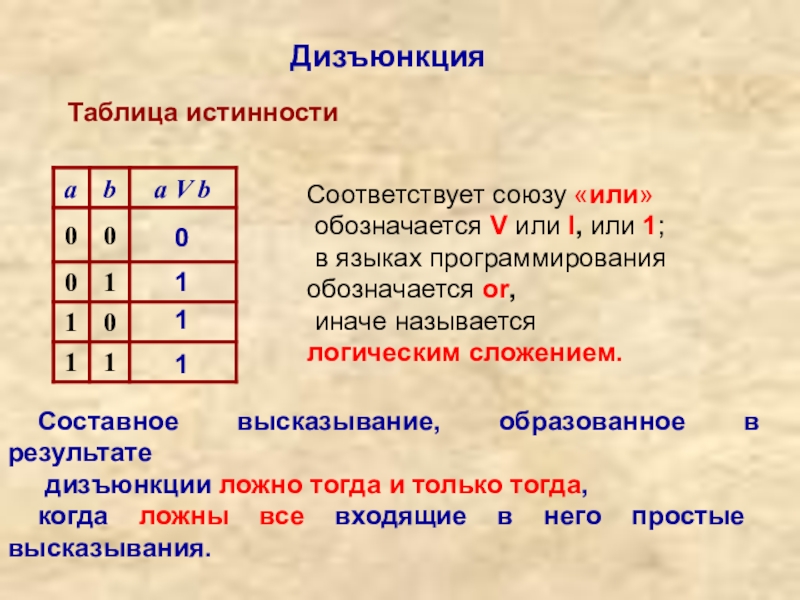
Слайд 3Дизъюнкция
Составное высказывание, образованное в результате
дизъюнкции ложно тогда и только тогда,
когда ложны все входящие в него простые высказывания.
Таблица истинности
Соответствует союзу «или»
обозначается V или I, или 1;
в языках программирования обозначается or,
иначе называется логическим сложением.
0
1
1
1
Слайд 4Инверсия
Таблица истинности
Соответствует частице «не»
обозначается _ или ¬;
в языках программирования
иначе называется логическим сложением.
1
0
Инверсия делает истинное высказывание
ложным и, наоборот, ложное – истинным.
Слайд 6 В таблице приведены запросы к поисковому серверу.
Расположите обозначения запросов
количества страниц, которые найдет поисковый сервер по
каждому запросу.
Для обозначения логической операции “ИЛИ” в запросе
используется символ |,
а для логической операции “И” – символ &.
Слайд 8В таблице приведены запросы к поисковому серверу.
Расположите обозначения запросов в порядке
количества страниц, которые найдет поисковый сервер
по каждому запросу.
ГВАБ
Слайд 10Каждое составное высказывание можно
выразить в виде формулы (логического выражения),
в которую
логических операций.
Приоритет логических операций:
инверсия
конъюнкция
дизъюнкция
Слайд 112. Определить при каких значениях числа Х предикат первого порядка примет
а) ложь;
б) истина.
а) (x>8) или (x<-3)
б) -3<= x<=8
Слайд 12Построение таблиц истинности логического
выражения:
1. Определить n
входящих в выражение.
2. Вычислить q - количество строк в таблице
по формуле: 2n.
3. Внести в таблицу возможные наборы
значений исходных переменных.
Например.
Построить таблицу истинности для логического выражения: ¬(a V b) Λ (¬a V b).
Решение: n = 2, q = 4.
Слайд 13Не (0 V 0) Λ (не 0 V 0) = не
Не (0 V 1) Λ (не 0 V 1) = не 1 Λ (1 V 1)=0 Λ 1 = 0;
Не (1 V 0) Λ (не 1 V 0) = не 1 Λ (0 V 0)=0 Λ 0 = 0;
Не (1 V 1) Λ (не 1 V 1) = не 1 Λ (0 V 1)=0 Λ 1 = 0;
1
0
0
0
Слайд 14Логические выражения, значения которых в таблицах
истинности совпадают, называются равносильными.
Обозначается «=»
Пример.
¬
Логические выражения, у которых значения в таблицах истинности состоят из 0, называются
тождественно ложными.
Например. ¬ a & а
Логические выражения, у которых значения в таблицах истинности состоят из 1, называются
тождественно истинными.
Например. ¬ a или а
Слайд 16Логические выражения можно рассматривать как
логическую функцию F(x1, x2, …xn).
Функция
Логическая функция от 2-х аргументов
имеет 4 возможных значения.
Каждое значение – 1 бит информации, значит каждая
Функция несет 4 бита информации.
По формуле N=2i, N=24=16.
Существует 16 логических функций
от двух аргументов.
Слайд 17Импликация
Составное высказывание, образованное в результате
импликации ложно тогда и только
когда из истинной посылки следует ложный вывод.
Таблица истинности
Соответствует обороту речи «если…, то…»
обозначается →
называется логическим следованием.
1
1
0
1
Слайд 18
Пример1. Высказывание «Если число делится на 10, то оно делится на
Пример2. Высказывание «Если число делится на 10, то оно делится на 3» ложно т.к. истинна посылка, но ложен вывод.
Слайд 20Эквивалентность
Составное высказывание, образованное в результате
эквивалентности истинно тогда и только тогда,
когда оба высказывания одновременно либо истинны,
либо ложны.
Таблица истинности
Соответствует обороту речи «тогда и только тогда, когда…»
обозначается ~
называется логическим равенством.
1
0
0
1
Слайд 21
Пример1. Высказывание «Компьютер может работать тогда и только тогда, когда он
Пример2. Высказывание «Компьютер не может работать тогда и только тогда, когда он не включен» истинно.
Пример3. Высказывание «Компьютер может работать тогда и только тогда, когда он не включен» ложно.
Слайд 22
Функции a ~ b и выражения
(¬ a или b)& (a
(¬ a & ¬ b)V (a & b) равносильны.
Доказательство.
1
0
0
1
Вывод: a ~ b = (¬ a или b)& (a или ¬ b)
Слайд 231. Построить таблицу истинности логического выражения.
a & (b V ¬ b
2. Доказать равносильность выражений.
и a & (b V ¬ b & ¬ c)
(a V b) & (¬ a V ¬ b)