- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок Решение задач на растворы и сплавы
Содержание
- 1. Урок Решение задач на растворы и сплавы
- 2. Цель урока Рассмотрение алгоритма
- 3. Задачи урока:Совершенствовать умения и навыки решения задач
- 4. Только из союза двух работающих вместе и
- 5. Слайд 5
- 6. 2) Выразите в виде десятичной дроби:17%, 40%,
- 7. Устный счет3) Выразите в виде обыкновенной дроби
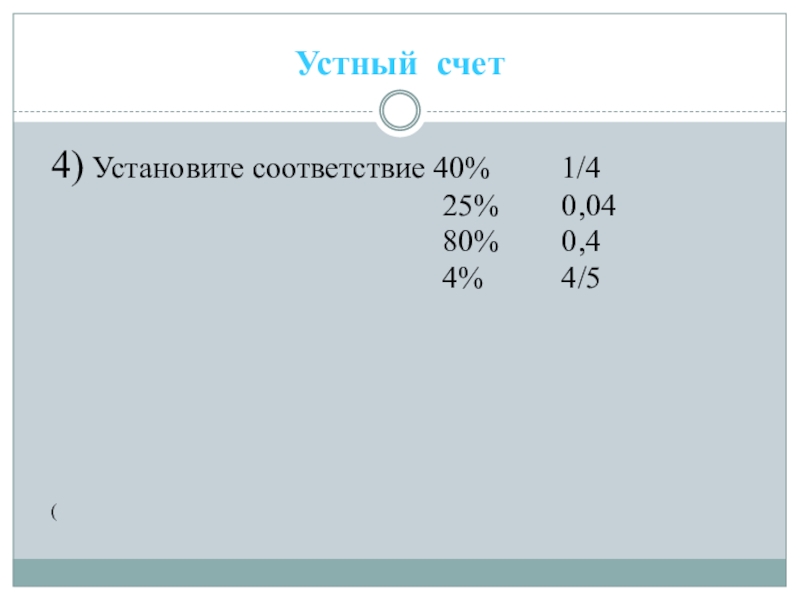
- 8. Устный счет4) Установите соответствие 40% 1/4 25% 0,04 80% 0,4 4% 4/5(
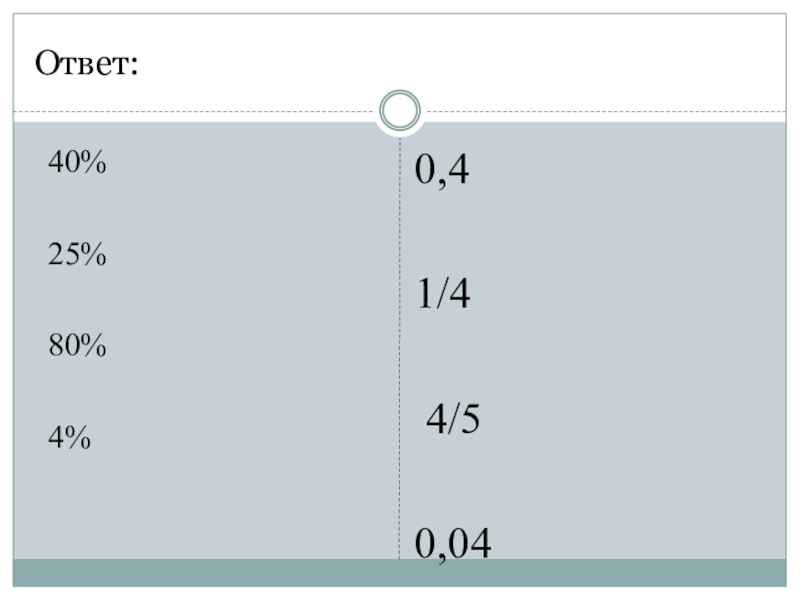
- 9. Ответ:40% 25% 80% 4% 0,41/4 4/50,04
- 10. Устный счет5) Одним из основных действий
- 11. Ответ:1) % записать в виде дроби,2) умножить число на эту дробь.
- 12. Устный счет6) Найти 10% от 30.
- 13. Устный счет7) Вычислите :
- 14. Устный счетОтвет: а) Найти 20% от
- 15. Смеси -
- 16. Знаете ли вы, что… В каждой
- 17. Для засолки грибов необходимо приготовить 12
- 18. Знаете ли вы, что…Витаминный, ягодный или фруктовый
- 19. ¾ поверхности Земли покрыто водой
- 20. Человек на 70% состоит из воды
- 21. В сутки человек выделяет 3 литра воды и столько же нужно ввести в организм
- 22. Овощи содержат 90% воды (рекордсмены – огурцы - 98%)
- 23. Рыба содержит 80% воды (рекордсмен у животных – медуза 98%)
- 24. Хлеб – 40%
- 25. Молоко – 75%
- 26. «ДОЛЯ»Объемная доля газообразного компонента А в системе
- 27. Задача №1 Перед посадкой семена томатов дезинфицируют
- 28. Задача №2 При смешивании 10%-го и 30%-го
- 29. Решение:
- 30. Решение Кол. Раствора
- 31. Задача № 2 Решение: m1 = (14
- 32. При решении задач на растворы с разными
- 33. Задача №3. Один раствор содержит 55% азотной
- 34. кол
- 35. Задача 4 Из сосуда, доверху наполненного 97%
- 36. 1раствор - х, %
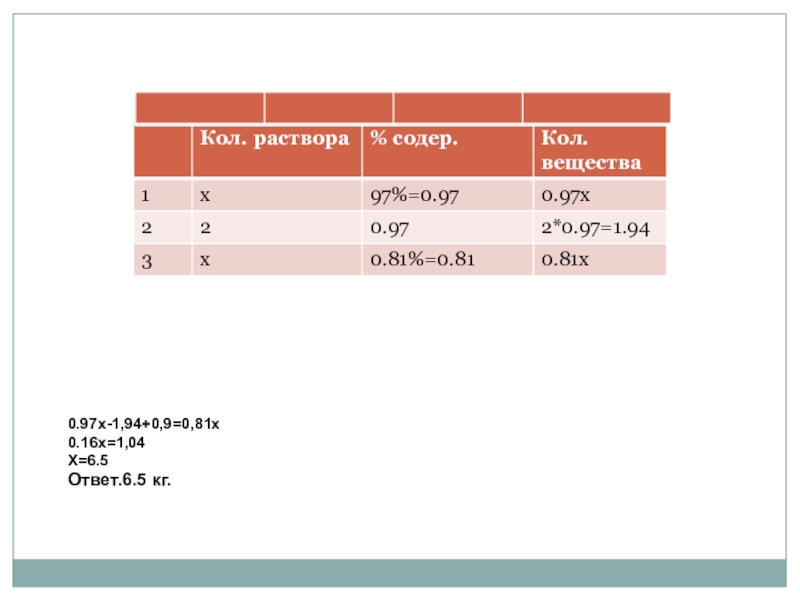
- 37. 0.97х-1,94+0,9=0,81х0.16х=1,04Х=6.5Ответ.6.5 кг.
- 38. Задача 5. Сплавили 300 г сплава олова
- 39. 1200*0,01х=9000,01х=900:1200Х=0,75:0.01Х=75Ответ:75%
- 40. Задача 1. Смешали некоторое количество 15-процентного
- 41. Проверочная работа 1 вариант
- 42. Решения задач проверочной работы 1 вариант
- 43. Критерий оценивания (самопроверка)нет ошибок – «5» одна ошибка – «4»две ошибки – «3»
- 44. Домашнее задание Задача №1 Какую
- 45. Задание на дом.1.Имеются два сосуда, содержащие 42кг
- 46. Рефлексия. Оцените усвоение материала (самооценка):Устный счет
- 47. Смайлики
- 48. СПАСИБО ЗА УРОК
Слайд 1Решение задач на растворы и сплавы
Интегрированный урок химии и математики
Учитель математики
МОУ лицей №2Блесткина Л.П.
Учитель химии высшей категории
МОУ лицей №2 Суслова Е.Т.
Слайд 2Цель урока
Рассмотрение алгоритма решения задач на растворы:
Слайд 3Задачи урока:
Совершенствовать умения и навыки решения задач на растворы по алгоритмам;
развивать
развивать практические умения работы с химической посудой и веществами;
сформировать целостную картину о взаимосвязи предметов в школе;
рассмотреть биологическое значение воды, как универсального растворителя;
учить учащихся самооценке, самоконтролю.
Слайд 4
Только из союза двух работающих вместе и при помощи друг друга
Антуан де Сент- Экзюпери
Слайд 62) Выразите в виде десятичной дроби:
17%,
40%,
6%.
Ответ:
17% = 0,17
40%
6% = 0,06
Устный счет
Слайд 10Устный счет
5) Одним из основных действий
с процентами – нахождение %
Как найти % от числа?
Слайд 12Устный счет
6) Найти 10% от 30.
Ответ:
1) % записать
10% = 0,1
2) умножить число на эту дробь
30 * 0,1 = 3
Слайд 14Устный счет
Ответ:
а) Найти 20% от 70.
б) Найти 6% от 20.
6% = 0,06 и 20 * 0,06 = 1,2
в) Найти х% от 7.
х% = х / 100 и х / 100 * 7
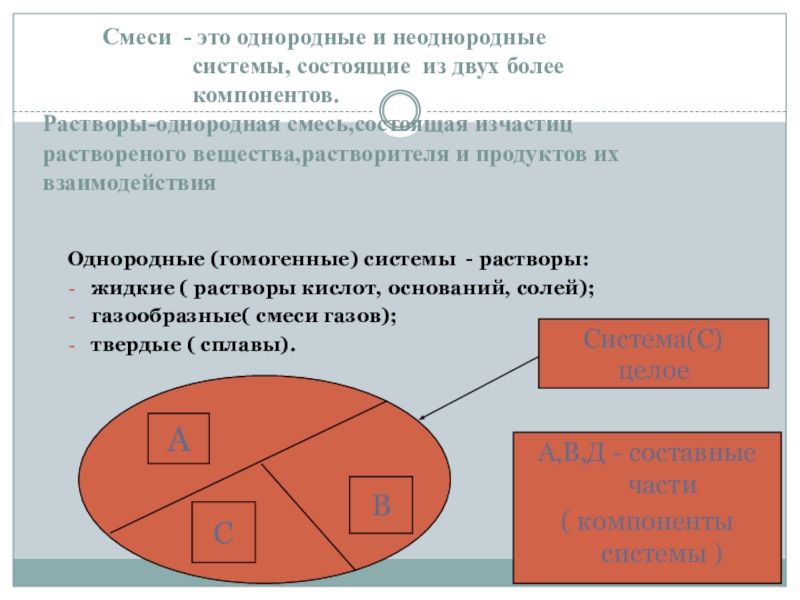
Слайд 15 Смеси - это однородные и неоднородные
Однородные (гомогенные) системы - растворы:
жидкие ( растворы кислот, оснований, солей);
газообразные( смеси газов);
твердые ( сплавы).
А
Система(С) целое
А,В,Д - составные части
( компоненты системы )
В
С
Слайд 16Знаете ли вы, что…
В каждой домашней аптечке есть:
10% -
5% - ный спиртовой раствор йода,
1% - ный спиртовой раствор бриллиантового зеленого,
3% - ный спиртовой раствор борной кислоты
Слайд 17Для засолки грибов необходимо приготовить
12 %-ный солевой раствор.
А
Слайд 18Знаете ли вы, что…
Витаминный, ягодный или фруктовый компот особенно хорош зимой.
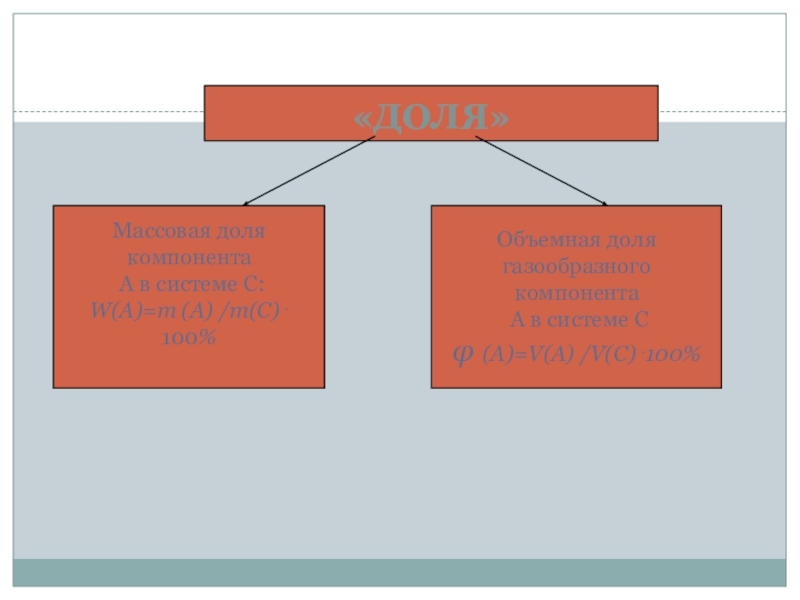
Слайд 26«ДОЛЯ»
Объемная доля
газообразного компонента
А в системе С
φ (A)=V(A) /V(C) .100%
Массовая
компонента
А в системе С:
W(A)=m (A) /m(C) . 100%
Слайд 27Задача №1
Перед посадкой семена томатов дезинфицируют 15%-ным раствором марганцовки.
Сколько
Слайд 28Задача №2
При смешивании 10%-го и 30%-го раствора марганцовки получают 200
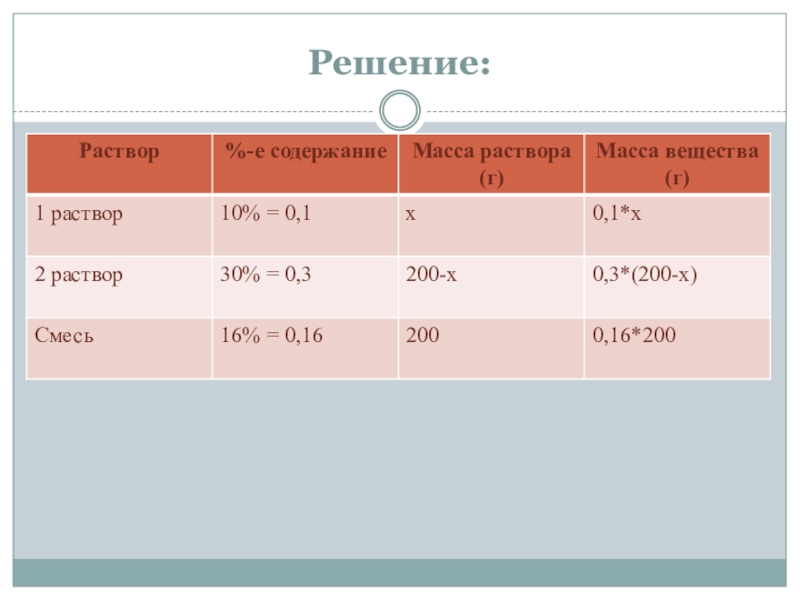
Слайд 30Решение
Кол. Раствора % содерж.
1 х 10 % 0,1х
2 200-х 30% 0,3(200-х)
3 200 16% 0,16*200
Составим уравнение: 0,1х+0,3(200-х)=0,16*200
-0,2х+60=32
-0,2х=-28
Х=140
200-140=60.
Ответ.140г и 60г.
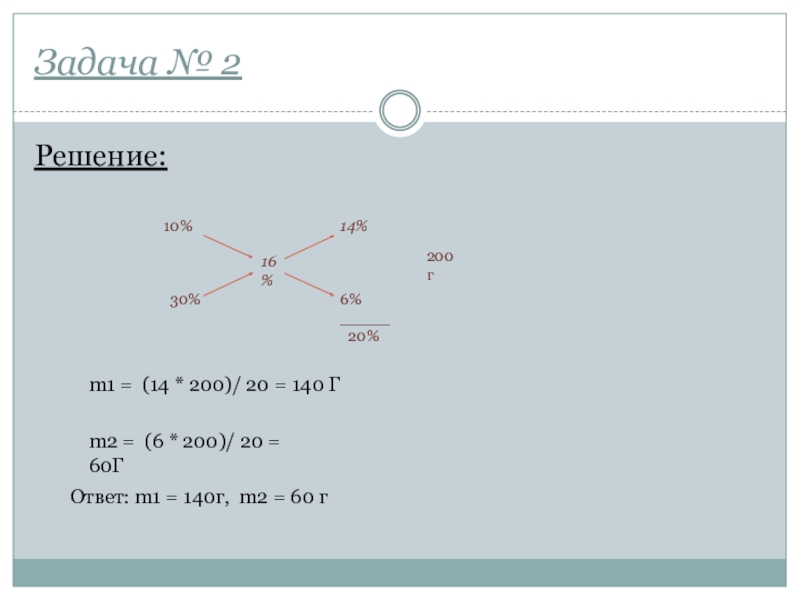
Слайд 31Задача № 2
Решение:
m1 = (14 * 200)/ 20 =
m2 = (6 * 200)/ 20 = 60Г
Ответ: m1 = 140г, m2 = 60 г
Слайд 32
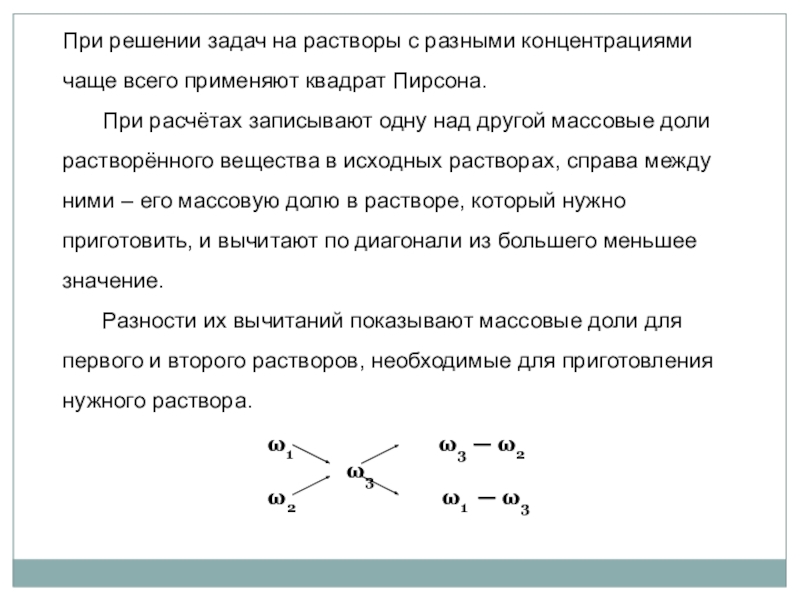
При решении задач на растворы с разными концентрациями чаще всего применяют
При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение.
Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
Слайд 33Задача №3. Один раствор содержит 55% азотной кислоты, а второй 30%.
Слайд 34 кол раств
1 х 55% 0,55х
2 100-х 30% 0,3(100-х)
3 100 50% 0,5*100
0,55х+0,3(100-х)=0,5*100
0,25х=50-30
0,25х=20
Х=80.
Ответ. 80кг и 20кг.
Слайд 35Задача 4
Из сосуда, доверху наполненного 97% раствором кислоты, отлили 2
Решение:
97%
81%
45%
Слайд 361раствор - х, % содержание -97, следовательно вещества
Составим уравнение: 0,97х-1,94+0.9=0,81х
0,16х=1,04
Х=6,5
Слайд 38Задача 5. Сплавили 300 г сплава олова и меди, содержащего 60%
Решение:
Слайд 40Задача 1. Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же
ра этого вещества. Сколько процентов составляет концентрация
получившегося раствора? Ответ: 17%.
Задача 2.
Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Ответ: 21%.
Задача 3. Имеется два сплава. Первый содержит 10% никеля,
второй — 30% никеля. Из этих двух сплавов получили третий
сплав массой 200 кг, содержащий 25% никеля. На сколько
килограммов масса первого сплава меньше массы второго?
Ответ: на 100 кг.
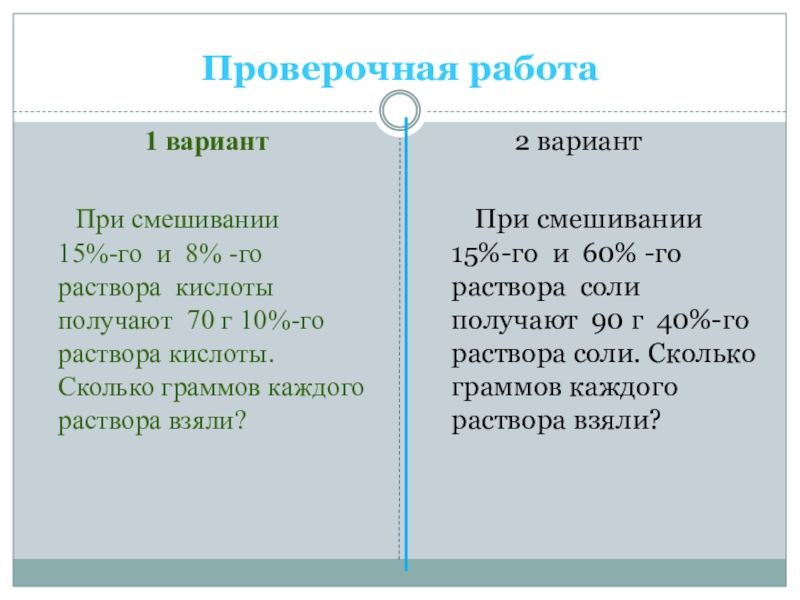
Слайд 41Проверочная работа
1 вариант
При
2 вариант
При смешивании
15%-го и 60% -го раствора соли получают 90 г 40%-го раствора соли. Сколько граммов каждого раствора взяли?
Слайд 42Решения задач проверочной работы
1 вариант
0,15х
0,15х+ 5,6-0,08х =7
0,07х=7-5,6
0,07х=1,4
х = 1,4:0,07
х = 20
20(г) - 15% раствора.
70 – 20 = 50(г)-8% раствора
Ответ: 20 г, 50г.
2 вариант
0,15х+0,6(90-х)=0,4*90
0,15х+54-0,6х=36
-0,45х=36-54
-0,45х =-18
х = 18:0,45
х = 40
40(г) -15% раствора
90 – 40 = 50(г)-60% раствора
Ответ: 40 г, 50г.
Слайд 44Домашнее задание
Задача №1
Какую массу молока 10%-й жирности и
Задача №2
Для засола огурцов используют 7% водный раствор поваренной соли (хлорида натрия NaCl). Именно такой раствор в достаточной мере подавляет жизнедеятельность болезнетворных микроорганизмов и плесневого грибка, и в то же время не препятствует процессам молочнокислого брожения. Рассчитайте массу соли и массу воды для приготовления 1 кг такого раствора?
Слайд 45Задание на дом.
1.Имеются два сосуда, содержащие 42кг и 6кг раствора кислоты
2. Смешали 14 литров 30% водного раствора некоторого вещества с 10 литрами 18-процентного раствора этого же вещества. Сколько % составляет концентрация получившегося раствора?
3.Смешав 70% и 60% растворы кислоты и добавив 2кг чистой воды, получили 50% раствор кислоты. Если бы вместо2кг воды добавили 2кг 90% раствора той же кислоты, то получили бы70% раствор кислоты. Сколько кг 70% раствора использовали для получения смеси?
Слайд 46Рефлексия.
Оцените усвоение материала (самооценка):
Устный счет на проценты (математика)
Устная работа (химия)
Решение
Решение задачи №2 (математика И ХИМИЯ)
Решение задачи №3 (математика И ХИМИЯ)
Решение задачи №4 (математика И ХИМИЯ)
Отметка за проверочную работу (самооценка)