- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по химии на тему Решение задач на растворы (9 класс)
Содержание
- 1. Презентация по химии на тему Решение задач на растворы (9 класс)
- 2. Слайд 2
- 3. Основными компонентами в задачах на растворы являются:
- 4. Задача 1. Смешав 40%-ный
- 5. Получаем уравнение: 0,4x + 0,15y + 0,8
- 6. {{0,4x + 0,15y = 0,2x + 0,2y
- 7. {
- 8. {0,4x + 0,15y = 0,2(x + y
- 9. Задача 2. Сколько нужно
- 10. Слайд 10
- 11. Решите уравнения и получите название однородной системы,
- 12. Задача 3. Лимонная кислота содержится не только
- 13. Задача 4. Свежий гриб содержит 90% воды,
- 14. Математика - это язык, на котором говорят
Слайд 1РЕШЕНИЕ ЗАДАЧ
НА РАСТВОРЫ
Учитель химии МОУ СОШ №32
Учитель математики МОУ СОШ №32
Зольникова М.И.
Слайд 3
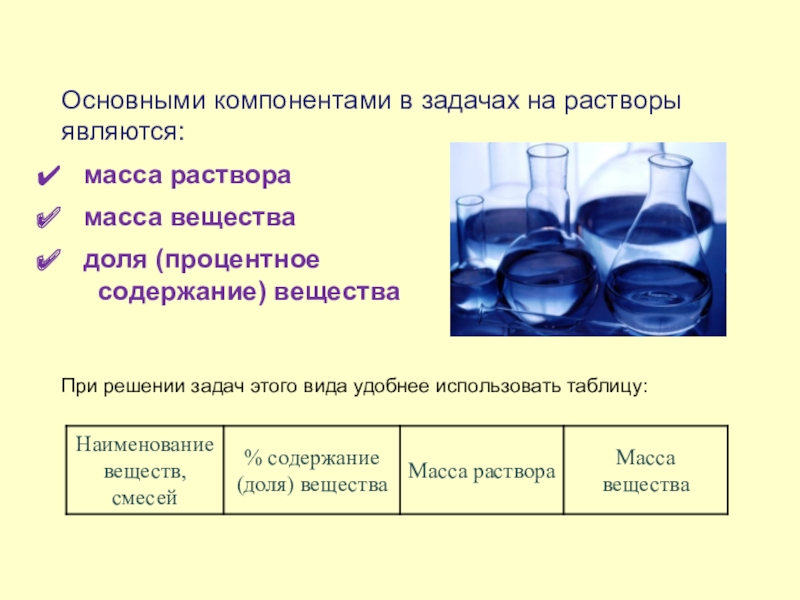
Основными компонентами в задачах на растворы являются:
масса раствора
доля (процентное
содержание) вещества
При решении задач этого вида удобнее использовать таблицу:
Слайд 4 Задача 1. Смешав 40%-ный и 15%-ный растворы кислоты и добавив 3кг
Получаем уравнение:
0,4x + 0,15y = 0,2(x + y + 3)
Слайд 5Получаем уравнение:
0,4x + 0,15y + 0,8 · 3 = 0,5(x
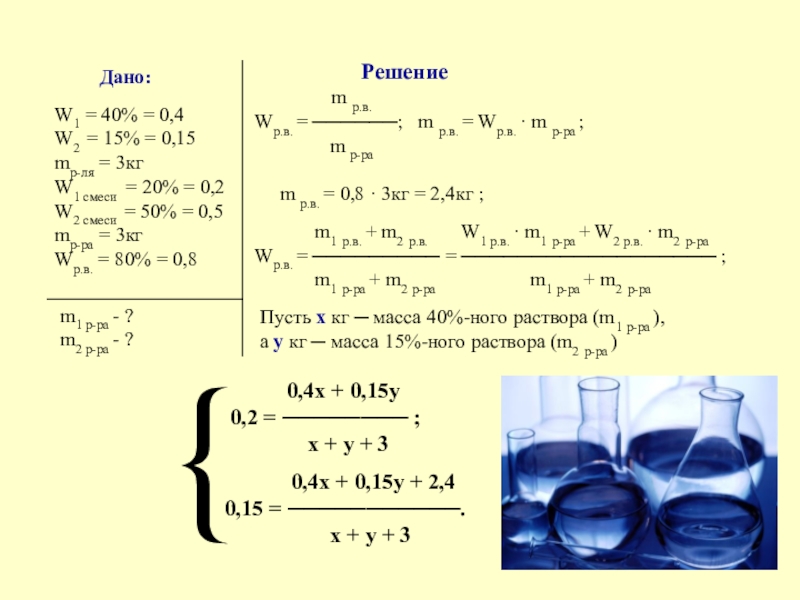
Задача 1. Смешав 40%-ный и 15%-ный растворы кислоты и добавив 3кг чистой воды получили 20%-ный раствор кислоты. Если бы вместо 3кг воды добавили 3кг 80%-ного раствора той же кислоты, то получили бы 50%-ный раствор кислоты. Сколько килограммов 40%-ного и 15%-ного растворов кислоты было смешано?
Слайд 6{
{
0,4x + 0,15y = 0,2x + 0,2y + 0,6;
0,4x + 0,15y
{
0,2x - 0,05y = 0,6;
-0,1x - 0,35y = - 0,9.
|
X 2
{
0,2x - 0,05y = 0,6;
-0,2x - 0,7y = - 1,8.
-0,75y = - 1,2
y = 1,6
0,2 x- 0,05 ∙1,6 = 0,6
0,2x - 0,08 = 0,6
0,2x = 0,68
x = 3,4 Ответ: Было смешано 3,4 кг 40%-ного и
1,6 кг 15%-ного растворов кислоты.
0,4x + 0,15y = 0,2(x + y + 3);
0,4x + 0,15y + 0,8 ·3 = 0,5(x + y + 3).
Для решения задачи получаем систему уравнений:
Слайд 8{
0,4x + 0,15y = 0,2(x + y + 3);
0,4x + 0,15y
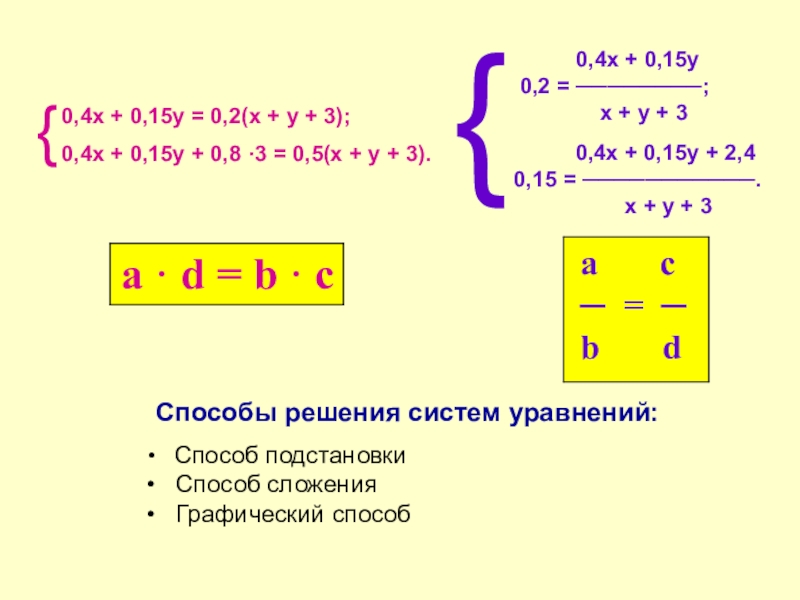
0,4х + 0,15у
0,2 = ────────;
х + у + 3
0,4х + 0,15у + 2,4
0,15 = ───────────.
х + у + 3
{
Способы решения систем уравнений:
Способ подстановки
Способ сложения
Графический способ
Слайд 9 Задача 2. Сколько нужно добавить воды в сосуд, содержащий
Анализируя таблицу, составим и решим уравнение:
0,08(200 + x) = 0,7 · 200
16 + 0,08х = 140
0,08х = 124
х = 1550 Ответ: Нужно добавить
1550г воды.
Слайд 10
m р.в.
Wр.в. = ──────; m р.в. = Wр.в. · m р-ра ;
m р-ра
m р.в. = 0,7 · 200г = 140г ;
Пусть x г ─ масса растворителя (mр-ля ), тогда:
140.
0,08. = ───── ;
200 + х
0,08(200 + х) = 140
16 + 0,08х = 140
0,08х = 124
х = 1550
Ответ: Нужно добавить 1550г воды.
Слайд 11Решите уравнения и получите название однородной системы, состоящей из частиц растворенного
Р А С Т В О Р
Слайд 12Задача 3. Лимонная кислота содержится не только в лимонах, но также
Определите, какая масса 10%-ного и 70%-ного раствора лимонной кислоты потребуется для приготовления 100г 18%-ного раствора?
Слайд 13Задача 4. Свежий гриб содержит 90% воды, а сушеный 15%. Сколько
получится сушеных грибов из 17 кг свежих?
(практически любой продукт - яблоки, грибы, картофель, крупа, хлеб и т.д. состоит из воды и сухого вещества. Причем воду содержат как свежие, так и сушеные продукты. Обратите внимание на то, что в процессе высыхания испаряется только вода, а сухое вещество никуда не девается и его масса не изменяется).
Слайд 14Математика - это язык, на котором говорят все точные науки.
Н.И. Лобачевский
Разве ты не заметил, что способный к математике изощрен во всех науках в природе?
Платон
Стремящийся к ближайшему изучению химии должен быть сведущ и
в математике.
М.В. Ломоносов
В каждой естественной науке заключено столько истины, сколько
в ней есть математики.
И. Кант
Если мы действительно что-то знаем, то мы знаем это благодаря изучению математики.
Пьер Гассенди
Подобно тому как все искусства тяготеют к музыке, все науки стремятся к математике.
Джордж Сантаяна
Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.
А.Н. Крылов