Разработано учителем математики
МОУ «СОШ» п. Аджером
Корткеросского района Республики Коми
Мишариной Альбиной Геннадьевной
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Задачи на тела вращения
Содержание
- 1. Задачи на тела вращения
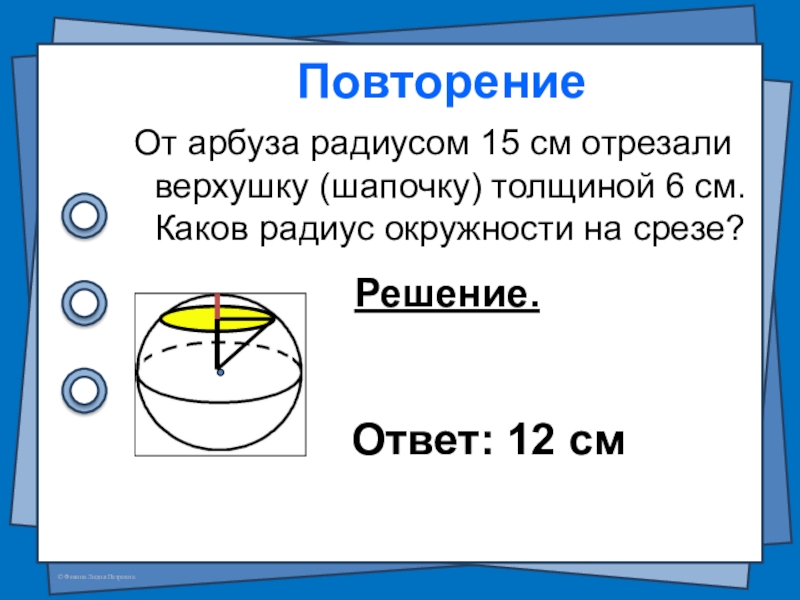
- 2. Повторение От арбуза радиусом 15 см отрезали
- 3. Содержание123456712111098141321201918171615272625242322Дополнительные1234
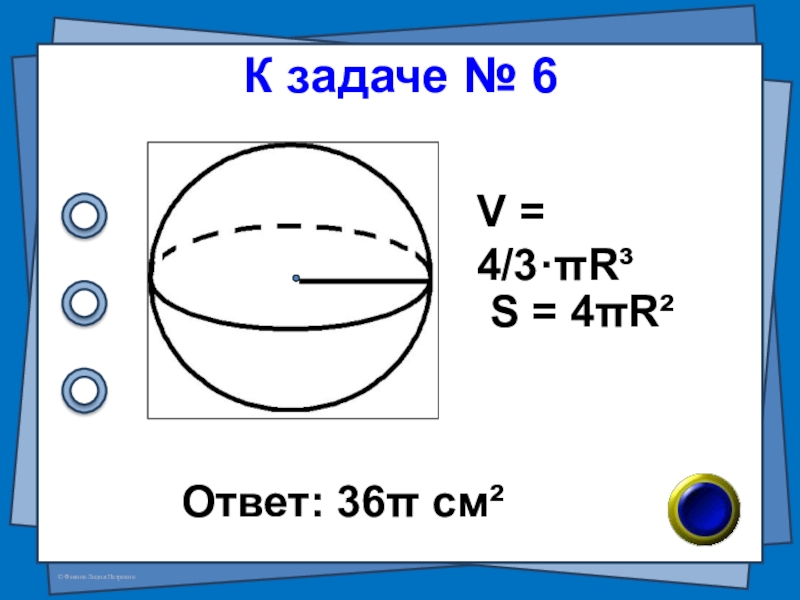
- 4. В-25 №7 Объём шара равен 36π см³. Найдите площадь поверхности шара. № 6
- 5. К задаче № 6Ответ: 36π см²S = 4πR²V = 4/3·πR³
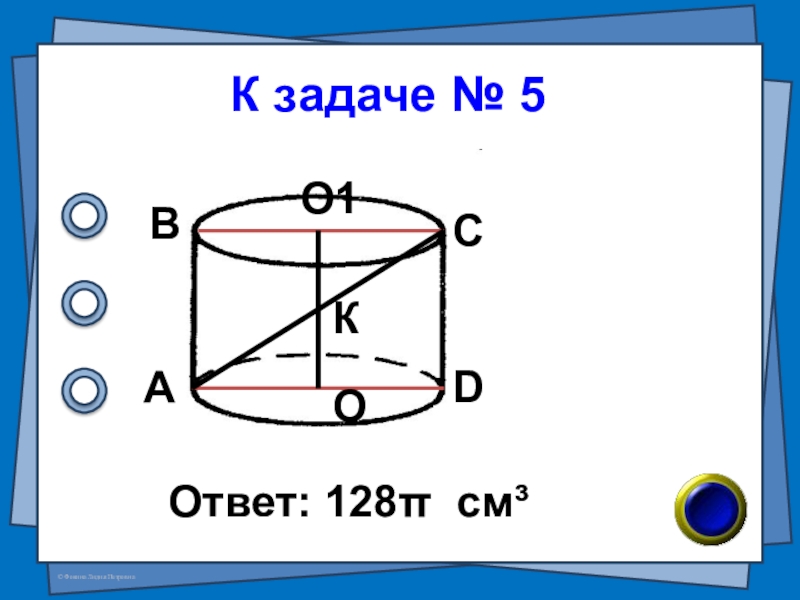
- 6. № 5 (В-18 №7) Осевым сечением
- 7. К задаче № 5Ответ: 128π см³АВСDОО1К
- 8. №4 (В-13 №7)Найдите объём тела,
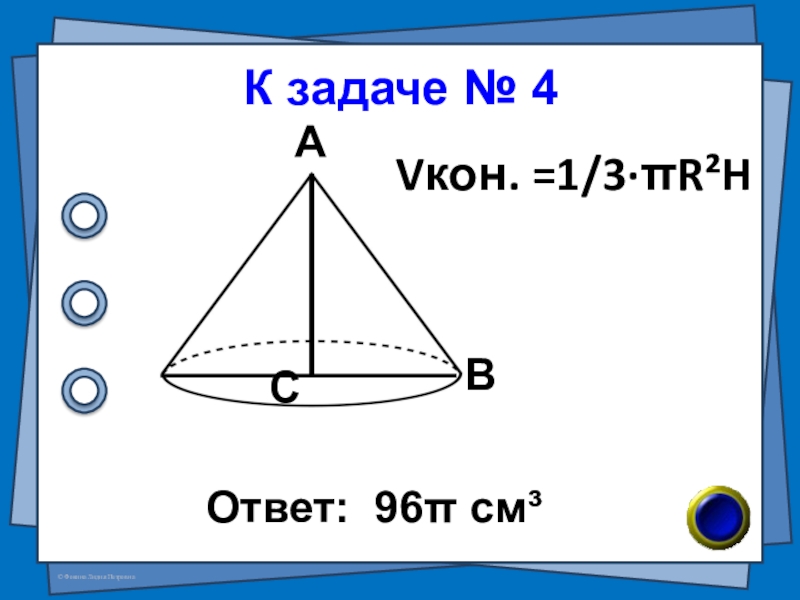
- 9. К задаче № 4
- 10. № 3 (В-9 №7)Найдите объём тела,
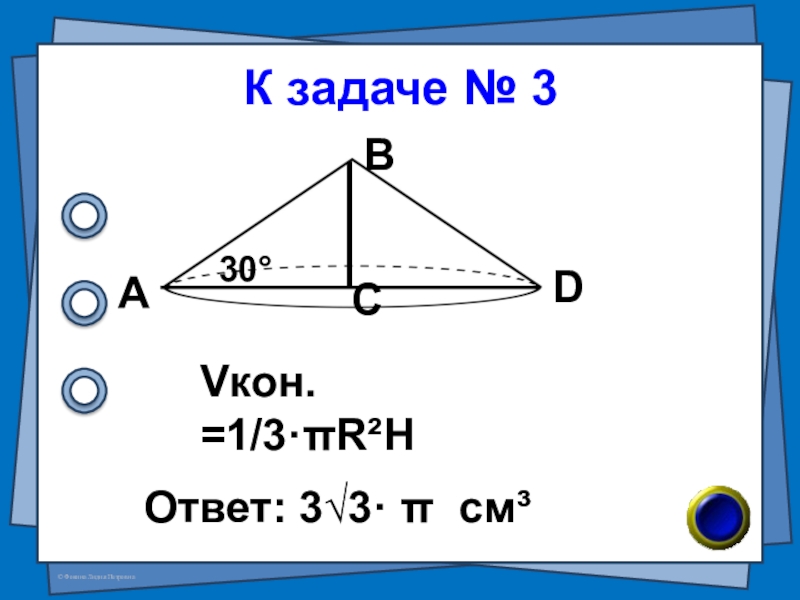
- 11. К задаче № 3Ответ: 3√3· π см³АВСD30°Vкон. =1/3·πR²H
- 12. № 2 (В-4 №7) Радиус основания
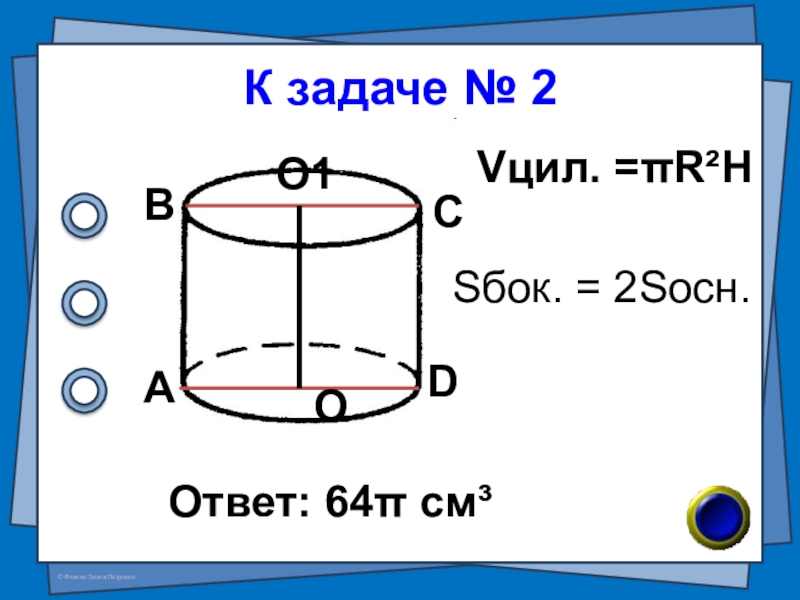
- 13. К задаче № 2Ответ: 64π см³АВСDОО1Vцил. =πR²HSбок. = 2Sосн.
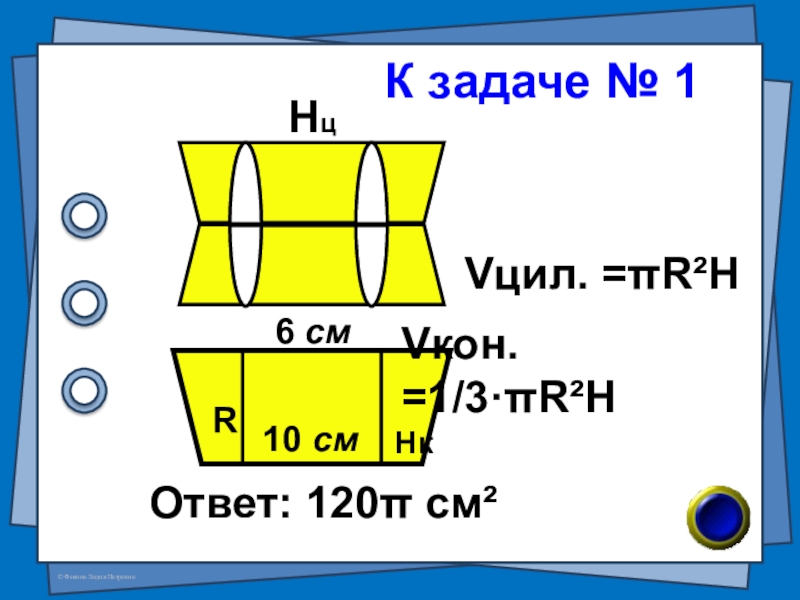
- 14. № 1 Равнобедренная трапеция, основания которой равны
- 15. Слайд 15
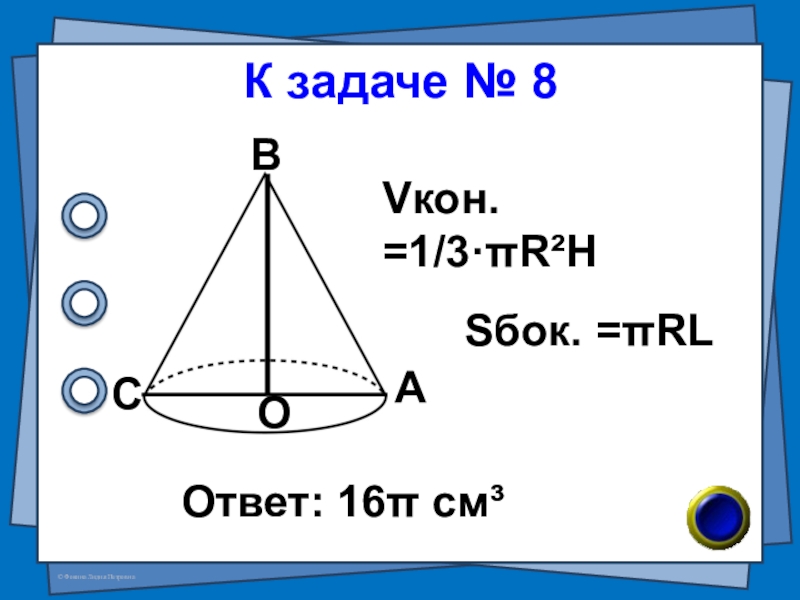
- 16. № 8 (В-31 №7)Площадь боковой поверхности конуса
- 17. К задаче № 8Ответ: 16π см³АВСОVкон. =1/3·πR²HSбок. =πRL
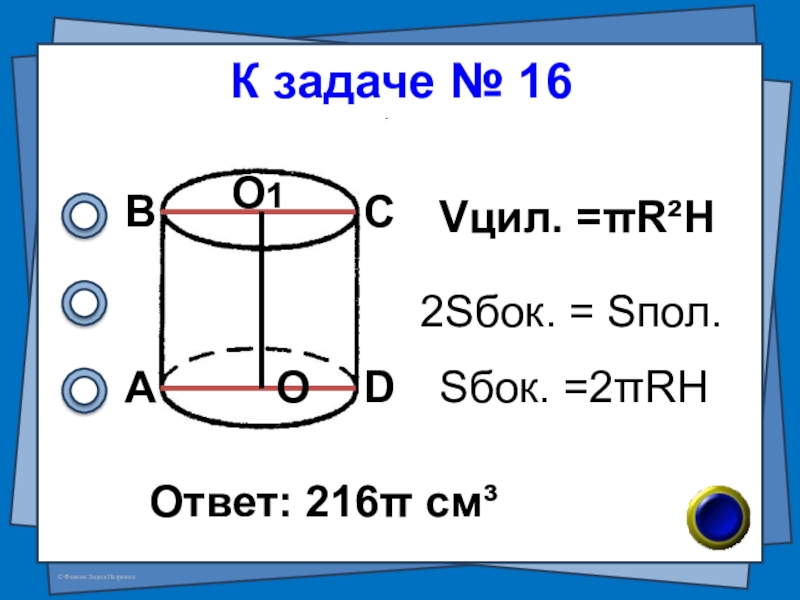
- 18. № 16 (В-63 №7)Высота цилиндра равна 6см,
- 19. К задаче № 16Ответ: 216π см³АВСDОО1Vцил. =πR²H2Sбок. = Sпол.Sбок. =2πRH
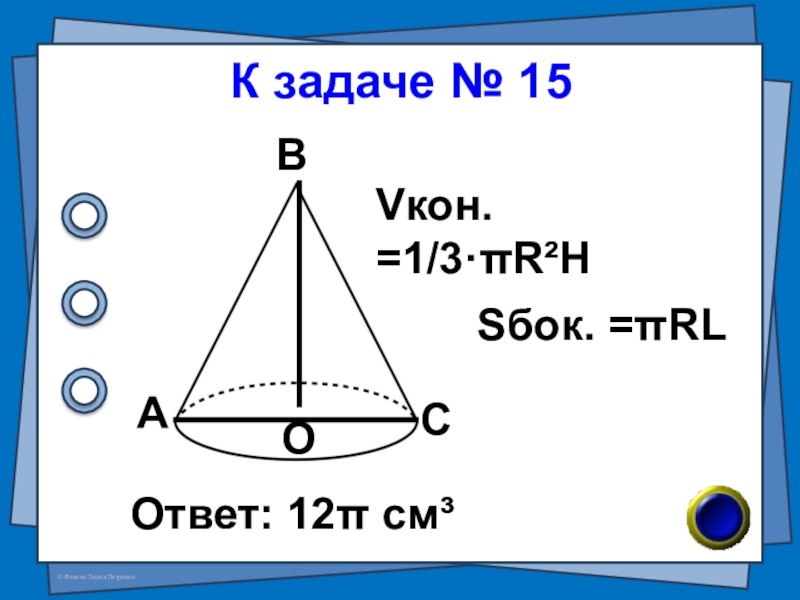
- 20. № 15 (В-62 №7)Образующая конуса равна 5см,
- 21. К задаче № 15Ответ: 12π см³АВСОVкон. =1/3·πR²HSбок. =πRL
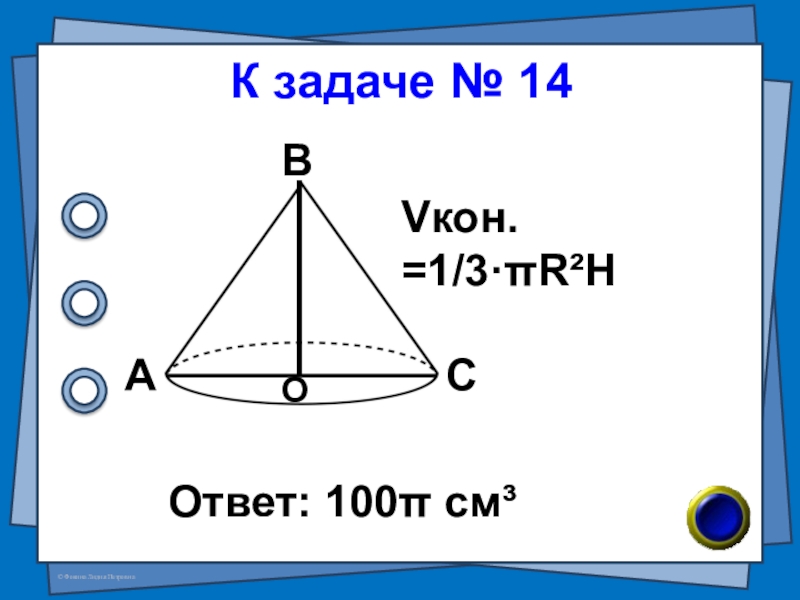
- 22. № 14 (В-60 №7)Радиус основания конуса
- 23. К задаче № 14Ответ: 100π см³АВСОVкон. =1/3·πR²H
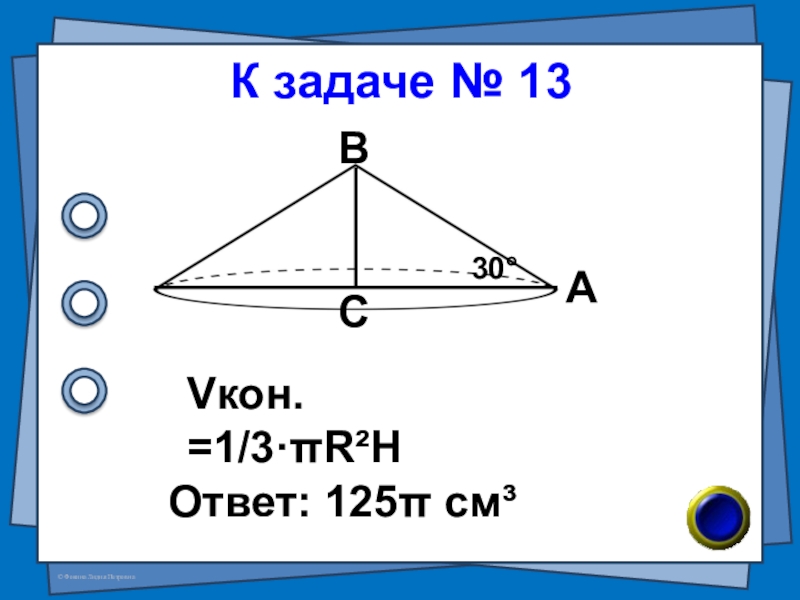
- 24. № 13 (В-51 №7)Найдите объём тела, полученного
- 25. К задаче № 13Ответ: 125π см³АВС30°Vкон. =1/3·πR²H
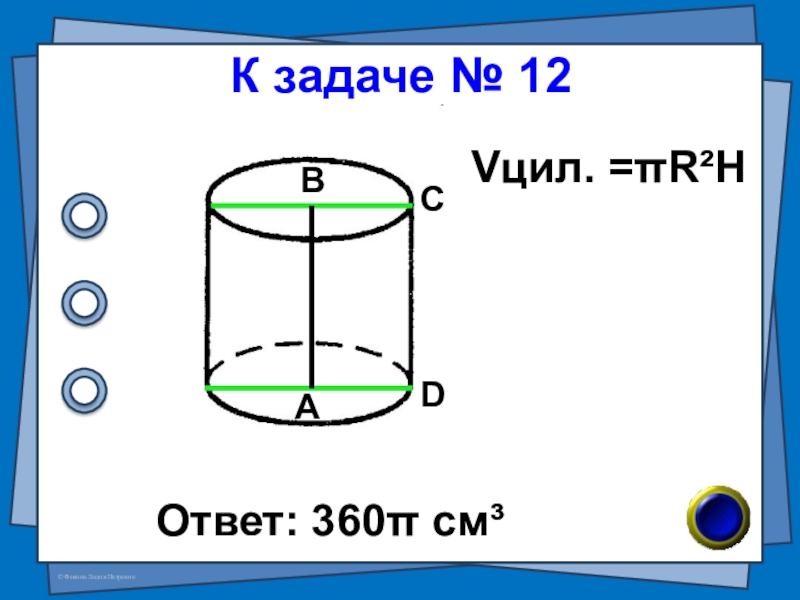
- 26. № 12 (В-48 №7) Найдите объём
- 27. К задаче № 12Ответ: 360π см³АВСDVцил. =πR²H
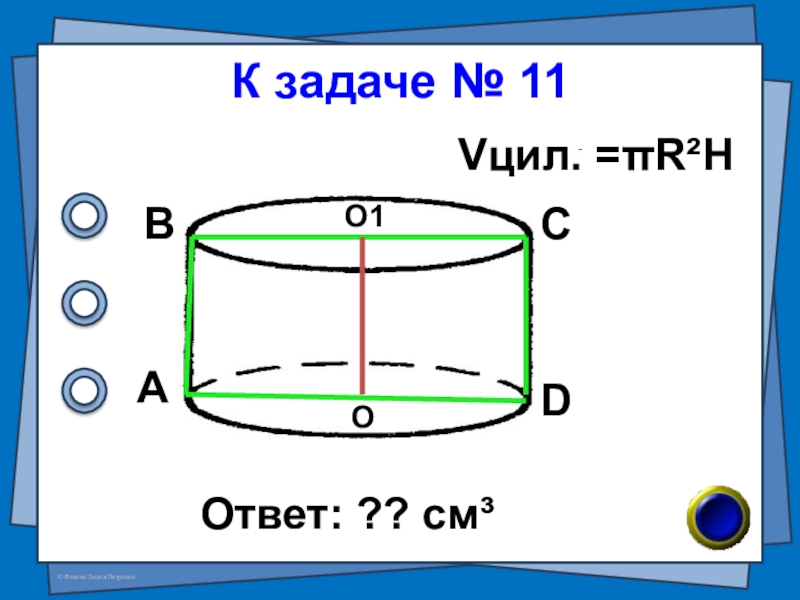
- 28. № 11 (В- 41 №7) Найдите объём
- 29. К задаче № 11Ответ: ?? см³АВСDОО1Vцил. =πR²H
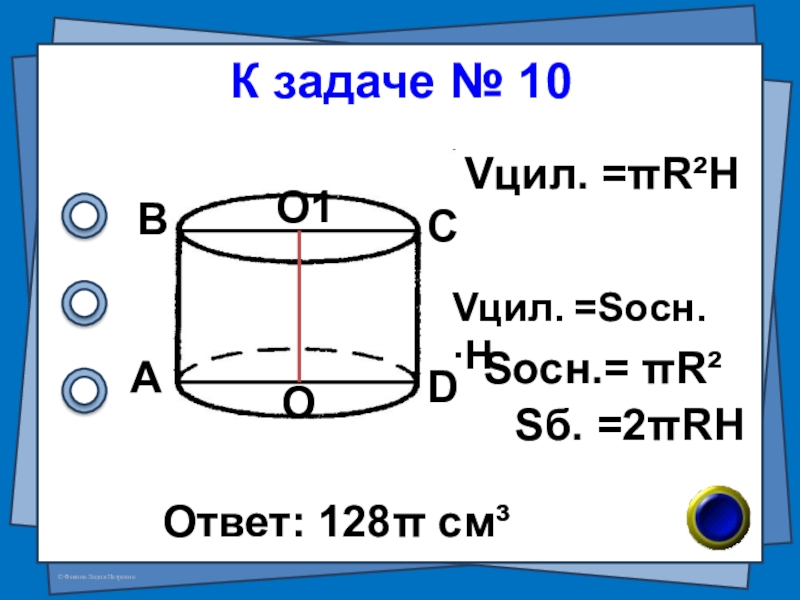
- 30. № 10 (В – 37 №7)
- 31. К задаче № 10Ответ: 128π см³АВСОО1DVцил. =πR²HVцил. =Sосн.·HSосн.= πR² Sб. =2πRH
- 32. (В-29 №7) Образующая конуса равна 12 см
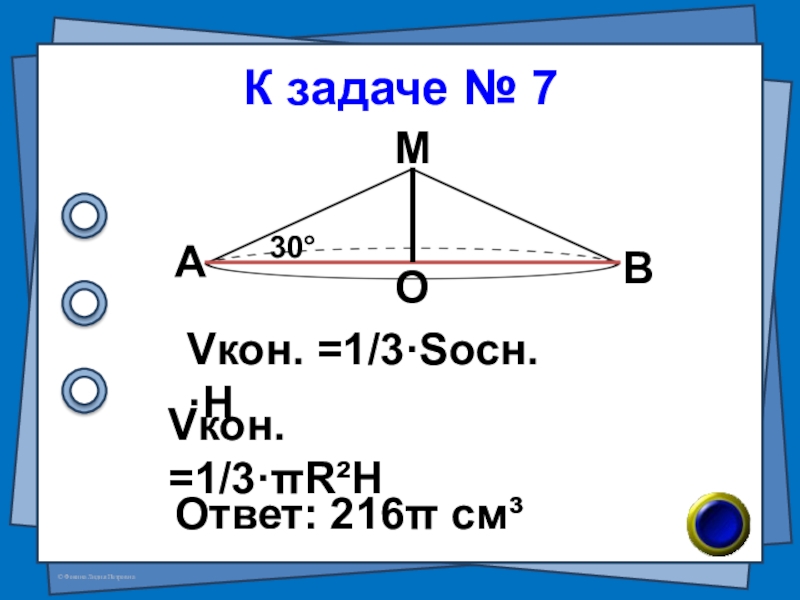
- 33. К задаче № 7Ответ: 216π см³АВОМ30°Vкон. =1/3·πR²HVкон. =1/3·Sосн.·H
- 34. (В-32 №7) Объём конуса с радиусом 6
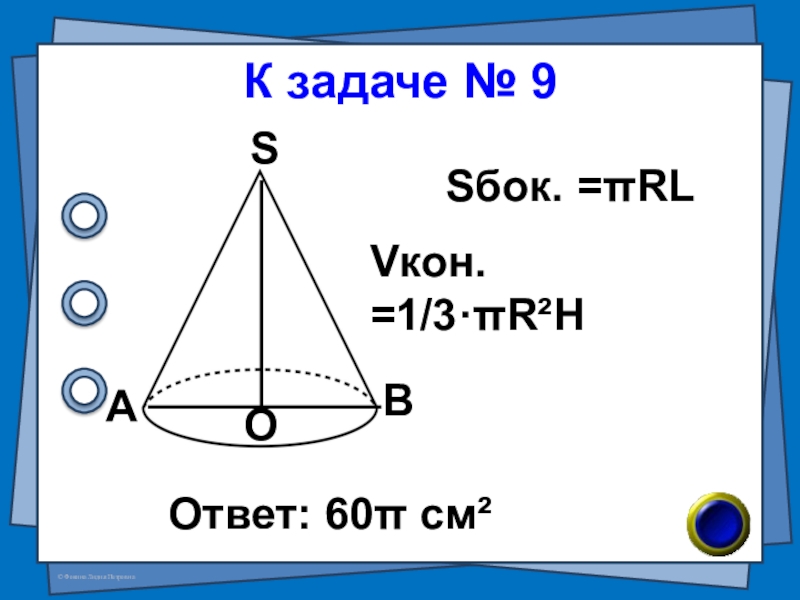
- 35. К задаче № 9Ответ: 60π см²АВОSSбок. =πRLVкон. =1/3·πR²H
- 36. (В – 68 №7) Квадрат со
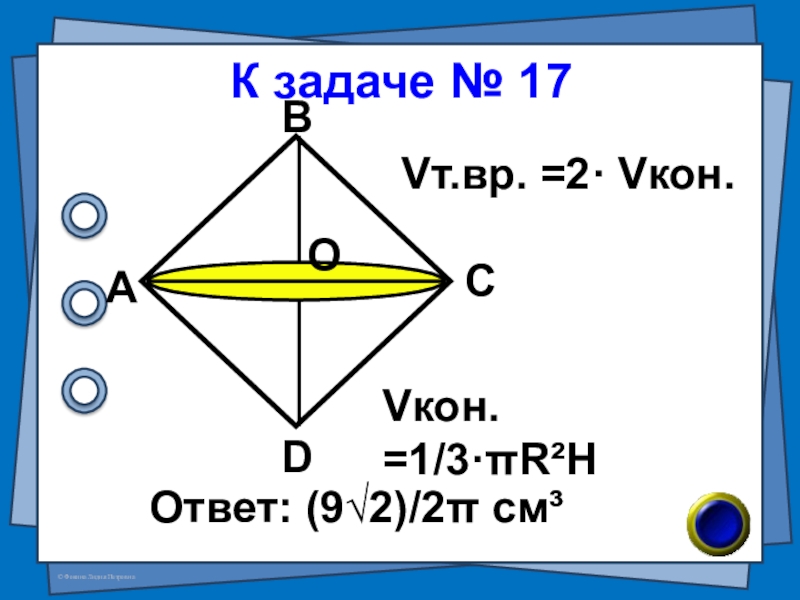
- 37. К задаче № 17Ответ: (9√2)/2π см³АВСDОVкон. =1/3·πR²HVт.вр. =2· Vкон.
- 38. (В-84 №7) Шар с
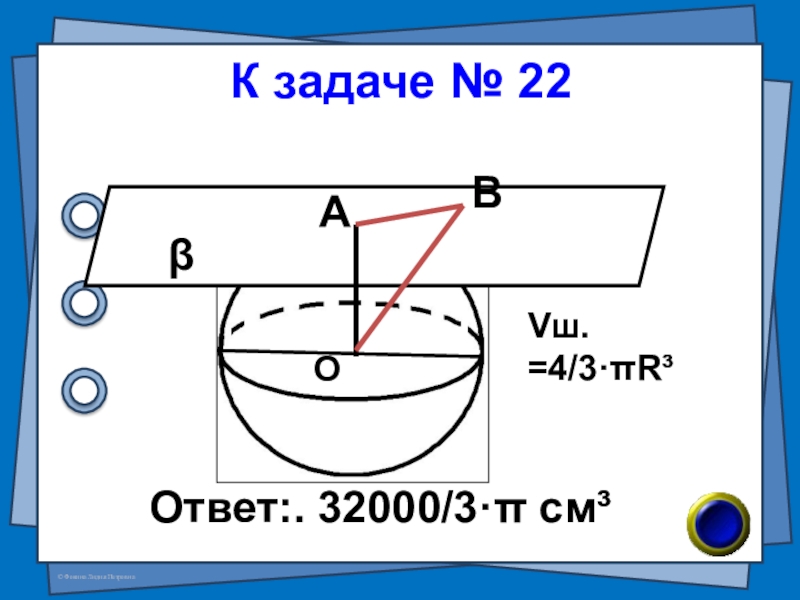
- 39. К задаче № 22Ответ:. 32000/3·π см³АВОβVш. =4/3·πR³
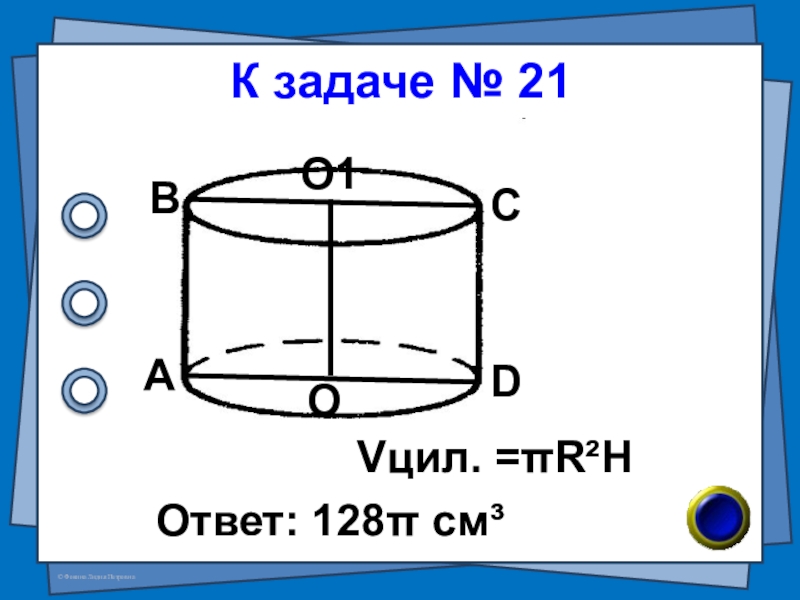
- 40. № 21 (В-82 №7)Площадь осевого сечения цилиндра
- 41. К задаче № 21Ответ: 128π см³АВСDОО1Vцил. =πR²H
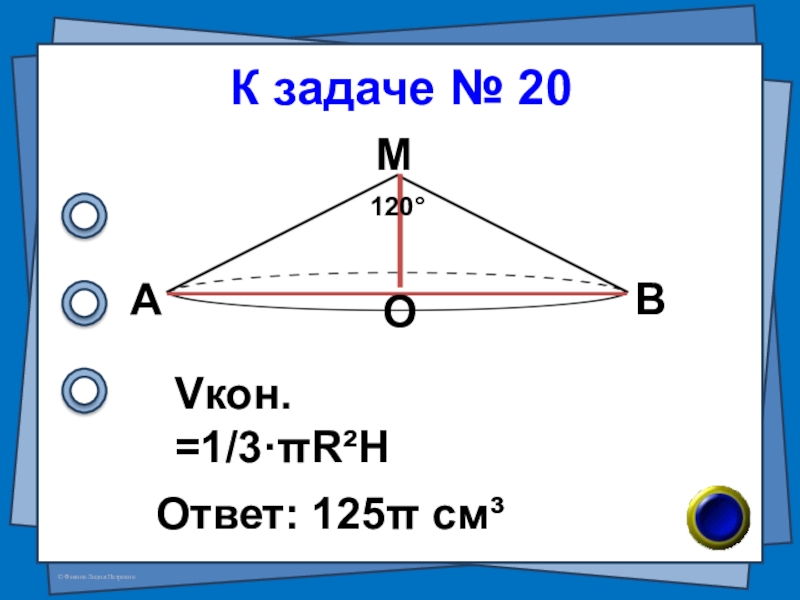
- 42. № 20 (В-78 №7) Высота конуса равна
- 43. К задаче № 20Ответ: 125π см³АВМО120°Vкон. =1/3·πR²H
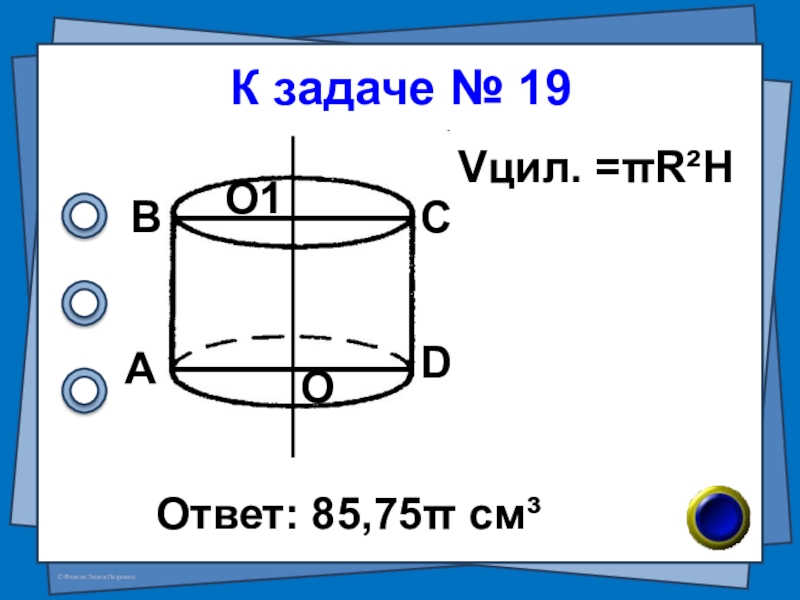
- 44. № 19 (В-70 №7)Найдите объём тела, полученного
- 45. К задаче № 19Ответ: 85,75π см³АВСDОО1Vцил. =πR²H
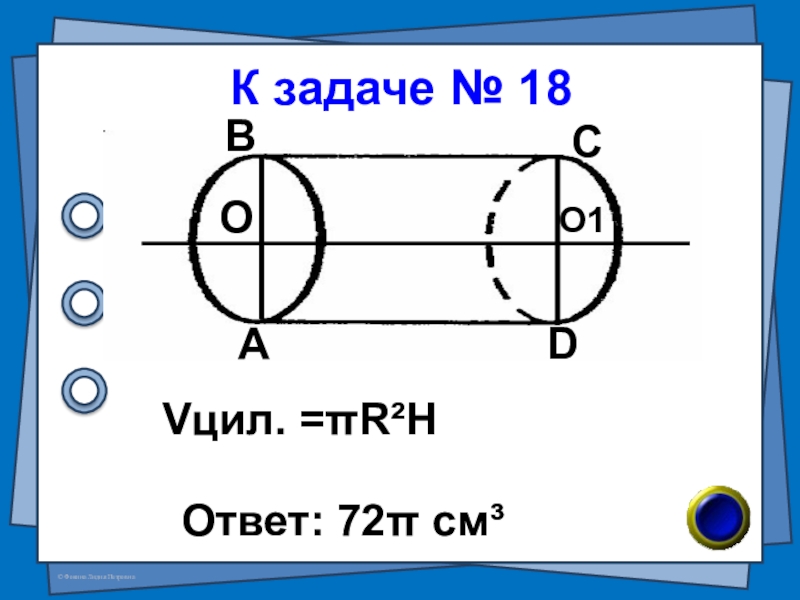
- 46. № 18 (В-69 №7)Найдите объём тела, полученного
- 47. К задаче № 18Ответ: 72π см³АВСDОО1Vцил. =πR²H
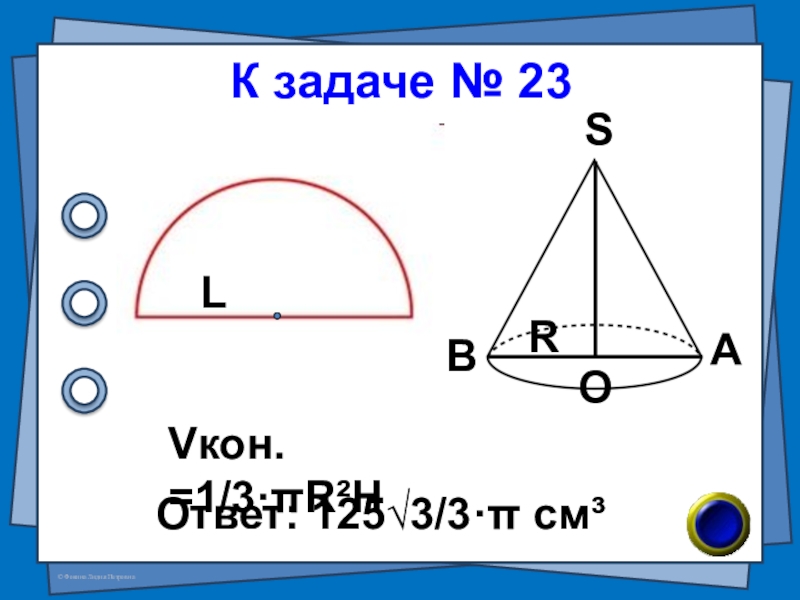
- 48. (В-85 №7) Полукруг свернут
- 49. К задаче № 23Ответ: 125√3/3·π см³АВОSVкон. =1/3·πR²HLR
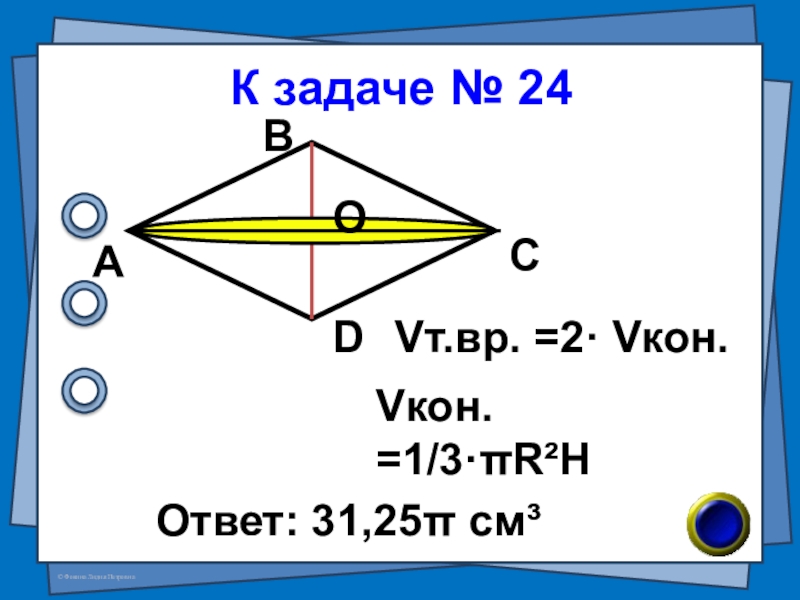
- 50. (В-88 №7) Ромб со стороной 5см
- 51. К задаче № 24Ответ: 31,25π см³АВСDОVкон. =1/3·πR²HVт.вр. =2· Vкон.
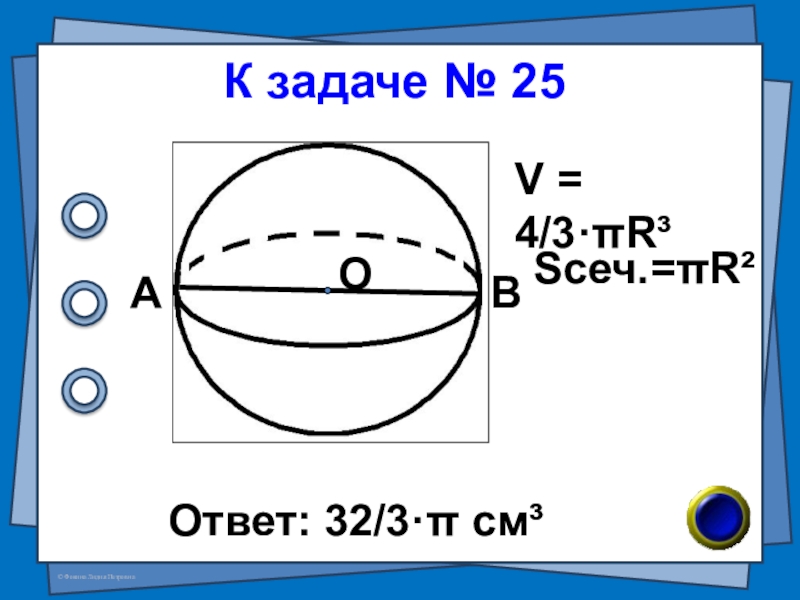
- 52. № 25 (В-89 №7)Площадь сечения шара плоскостью,
- 53. К задаче № 25Ответ: 32/3·π см³АВОV = 4/3·πR³Sсеч.=πR²
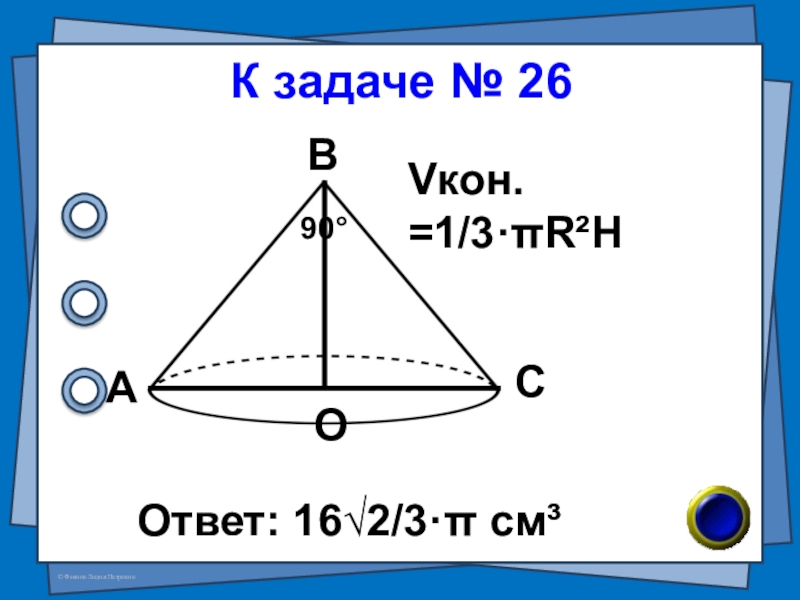
- 54. № 26 (В-91 №7)Образующая конуса равна 4см,
- 55. К задаче № 26Ответ: 16√2/3·π см³АВСО90°Vкон. =1/3·πR²H
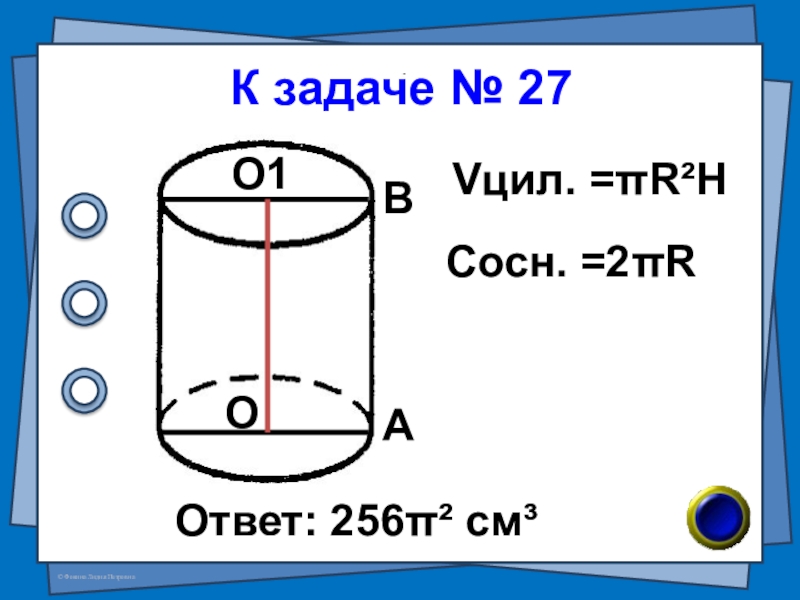
- 56. № 27 (в-96 №7)Радиус основания цилиндра равен
- 57. К задаче № 27Ответ: 256π² см³АВОО1Vцил. =πR²HСосн. =2πR
- 58. Дополнительные задачи на вычисление объёмов многогранников
- 59. (В-23 №7) Основание пирамиды – прямоугольник
- 60. (В-56 №7) Площадь полной поверхности прямоугольного параллелепипеда
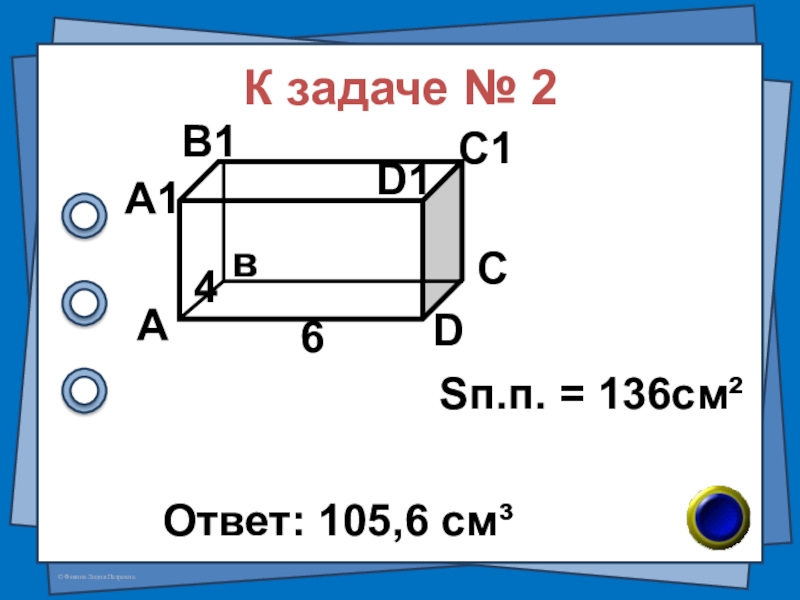
- 61. К задаче № 2Ответ: 105,6 см³АвСDА1В1С1D146Sп.п. = 136см²
- 62. (В-95 №7) В правильной четырехугольной пирамиде сторона
- 63. (В-24 №7) Основание пирамиды – ромб с
- 64. Используемые ресурсыЛ.С. Атанасян, В.Ф. Бутузов и др.
- 65. Используемые ресурсыУсеченный конус:Сфера (шар):Автор шаблона: Фокина Лидия
Повторение От арбуза радиусом 15 см отрезали верхушку (шапочку) толщиной 6 см. Каков радиус окружности на срезе?Решение.Ответ: 12 см
Слайд 1УМК: Л.С. Атанасян и др.
11 класс
Задачи по теме
«Тела вращения»
на вычисление объёмов
Слайд 2Повторение
От арбуза радиусом 15 см отрезали верхушку (шапочку) толщиной 6
см. Каков радиус окружности на срезе?
Решение.
Ответ: 12 см
Слайд 6№ 5 (В-18 №7)
Осевым сечением цилиндра является квадрат, диагональ которого
равна 8√2 см.Найдите объем цилиндра.
Слайд 8№4 (В-13 №7)
Найдите объём тела, полученного при вращении прямоугольного
треугольника с катетом 6см и гипотенузой 10см вокруг большего катета.
Слайд 10№ 3 (В-9 №7)
Найдите объём тела, полученного при вращении прямоугольного
треугольника с катетом 3см и прилежащим углом 30° вокруг меньшего катета.
Слайд 12№ 2 (В-4 №7)
Радиус основания цилиндра равен 4см, площадь боковой
поверхности вдвое больше площади основания. Найдите объём цилиндра.
Слайд 14№ 1
Равнобедренная трапеция, основания которой равны
6 см и 10 см,
а острый угол 60°, вращается вокруг большего основания. Найдите объем тела вращения.
Слайд 16№ 8 (В-31 №7)
Площадь боковой поверхности конуса равна 20π см², а
площадь его основания на
4π см² меньше. Найдите объём конуса.
4π см² меньше. Найдите объём конуса.
Слайд 18№ 16 (В-63 №7)
Высота цилиндра равна 6см, а его площадь боковой
поверхности вдвое меньше площади его полной поверхности. Найдите объём цилиндра.
Слайд 20№ 15 (В-62 №7)
Образующая конуса равна 5см, а площадь его боковой
поверхности равна 15π². Найдите объём конуса.
Слайд 22№ 14 (В-60 №7)
Радиус основания конуса равен 5 см, а
образующая конуса равна 13 см. найдите объём конуса.
Слайд 24№ 13 (В-51 №7)
Найдите объём тела, полученного при вращении прямоугольного треугольника
с гипотенузой 10см и острым углом 30° вокруг меньшего катета.
Слайд 26№ 12 (В-48 №7)
Найдите объём тела, полученного при вращении прямоугольника
со сторонами 6см и 10см вокруг большей стороны.
Слайд 28№ 11 (В- 41 №7)
Найдите объём тела, полученного при вращении
прямоугольника со сторонами 4см и 6см вокруг прямой, проходящей через середины его больших сторон.
Слайд 30№ 10 (В – 37 №7)
Радиус основания цилиндра равен 8см,
площадь боковой поверхности вдвое меньше площади основания. Найдите объём цилиндра.
Слайд 32(В-29 №7) Образующая конуса равна 12 см и составляет с плоскостью основания
угол в 30°. Найдите объём конуса.
№ 7
Слайд 34(В-32 №7) Объём конуса с радиусом 6 см равен 96π см³. Найдите
площадь боковой поверхности конуса.
№ 9
Слайд 36 (В – 68 №7) Квадрат со стороной 3см вращается вокруг своей
диагонали. Найдите объём тела вращения.
№ 17
Слайд 38 (В-84 №7) Шар с центром в точке О касается плоскости
в точка А. Точка В лежит в плоскости касания. Найдите объём шара, если АВ=21см, ВО=29см.
№ 22
Слайд 40№ 21 (В-82 №7)
Площадь осевого сечения цилиндра равна 64см², а его
образующая равна диаметру основания. Найдите объём цилиндра.
Слайд 42№ 20 (В-78 №7)
Высота конуса равна 5см, а угол при
вершине осевого сечения равен 120°. Найдите объём конуса.
Слайд 44№ 19 (В-70 №7)
Найдите объём тела, полученного при вращении квадрата со
стороной 7см вокруг прямой, соединяющей середины противолежащих сторон.
Слайд 46№ 18 (В-69 №7)
Найдите объём тела, полученного при вращении прямоугольника со
сторонами 6см и 8см вокруг прямой, которая проходит через середины его меньших сторон.
Слайд 48 (В-85 №7) Полукруг свернут в виде боковой поверхности конуса. Радиус
основания конуса 5см. Найдите объём конуса.
№ 23
Слайд 50 (В-88 №7) Ромб со стороной 5см и углом 60° вращается вокруг
своей меньшей диагонали. Определите объём тела вращения.
№ 24
Слайд 52№ 25 (В-89 №7)
Площадь сечения шара плоскостью, проходящей через его центр,
равна
4π см². Найдите объём шара.
4π см². Найдите объём шара.
Слайд 54№ 26 (В-91 №7)
Образующая конуса равна 4см, а угол при вершине
осевого сечения равен 90°. Найдите объём конуса.
Слайд 56№ 27 (в-96 №7)
Радиус основания цилиндра равен 4см, высота в два
раза больше длины окружности основания. Найдите объём цилиндра.
Слайд 59 (В-23 №7) Основание пирамиды – прямоугольник со сторонами 6см и 8см. Все
боковые рёбра равны 13см. Найдите объём пирамиды.
№ 1
Ответ: 192 см³
Слайд 60(В-56 №7) Площадь полной поверхности прямоугольного параллелепипеда равна 136 см², стороны основания
4см и 6см. Вычислите объём прямоугольного параллелепипеда.
№ 2
Слайд 62(В-95 №7) В правильной четырехугольной пирамиде сторона основания равна 8см, а боковое
ребро наклонено к плоскости основания под углом 45°. Найдите объём пирамиды.
№ 3
Ответ: 256√2/3 см³
Слайд 63(В-24 №7) Основание пирамиды – ромб с диагоналями 6см и 8см. Высота
пирамиды опущена в точку пересечения его диагоналей. Меньшие боковые рёбра пирамиды равны 5см. Найдите объем пирамиды.
№ 4
Ответ: 32 см³
Слайд 64Используемые ресурсы
Л.С. Атанасян, В.Ф. Бутузов и др. Геометрия. 10-11 классы: учебник
для общеобразоват. Учреждений: базовый и профильный уровни – М.: Просвещение, 2013
Г.В. Дорофеев. Сборник заданий для проведения письменного экзамена по математике за курс средней школы 11 класс. – М., Дрофа, 2002
Цилиндр:
Конус:
Г.В. Дорофеев. Сборник заданий для проведения письменного экзамена по математике за курс средней школы 11 класс. – М., Дрофа, 2002
Цилиндр:
Конус:
http://cummins-vrn.ru/labraries/image/aHR0cDovLzkwMGlnci5uZXQvZGF0YXMvZ2VvbWV0cmlqYS9WcGlzYW5ueWotdWdvbC8wMDIyLTAyMi1SZXNoZW5pZS5qcGc
http://5terka.com/images/atan1011geom/atan1011reshf2-62.png
http://belmathematics.by.swtest.ru/images/teorija/cilindr.jpg
http://belmathematics.by.swtest.ru/images/teorija/konys.jpg
http://terka.su/wp-content/uploads/2015/1/terka-konus-gc-ca01_1.gif
Слайд 65Используемые ресурсы
Усеченный конус:
Сфера (шар):
Автор шаблона: Фокина Лидия Петровна, учитель начальных классов
МКОУ «СОШ ст. Евсино» Искитимского района
Новосибирской области
Новосибирской области
http://board.salle.com.ua/i/2016/20168/645278_2014011124.jpg
http://izlov.ru/tw_files2/urls_1/3/d-2906/2906_html_773423cd.png
http://dic.academic.ru/pictures/es/285211.jpg
http://player.myshared.ru/587947/data/images/img11.jpg
http://superwave.ru/files/polygraphy/small/271_articules200x160c3.jpg
