- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Второй и третий признаки равенства треугольников
Содержание
- 1. Второй и третий признаки равенства треугольников
- 2. Второй признак равенства треугольников.Если сторона и два
- 3. АВСВ₁С₁А₁Наложим ∆АВС на А₁В₁С₁, так чтобы вершина
- 4. Слайд 4
- 5. ЗадачаАCDBДано:АСВ=ACD,АС-биссектриса ВAD.Доказать: ∆АВС=∆АDСДоказательство:АС – (какая?)2. АСВ=ACD (почему?).3.
- 6. Третий признак равенства треугольников.Если три стороны одного
- 7. Слайд 7
- 8. ЗадачаДано: МЕ=ЕС; МР=РСДоказать: Доказательство:1. МЕ=ЕС (почему?); 2. МР=РС(почему?)3. РЕ – (какая?)Значит, (почему?)
- 9. При подготовке данного урока был использована следующая
Второй признак равенства треугольников.Если сторона и два прилегающих к ней угла одного треугольника соответственно равны стороне и двум прилегающим к ней углам другого треугольника, то такие треугольники равны.Дано:∆ АВС и ∆ А₁В₁С₁АС=А₁С₁; А=А₁; В=В₁.Доказать, что
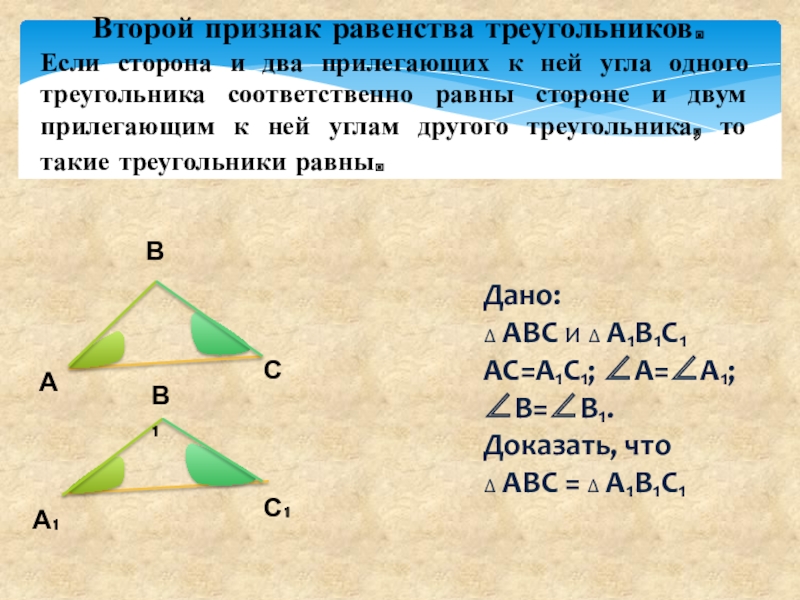
Слайд 2Второй признак равенства треугольников.
Если сторона и два прилегающих к ней угла
одного треугольника соответственно равны стороне и двум прилегающим к ней углам другого треугольника, то такие треугольники равны.
Дано:
∆ АВС и ∆ А₁В₁С₁
АС=А₁С₁; А=А₁; В=В₁.
Доказать, что ∆ АВС = ∆ А₁В₁С₁
А
С
В
С₁
А₁
В₁
Слайд 3А
В
С
В₁
С₁
А₁
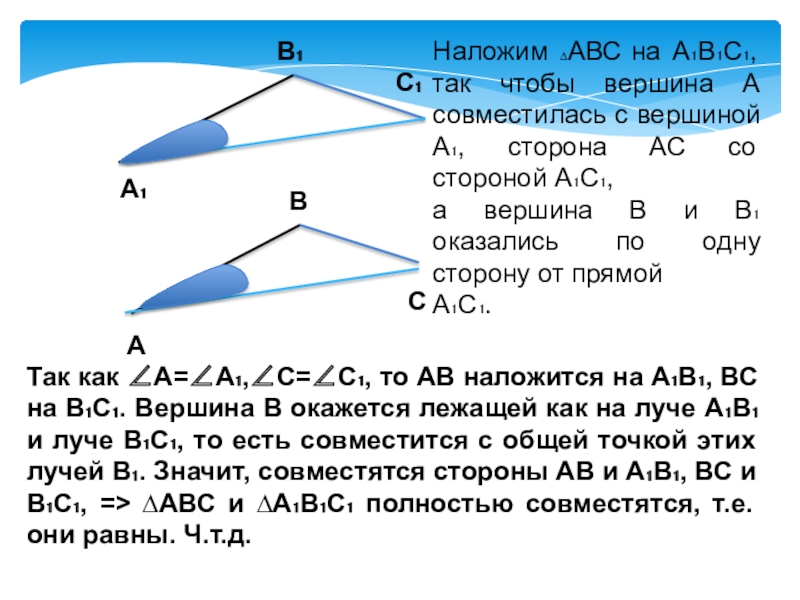
Наложим ∆АВС на А₁В₁С₁, так чтобы вершина А совместилась с вершиной
А₁, сторона АС со стороной А₁С₁,
а вершина В и В₁ оказались по одну сторону от прямой
А₁С₁.
а вершина В и В₁ оказались по одну сторону от прямой
А₁С₁.
Так как А=А₁,С=С₁, то АВ наложится на А₁В₁, ВС на В₁С₁. Вершина В окажется лежащей как на луче А₁В₁ и луче В₁С₁, то есть совместится с общей точкой этих лучей В₁. Значит, совместятся стороны АВ и А₁В₁, ВС и В₁С₁, => ∆АВС и ∆А₁В₁С₁ полностью совместятся, т.е. они равны. Ч.т.д.
Слайд 5Задача
А
C
D
B
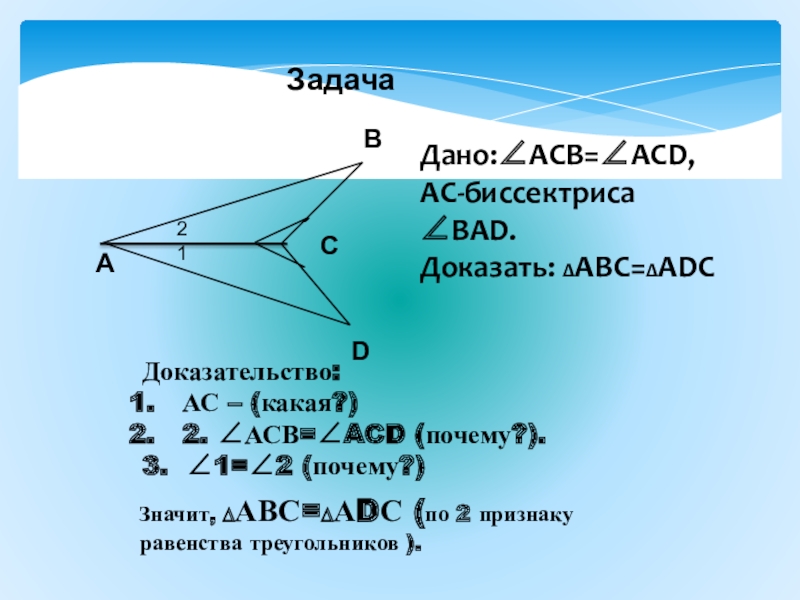
Дано:АСВ=ACD,
АС-биссектриса ВAD.
Доказать: ∆АВС=∆АDС
Доказательство:
АС – (какая?)
2. АСВ=ACD (почему?).
3. 1=2 (почему?)
1
2
Значит, ∆АВС=∆АDС
(по 2 признаку
равенства треугольников ).
равенства треугольников ).
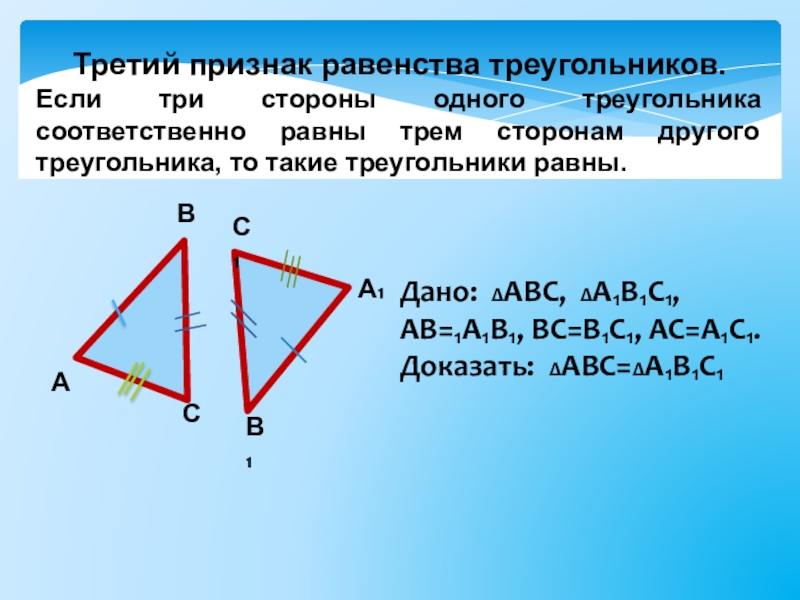
Слайд 6Третий признак равенства треугольников.
Если три стороны одного треугольника соответственно равны трем
сторонам другого треугольника, то такие треугольники равны.
В
А
С
С₁
А₁
В₁
Дано: ∆АВС, ∆А₁В₁С₁,
АВ=₁А₁В₁, ВС=В₁С₁, АС=А₁С₁.
Доказать: ∆АВС=∆А₁В₁С₁
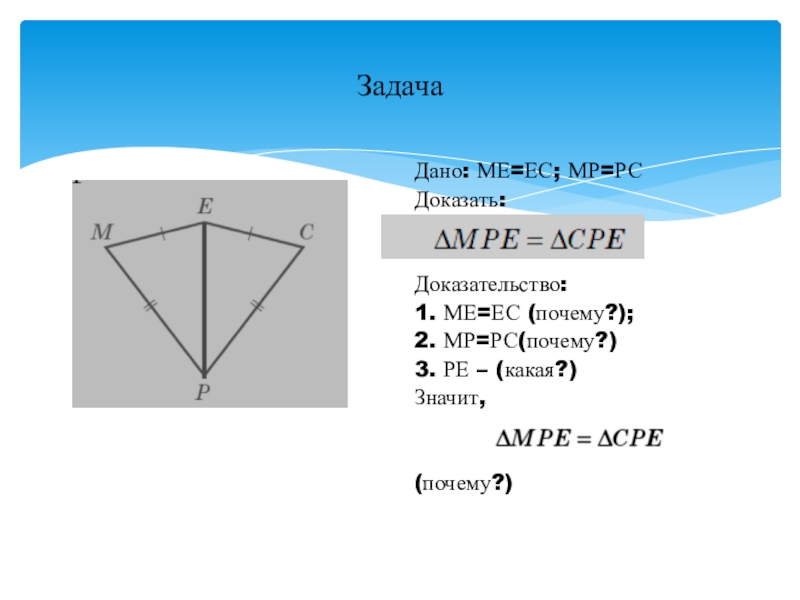
Слайд 8Задача
Дано: МЕ=ЕС; МР=РС
Доказать:
Доказательство:
1. МЕ=ЕС (почему?);
2. МР=РС(почему?)
3. РЕ – (какая?)
Значит,
(почему?)
Слайд 9При подготовке данного урока был использована
следующая литература:
Л.С.Атанасян «Геометрия, 7-9: Учеб.
для общеобразовательных
учреждений. – М.: Просвещение, 2004.
учреждений. – М.: Просвещение, 2004.
