Никонова Галина Михайловна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Виды движений (11 класс)
Содержание
- 1. Виды движений (11 класс)
- 2. Симметрия – это идея, с помощью которой
- 3. История Симметрии.Однако как люди дошли до такой
- 4. Принципы симметрии играют важную роль в физике
- 5. Движение. Виды движения. Движение плоскости – это
- 6. ОСЕВАЯ СИММЕТРИЯ.Преобразование, при котором каждая точка А
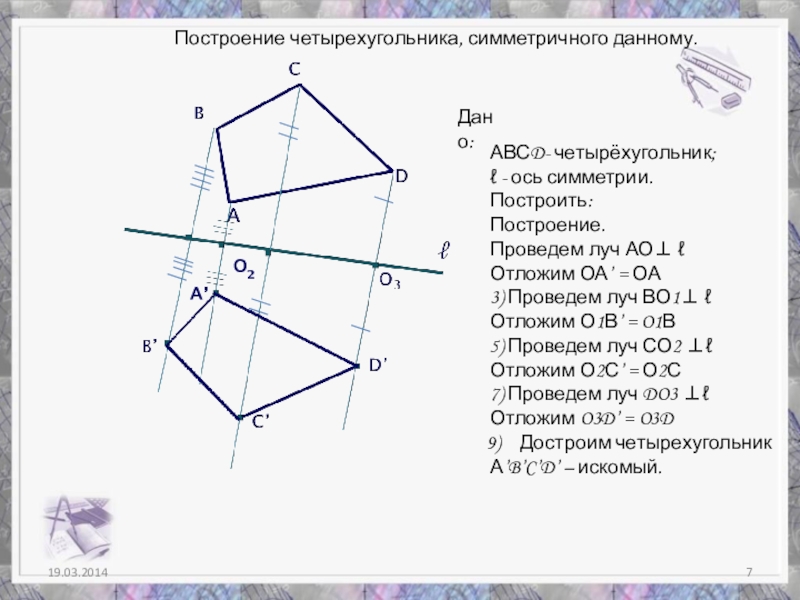
- 7. О2 А’Дано:АВСD- четырёхугольник;ℓ - ось симметрии.Построить:Построение.Проведем луч
- 8. Построение отрезка, симметричного данномуАсА’ВВ’OO'АА’с, АО=ОА’.ВВ’с, ВО’=О’В’.3. А’В’ – искомый отрезок.
- 9. Фигуры, имеющие две оси симметрии.Прямоугольник и ромб, не являющиеся квадратами, имеют две оси симметрии
- 10. Построение точки, центрально симметричной данной....АА’ОПреобразование, переводящее
- 11. Дано:
- 12. СКОЛЬЗЯЩАЯ СИММЕТРИЯ.Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.
- 13. Примером является орнамент – бордюр.
- 14. Винтовая симметрия – это поворот и перенос одновременно.У раковины моллюска - винтовая симметрия.
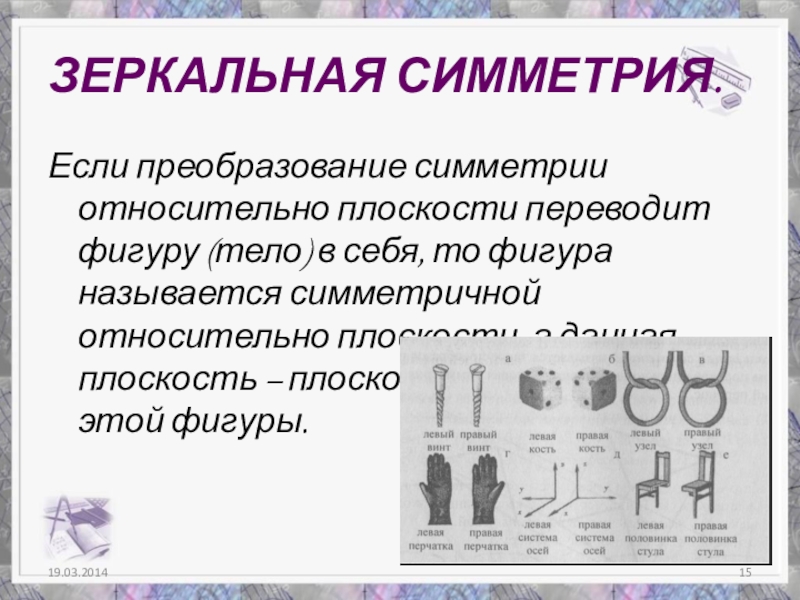
- 15. ЗЕРКАЛЬНАЯ СИММЕТРИЯ.Если преобразование симметрии относительно плоскости переводит
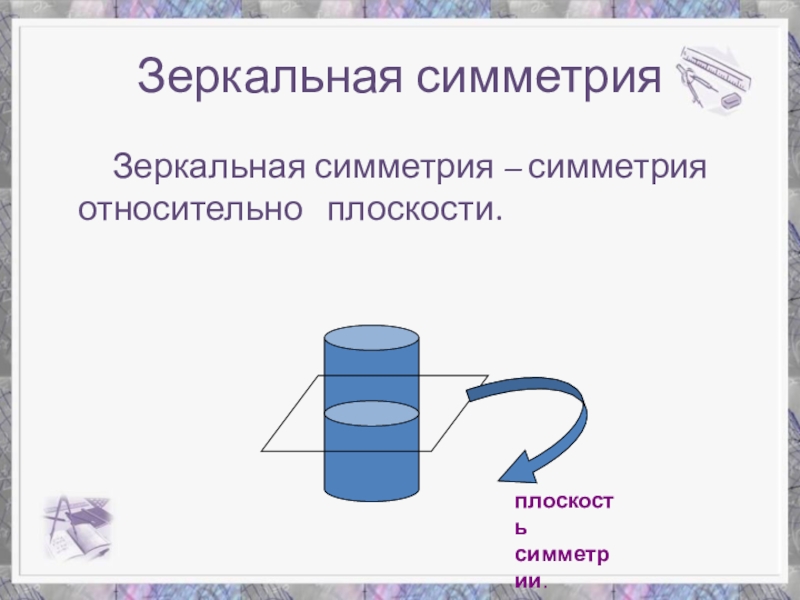
- 16. Зеркальная симметрия Зеркальная симметрия – симметрия относительно плоскости.плоскость симметрии.
- 17. Поворот вокруг точки.Поворотом точки А вокруг
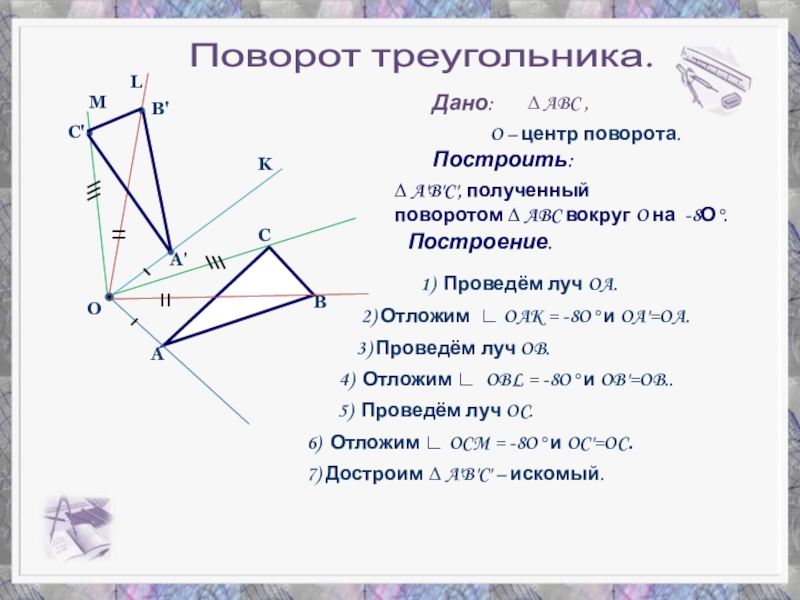
- 18. Дано:ABCOA'B'C'MLK∆ ABC ,O – центр поворота.∆ A'B'C',
- 19. ПАРАЛЛЕЛЬНЫЙ ПЕРНОС.Преобразование, при котором каждая точка
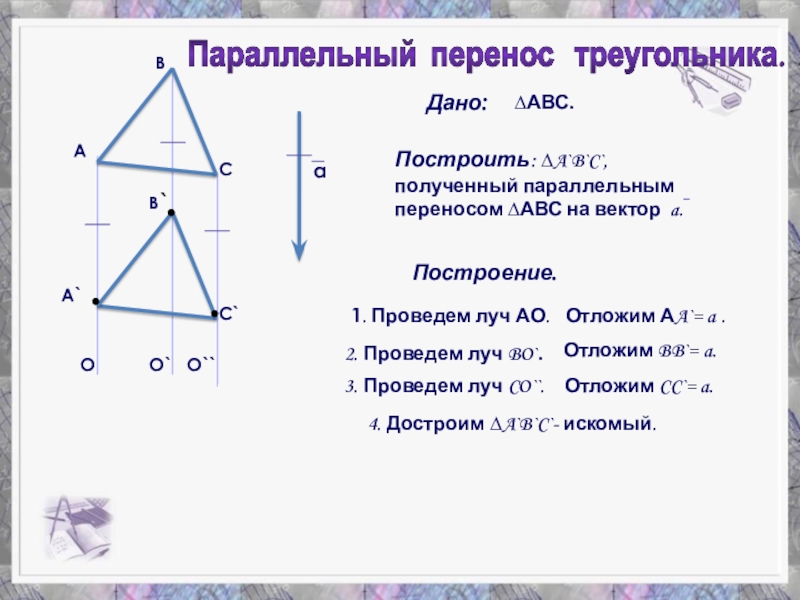
- 20. АВСaA`B`C`Дано:∆АВС.Построить: ∆A`B`C`, полученный параллельным переносом ∆АВС на
- 21. Геометрические фигуры, имеющие центр симметрии.Многие фигуры
- 22. Центр окружности (или круга) является центром его
- 23. Центр симметрии имеют также:ромбпараллелограммправильный
- 24. Геометрические фигуры, имеющие ось симметрии.К фигурам,
- 25. Ось симметрии окружности (или круга) – прямая,
- 26. Ось симметрии равнобедренного треугольника – прямая, содержащая
- 27. Ось симметрии равнобокой трапеции – прямая, проходящая
- 28. Фигуры, не обладающие центральной симметриейНеправильный многоугольникПроизвольный треугольникУголтрапеция
- 29. Примеры вышеупомянутых видов симметрии .Шар ( сфера ) обладает и
- 30. ВЕЛИКИЕ О СИММЕТРИИ…Термин «симметрия» придумал скульптор Пифагор
- 31. Леонардо да Винчи считал, что главную роль
- 32. Симметрия человекаКрасота человеческого тела обусловлена пропорциональностью и
- 33. Симметрия в природеСимметрия в нашем представлении тесно
- 34. Каждая снежинка – это маленький кристалл замерзшей
- 35. СИММЕТРИЯ В РАСТЕНИЯХ.Внимательное наблюдение показывает, что основу
- 36. Ромашка
- 37. СИММЕТРИЯ В ЖИВОТНОМ МИРЕ.Симметрия встречается и в
- 38. Симметрия в животном мире
- 39. СИММЕТРИЯ В АРХИТЕКТУРЕ.Нагляднее всего видна симметрия в
- 40. Казанский соборГостиница «Прибалтийская»
- 41. Пирамида Хеопса ЕгипетСобор Парижской Богоматери ФранцияТадж Махал ТурцияБиг Бэн ВеликобританияЭйфелева Башня
- 42. Симметрия в архитектуре РоссииКазанский собор Зимний ДворецОстанкинская башняКремльРазводной мост Исаакиевский Собор
- 43. Игорь Жаборовский
- 44. Слайд 44
- 45. Центральная симметрия в транспорте: Вид сверху и
- 46. Железнодорожный вокзал
- 47. СИММЕТРИЯ В ЛИТЕРАТУРЕВ литературных произведениях существует симметрия
- 48. СИММЕТРИЯ В РУССКОМ ЯЗЫКЕ. Буквы русского
- 49. В русском языке есть «симметричные слова –
- 50. СИММЕТРИЯ В ОРНАМЕНТАХПринцип симметрия используется в построении орнамента.Орнамент – узор, состоящий из повторяющихся, ритмически упорядоченных элементов.
- 51. Слайд 51
- 52. Оказывается, что без симметрии наш мир выглядел
- 53. Конец!Спасибо за просмотр!
Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство.
Слайд 1Презентация по математике
на тему: «Движение. Виды движения»
Выполнили:
Телешева Мария,
Демидович Анна
Учитель:
Слайд 2Симметрия – это идея, с помощью которой человек веками пытался объяснить
и создать порядок, красоту и совершенство.
Г. Вейль
Г. Вейль
Слайд 3История Симметрии.
Однако как люди дошли до такой сложной и одновременно такой
простой вещи, как симметрия?
Ещё древние греки считали, что симметрия – это гармония, соразмерность. Они же и ввели термин «симметрия».
А у древних народов, таких как шумеры и египтяне, у первобытных племён, да и у кое-кого в наше время симметрия ассоциируется не только с красотой и гармонией, но и прежде всего с магией. Не зря же люди в эпоху мегалита для ритуальных целей сооружали кромлихи в форме круга – «идеально симметричной» геометрической фигуры.
Ещё древние греки считали, что симметрия – это гармония, соразмерность. Они же и ввели термин «симметрия».
А у древних народов, таких как шумеры и египтяне, у первобытных племён, да и у кое-кого в наше время симметрия ассоциируется не только с красотой и гармонией, но и прежде всего с магией. Не зря же люди в эпоху мегалита для ритуальных целей сооружали кромлихи в форме круга – «идеально симметричной» геометрической фигуры.
Слайд 4Принципы симметрии играют важную роль в физике и математике, химии и
биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке.
Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, также подчиняются принципам симметрии.
Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, также подчиняются принципам симметрии.
Слайд 5Движение. Виды движения.
Движение плоскости – это отображение плоскости на себя, сохраняющее
расстояния.
Виды движения:
1. Симметрия:
─ осевая,
─ центральная,
─ скользящая.
─ зеркальная.
2. Параллельный перенос:
3. Поворот.
Виды движения:
1. Симметрия:
─ осевая,
─ центральная,
─ скользящая.
─ зеркальная.
2. Параллельный перенос:
3. Поворот.
Слайд 6ОСЕВАЯ СИММЕТРИЯ.
Преобразование, при котором каждая точка А фигуры (или тела) преобразуется
в симметричную ей относительно некоторой оси l точку А', называется осевой симметрией.
А’
А
Слайд 7О2
А’
Дано:
АВСD- четырёхугольник;
ℓ - ось симметрии.
Построить:
Построение.
Проведем луч АО⊥ ℓ
Отложим ОА’
= ОА
3) Проведем луч ВО1⊥ ℓ
Отложим О1В’ = O1В
5) Проведем луч СО2 ⊥ℓ
Отложим О2С’ = О2С
7) Проведем луч DO3 ⊥ℓ
Отложим O3D’ = O3D
Достроим четырехугольник
А’B’C’D’ – искомый.
3) Проведем луч ВО1⊥ ℓ
Отложим О1В’ = O1В
5) Проведем луч СО2 ⊥ℓ
Отложим О2С’ = О2С
7) Проведем луч DO3 ⊥ℓ
Отложим O3D’ = O3D
Достроим четырехугольник
А’B’C’D’ – искомый.
Построение четырехугольника, симметричного данному.
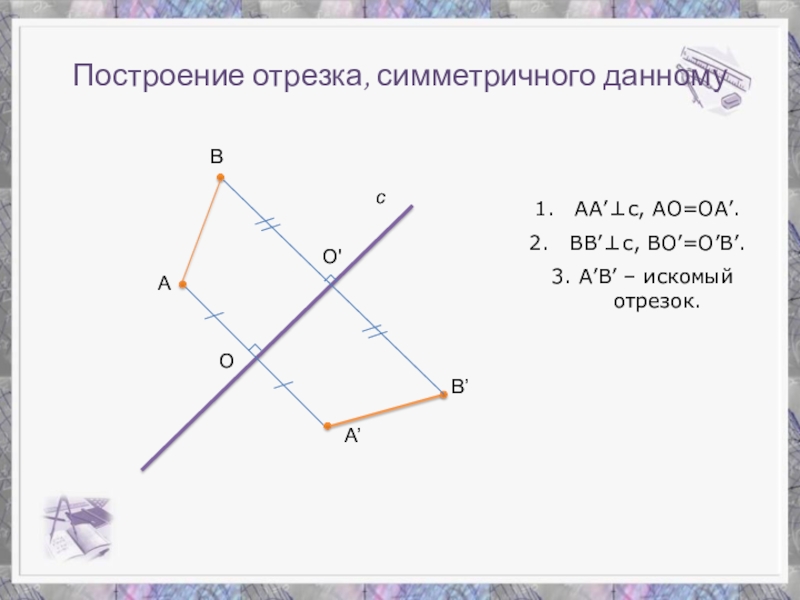
Слайд 8Построение отрезка, симметричного данному
А
с
А’
В
В’
O
O'
АА’с, АО=ОА’.
ВВ’с, ВО’=О’В’.
3. А’В’ – искомый отрезок.
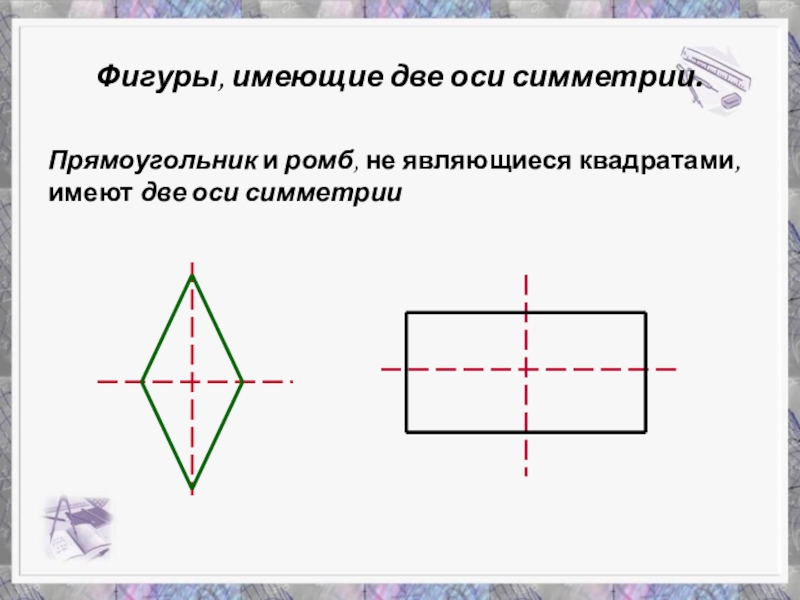
Слайд 9Фигуры, имеющие две оси симметрии.
Прямоугольник и ромб, не являющиеся квадратами, имеют
две оси симметрии
Слайд 10 Построение точки,
центрально симметричной данной.
.
.
.
А
А’
О
Преобразование, переводящее каждую точку А фигуры
(тела) в точку А', симметричную ей относительно центра О, называется преобразованием центральной симметрии или просто центральной симметрией.
3. Точка А1 – искомая.
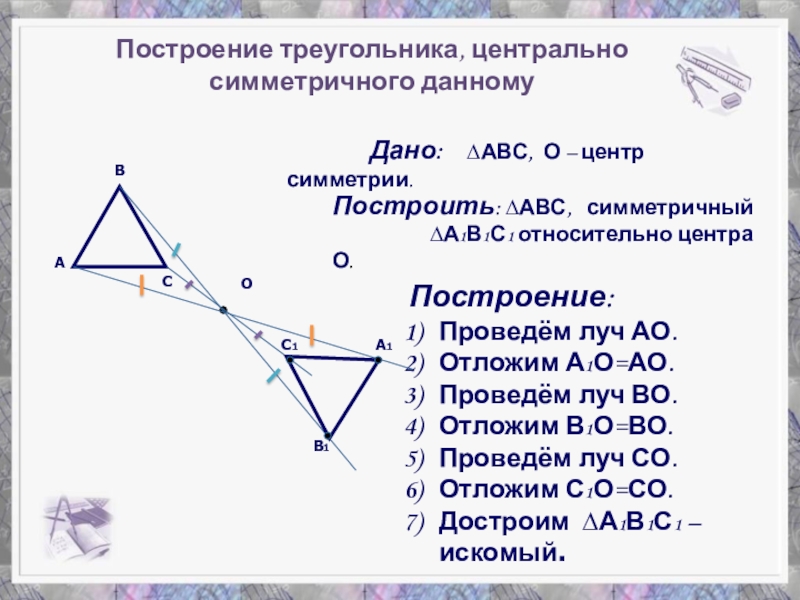
Слайд 11 Дано: ∆АВС, О –
центр симметрии.
О
А
В
С
Построение:
Проведём луч АО.
Отложим А1О=АО.
Проведём луч ВО.
Отложим В1О=ВО.
Проведём луч СО.
Отложим С1О=СО.
Достроим ∆А1В1С1 – искомый.
А1
В1
С1
Построить: ∆АВС, симметричный
∆А1В1С1 относительно центра О.
Построение треугольника, центрально симметричного данному
Слайд 12СКОЛЬЗЯЩАЯ СИММЕТРИЯ.
Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая
симметрия и параллельный перенос.
Слайд 14Винтовая симметрия – это поворот и перенос одновременно.
У раковины моллюска -
винтовая симметрия.
Слайд 15ЗЕРКАЛЬНАЯ СИММЕТРИЯ.
Если преобразование симметрии относительно плоскости переводит фигуру (тело) в себя,
то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры.
Слайд 16Зеркальная симметрия
Зеркальная симметрия – симметрия относительно
плоскости.
плоскость
симметрии.
Слайд 17
Поворот вокруг точки.
Поворотом точки А вокруг точки О на угол
α называется преобразование, при котором точка А переходит в точку А1 такую, что ОА = ОА1 и ∟АОА1 = α (О – центр поворота, α – угол поворота).
.
.
.
О
А
А1
α
О – центр поворота.
ОА = ОА1 ; ∟АОА1 = α.
Точка А1 получена из точки А поворотом вокруг точки О на угол α
Слайд 18Дано:
A
B
C
O
A'
B'
C'
M
L
K
∆ ABC ,
O – центр поворота.
∆ A'B'C', полученный
поворотом ∆ ABC
вокруг O на -8О°.
Построение.
1) Проведём луч OA.
2) Отложим ∟ OAK = -8O° и OA'=OA.
3) Проведём луч OB.
4) Отложим ∟ OBL = -8O° и OB'=OB..
5) Проведём луч OC.
6) Отложим ∟ OCM = -8O° и OC'=OC.
7) Достроим ∆ A'B'C' – искомый.
Построить:
Поворот треугольника.
Слайд 19 ПАРАЛЛЕЛЬНЫЙ ПЕРНОС.
Преобразование, при котором каждая точка фигуры (тела) перемещается в
одном и том же направлении на одно и то же расстояние, называется параллельным переносом.
Слайд 20А
В
С
a
A`
B`
C`
Дано:
∆АВС.
Построить: ∆A`B`C`, полученный параллельным переносом ∆АВС на вектор a.
Построение.
О
О`
O``
1. Проведем луч
АО.
Отложим АA`= a .
2. Проведем луч BO`.
Отложим BB`= a.
3. Проведем луч CO``.
Отложим CC`= a.
4. Достроим ∆A`B`C`- искомый.
.
.
.
Параллельный перенос треугольника.
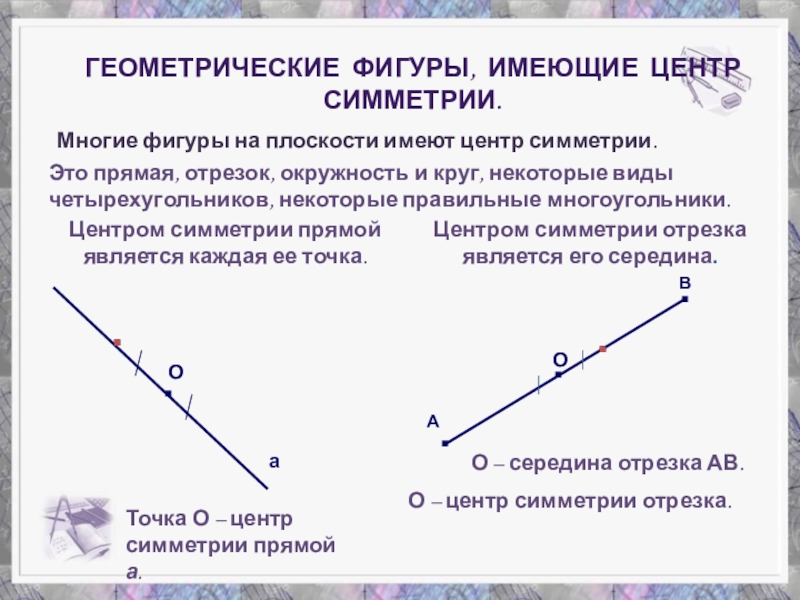
Слайд 21Геометрические фигуры, имеющие центр симметрии.
Многие фигуры на плоскости имеют центр
симметрии.
Это прямая, отрезок, окружность и круг, некоторые виды четырехугольников, некоторые правильные многоугольники.
Центром симметрии прямой является каждая ее точка.
.
.
.
.
.
О
Точка О – центр симметрии прямой а.
а
Центром симметрии отрезка является его середина.
А
В
О – середина отрезка АВ.
О – центр симметрии отрезка.
.
.
.
О
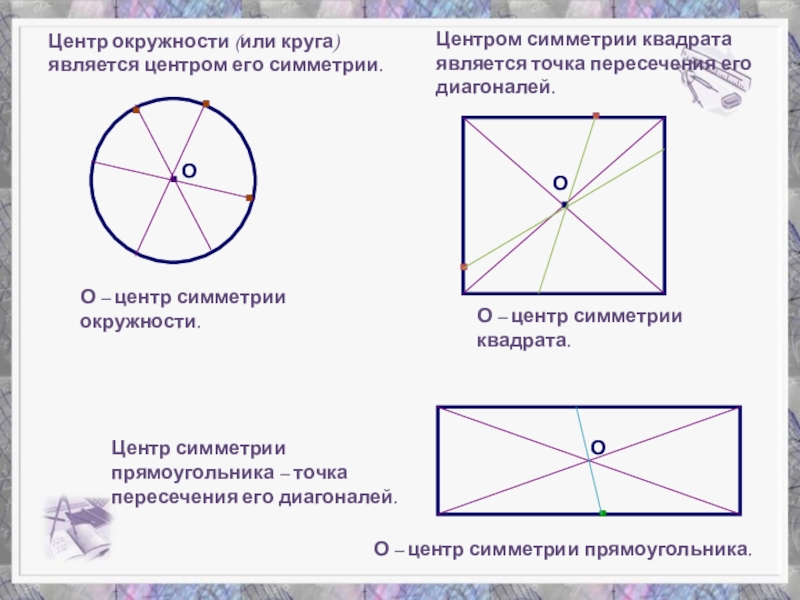
Слайд 22Центр окружности (или круга) является центром его симметрии.
.
О
.
.
.
.
.
.
О – центр симметрии
окружности.
Центром симметрии квадрата является точка пересечения его диагоналей.
О
.
.
.
.
О – центр симметрии квадрата.
.
Центр симметрии прямоугольника – точка пересечения его диагоналей.
О
.
.
О – центр симметрии прямоугольника.
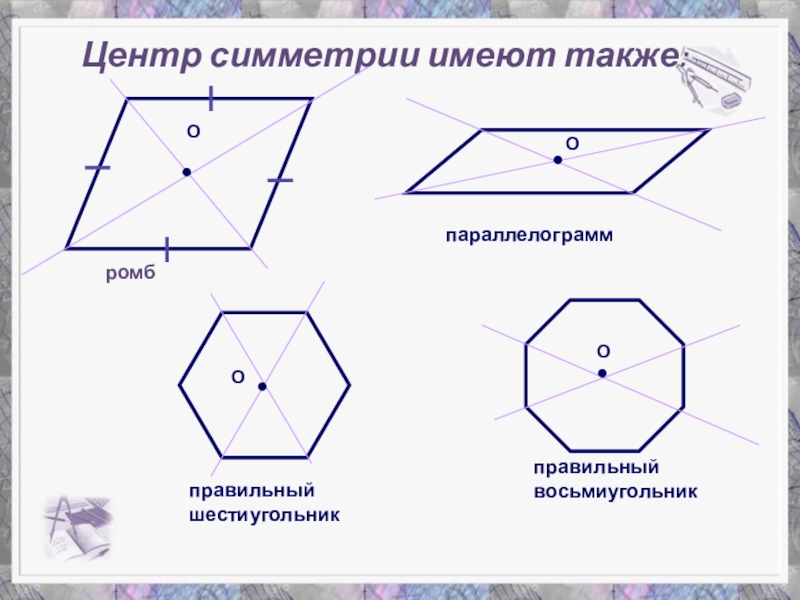
Слайд 23Центр симметрии имеют также:
ромб
параллелограмм
правильный шестиугольник
правильный
восьмиугольник
●
●
●
●
О
О
О
О
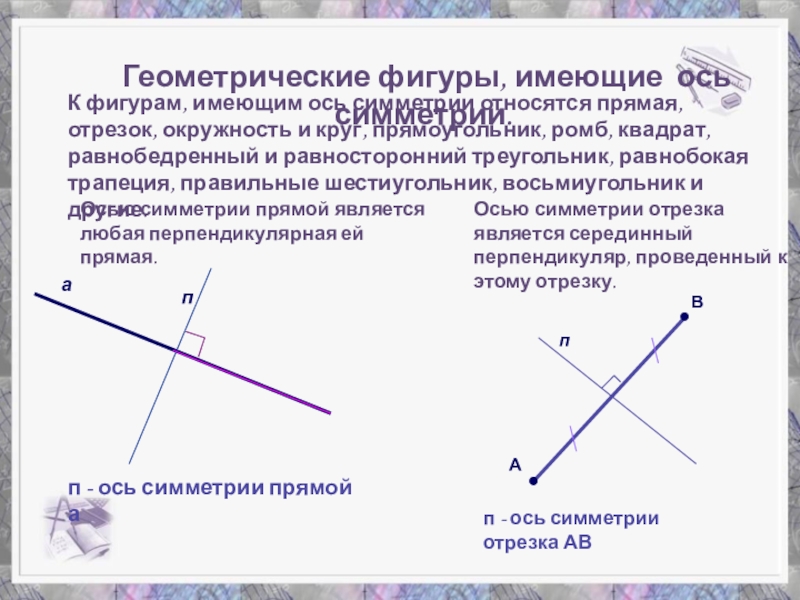
Слайд 24 Геометрические фигуры, имеющие ось симметрии.
К фигурам, имеющим ось симметрии относятся
прямая, отрезок, окружность и круг, прямоугольник, ромб, квадрат, равнобедренный и равносторонний треугольник, равнобокая трапеция, правильные шестиугольник, восьмиугольник и другие.
Осью симметрии прямой является любая перпендикулярная ей прямая.
а
п
Осью симметрии отрезка является серединный перпендикуляр, проведенный к этому отрезку.
А
В
●
●
п
п - ось симметрии прямой а
п - ось симметрии отрезка АВ
Слайд 25Ось симметрии окружности (или круга) – прямая, проходящая через центр окружности
(круга).
●
О
Оси симметрии прямоугольника – прямые, проходящие через середины противолежащих сторон.
Оси симметрии квадрата –прямые, проходящие через середины его сторон и прямые, содержащие диагонали.
О
О
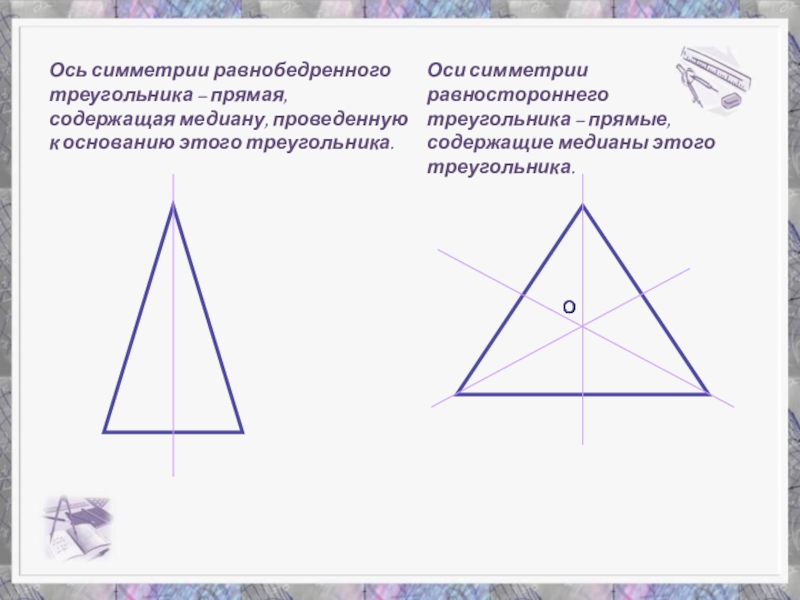
Слайд 26Ось симметрии равнобедренного треугольника – прямая, содержащая медиану, проведенную к основанию
этого треугольника.
Оси симметрии равностороннего треугольника – прямые, содержащие медианы этого треугольника.
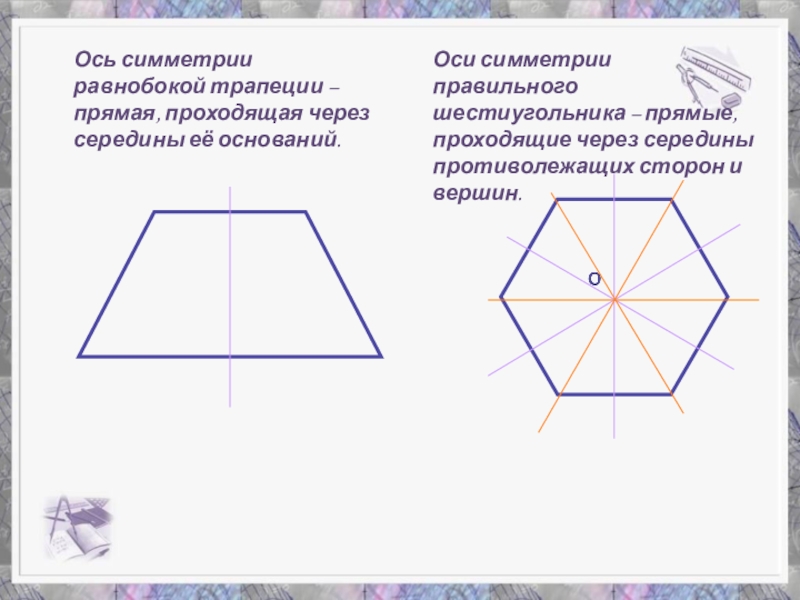
Слайд 27Ось симметрии равнобокой трапеции – прямая, проходящая через середины её оснований.
Оси
симметрии правильного шестиугольника – прямые, проходящие через середины противолежащих сторон и вершин.
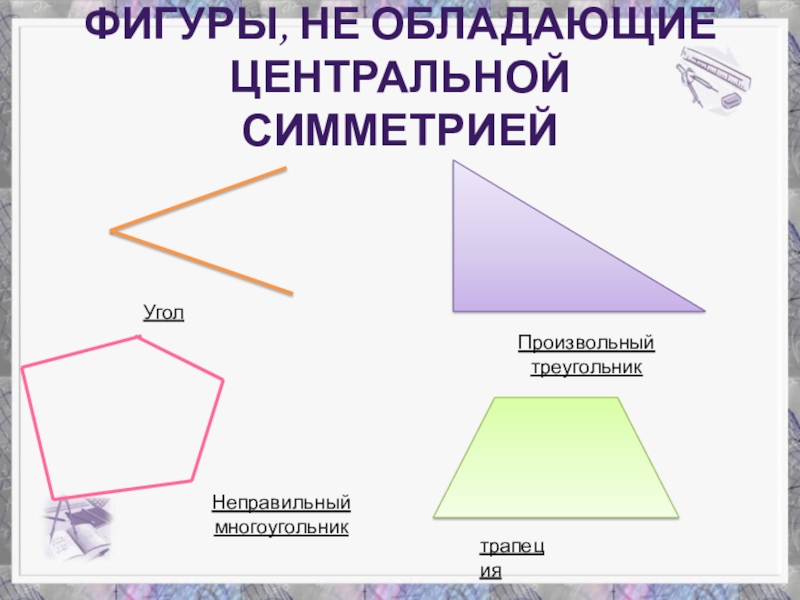
Слайд 28Фигуры, не обладающие центральной симметрией
Неправильный многоугольник
Произвольный треугольник
Угол
трапеция
Слайд 29Примеры вышеупомянутых видов симметрии .
Шар ( сфера ) обладает и центральной, и зеркальной, и
симметрией вращения. Центром симметрии является центр шара; плоскостью симметрии является плоскость любого большого круга; осью симметрии – диаметр шара.
Круглый конус обладает осевой симметрией; ось симметрии – ось конуса.
Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна её основаниям и расположена на одинаковом расстоянии между ними.
Круглый конус обладает осевой симметрией; ось симметрии – ось конуса.
Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна её основаниям и расположена на одинаковом расстоянии между ними.
Слайд 30ВЕЛИКИЕ О СИММЕТРИИ…
Термин «симметрия» придумал скульптор Пифагор Регийский.
Древние греки полагали, что
Вселенная симметрична просто потому, что она прекрасна.
Первую научную школу в истории человечества создал Пифагор Самосский.
«Симметрия – это некая «средняя мера», - считал Аристотель .
Римский врач Гален (2 в. н. э.) под симметрией понимал покой души и уравновешенность.
Первую научную школу в истории человечества создал Пифагор Самосский.
«Симметрия – это некая «средняя мера», - считал Аристотель .
Римский врач Гален (2 в. н. э.) под симметрией понимал покой души и уравновешенность.
Слайд 31Леонардо да Винчи считал, что главную роль в картине играют пропорциональность
и гармония, под которыми он понимал симметрию.
Альбрехт Дюрер (1471-1528 г.) утверждал, что каждый художник должен знать способы построения правильных симметричных фигур.
Альбрехт Дюрер (1471-1528 г.) утверждал, что каждый художник должен знать способы построения правильных симметричных фигур.
Леонардо да Винчи
Альбрехт Дюрер
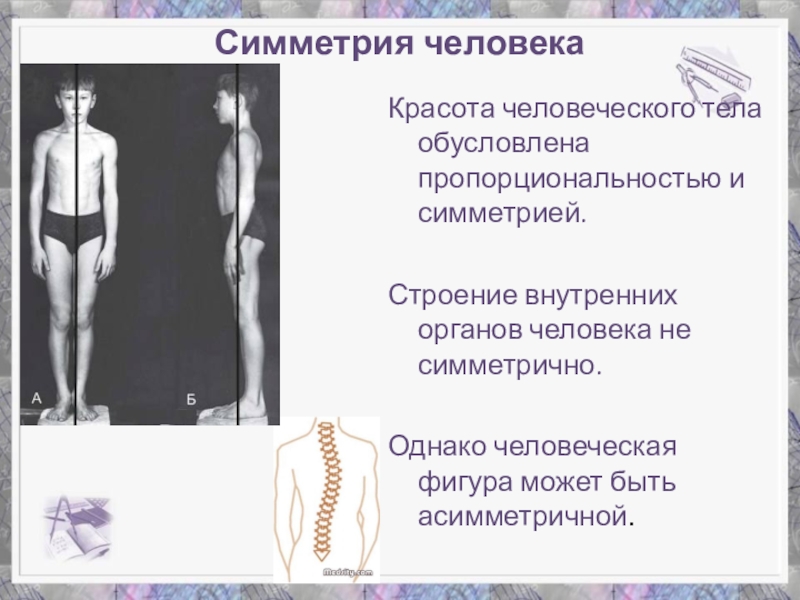
Слайд 32Симметрия человека
Красота человеческого тела обусловлена пропорциональностью и симметрией.
Строение внутренних органов
человека не симметрично.
Однако человеческая фигура может быть асимметричной.
Однако человеческая фигура может быть асимметричной.
Слайд 33Симметрия в природе
Симметрия в нашем представлении тесно связана с понятием красоты
Представления о красоте и совершенстве родились и упрочились под воздействием окружающей природы еще у наших далеких предков.. Особенно поражали кристаллы правильностью своих пропорций, безукоризненным повторением формы.
Слайд 34Каждая снежинка – это маленький кристалл замерзшей воды. Форма снежинок может
быть очень разнообразной, но все они обладают симметрией.
Все твердые тела состоят из кристаллов
Все твердые тела состоят из кристаллов
Кристаллы алмаза
Кристаллы каменной соли, кварца, арагонита
Слайд 35СИММЕТРИЯ В РАСТЕНИЯХ.
Внимательное наблюдение показывает, что основу красоты многих форм, созданных
природой, составляет симметрия.
Ярко выраженной симметрией обладают листья, ветви, цветы, плоды.
Зеркальная симметрия характерна для листьев, но встречается и у цветов.
Для цветов характерна поворотная симметрия.
Ярко выраженной симметрией обладают листья, ветви, цветы, плоды.
Зеркальная симметрия характерна для листьев, но встречается и у цветов.
Для цветов характерна поворотная симметрия.
Слайд 37СИММЕТРИЯ В ЖИВОТНОМ МИРЕ.
Симметрия встречается и в животном мире. Однако в
отличие от мира растений симметрия в животном мире наблюдается не так часто.
Рассмотрим, например, бабочку и паука.
Рассмотрим, например, бабочку и паука.
Слайд 39СИММЕТРИЯ В АРХИТЕКТУРЕ.
Нагляднее всего видна симметрия в архитектуре.
Особенно
блистательно использовали симметрию в архитектурных сооружениях древние зодчие.
В сознании древнегреческих архитекторов симметрия стала олицетворением закономерности, целесообразности, красоты.
В сознании древнегреческих архитекторов симметрия стала олицетворением закономерности, целесообразности, красоты.
Слайд 41Пирамида Хеопса Египет
Собор Парижской Богоматери Франция
Тадж Махал Турция
Биг Бэн Великобритания
Эйфелева Башня
Слайд 42Симметрия в архитектуре России
Казанский собор
Зимний Дворец
Останкинская башня
Кремль
Разводной мост
Исаакиевский Собор
Слайд 45Центральная симметрия в транспорте:
Вид сверху и вид спереди различных видов транспорта
обладает либо центральной, либо осевой симметрией.
Для наземного вида транспорта в большей степени характерна осевая симметрия. Причиной этого является направление его движения.
Центральная симметрия чаще встречается в форме воздушного и подводного транспорта, для которого направления: вправо, влево, вперед, назад, – равноценны.
Модели транспорта будущего в той же степени, что и модели настоящего и прошлого обладают различными видами.
Для наземного вида транспорта в большей степени характерна осевая симметрия. Причиной этого является направление его движения.
Центральная симметрия чаще встречается в форме воздушного и подводного транспорта, для которого направления: вправо, влево, вперед, назад, – равноценны.
Модели транспорта будущего в той же степени, что и модели настоящего и прошлого обладают различными видами.
Слайд 47СИММЕТРИЯ В ЛИТЕРАТУРЕ
В литературных произведениях существует симметрия образов, положений, мышления.
В греческой трагедии - виновный становится жертвой такого же преступления.
В «Евгении Онегине» А. С. Пушкина мы наблюдаем симметрию положений: «Онегин, отвергнувший когда-то любовь Татьяны, сам через несколько лет вынужден испытывать горечь отвергнутой любви».
В «Евгении Онегине» А. С. Пушкина мы наблюдаем симметрию положений: «Онегин, отвергнувший когда-то любовь Татьяны, сам через несколько лет вынужден испытывать горечь отвергнутой любви».
Слайд 48СИММЕТРИЯ В РУССКОМ
ЯЗЫКЕ.
Буквы русского языка тоже можно рассмотреть с
точки зрения симметрии.
Вертикальная ось симметрии: А; Д; Л; М; П; Т;Ф; Ш.
Горизонтальная ось симметрии: В; Е; З; К; С; Э; Ю.
И вертикальные, и горизонтальные оси симметрии: Ж; Н; О; Х.
Ни вертикальные, ни горизонтальные оси: Б; Г;И; Й; Р; У; Ц; Ч; Щ; Я.
Вертикальная ось симметрии: А; Д; Л; М; П; Т;Ф; Ш.
Горизонтальная ось симметрии: В; Е; З; К; С; Э; Ю.
И вертикальные, и горизонтальные оси симметрии: Ж; Н; О; Х.
Ни вертикальные, ни горизонтальные оси: Б; Г;И; Й; Р; У; Ц; Ч; Щ; Я.
Слайд 49В русском языке есть «симметричные слова – палиндромы, которые можно читать
одинаково в двух направлениях:
Шалаш, казак, радар, Алла, Анна, кок, поп.
Могут быть палиндромическими и предложения.
А роза упала на лапу Азора.
Я иду с мечём судия.
Г.Р. Державин.
Шалаш, казак, радар, Алла, Анна, кок, поп.
Могут быть палиндромическими и предложения.
А роза упала на лапу Азора.
Я иду с мечём судия.
Г.Р. Державин.
Слайд 50СИММЕТРИЯ В ОРНАМЕНТАХ
Принцип симметрия используется в построении орнамента.
Орнамент – узор, состоящий
из повторяющихся, ритмически упорядоченных элементов.
Слайд 52Оказывается, что без симметрии наш мир выглядел бы совсем по-другому. Ведь
это именно на симметрии основаны многие законы сохранения. Например, законы сохранения энергии, импульса и момента импульса являются следствиями пространственно-временных симметрий, которые являются, как математическими, так и физическими симметриями. И без этих симметрий не было бы законов сохранений, которые во многом управляют нашим миром.
Так что симметрия – пожалуй, чуть ли не самая главная вещь во Вселенной.
Так что симметрия – пожалуй, чуть ли не самая главная вещь во Вселенной.
