- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему векторы
Содержание
- 1. векторы
- 2. Понятие вектораОтрезок, для которого указано, какая его
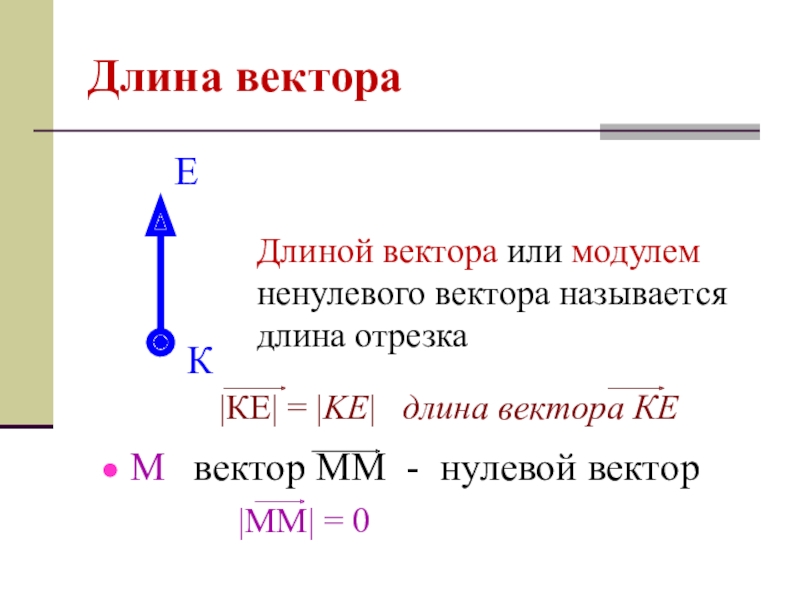
- 3. Длина вектораДлиной вектора или модулем ненулевого вектора называется длина отрезка
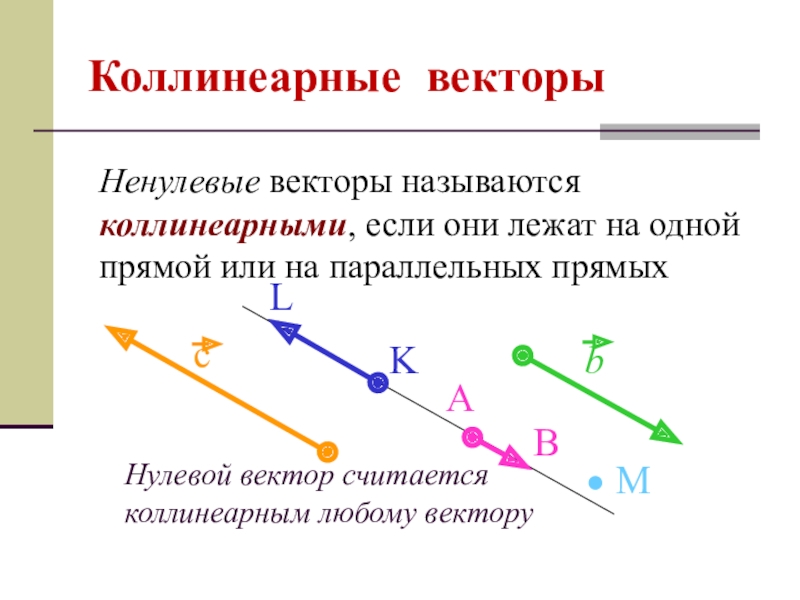
- 4. Нулевой вектор считается коллинеарным любому векторуКоллинеарные векторыНенулевые
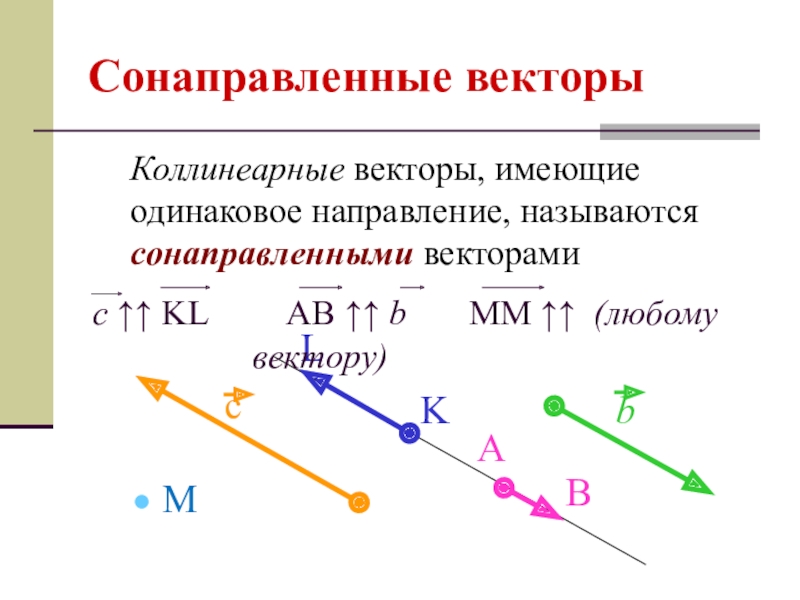
- 5. Сонаправленные векторыКоллинеарные векторы, имеющие одинаковое направление, называются сонаправленными векторами
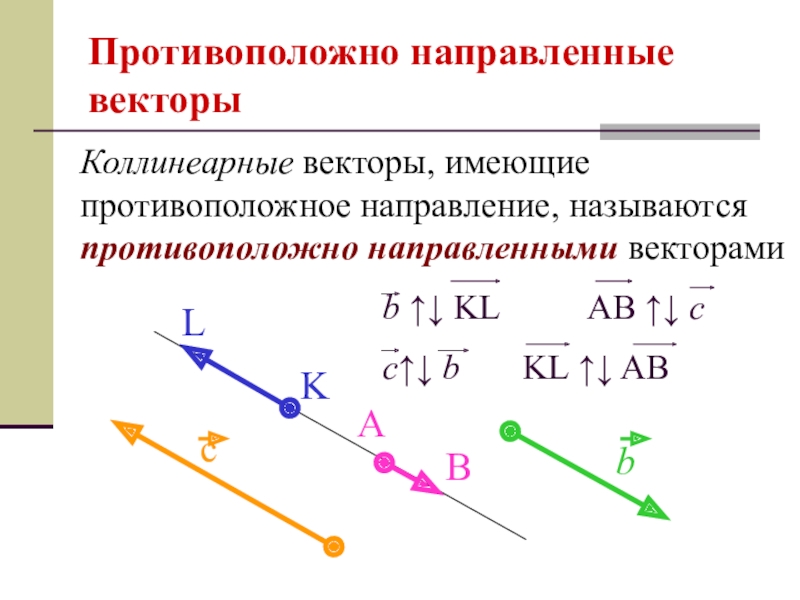
- 6. Противоположно направленные векторыКоллинеарные векторы, имеющие противоположное направление, называются противоположно направленными векторами
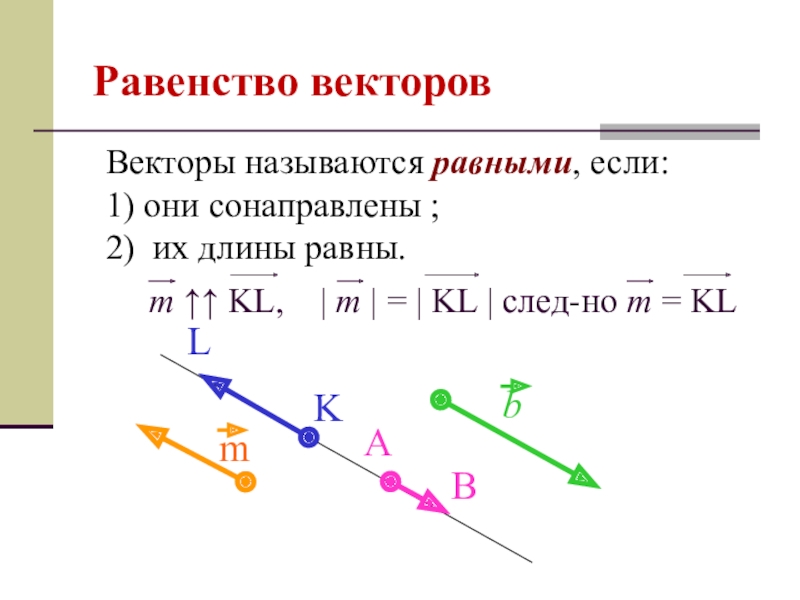
- 7. Равенство векторовВекторы называются равными, если: 1) они сонаправлены ;2) их длины равны.m
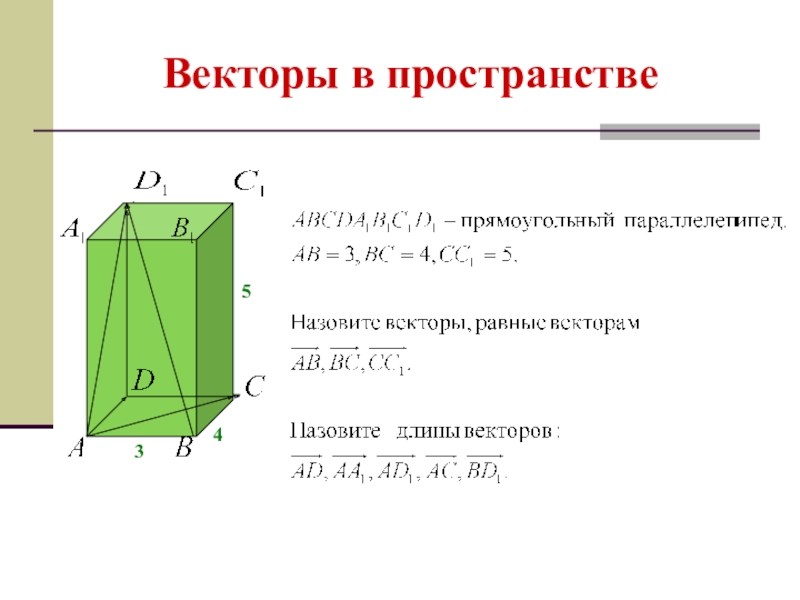
- 8. Векторы в пространстве
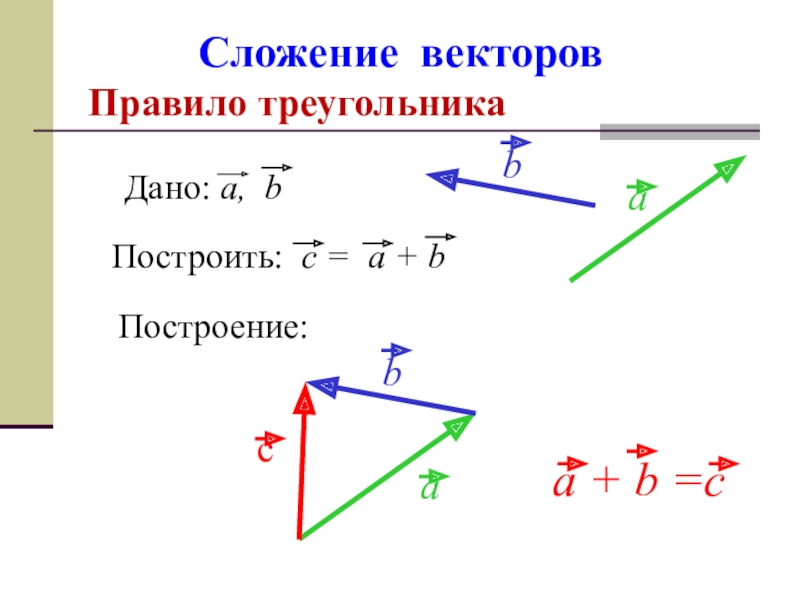
- 9. Сложение векторов Правило треугольникаПостроение:
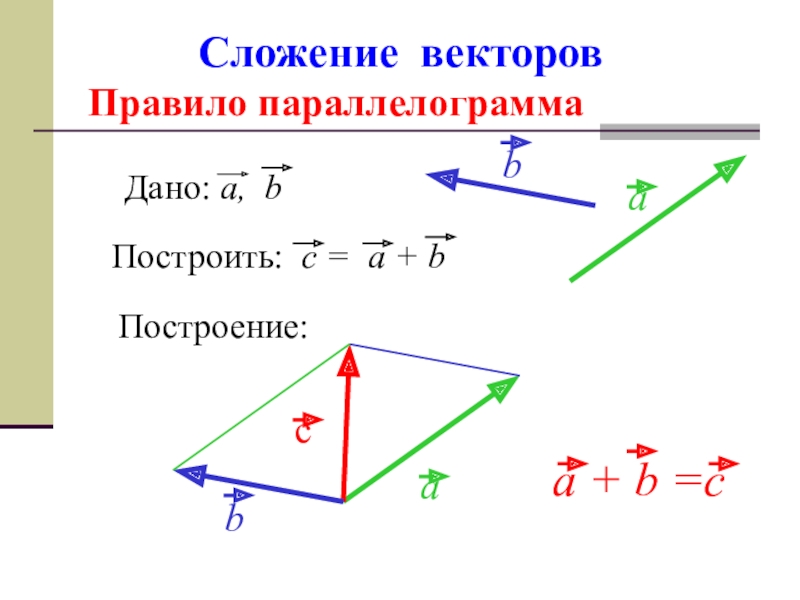
- 10. Сложение векторов Правило параллелограммаПостроение:
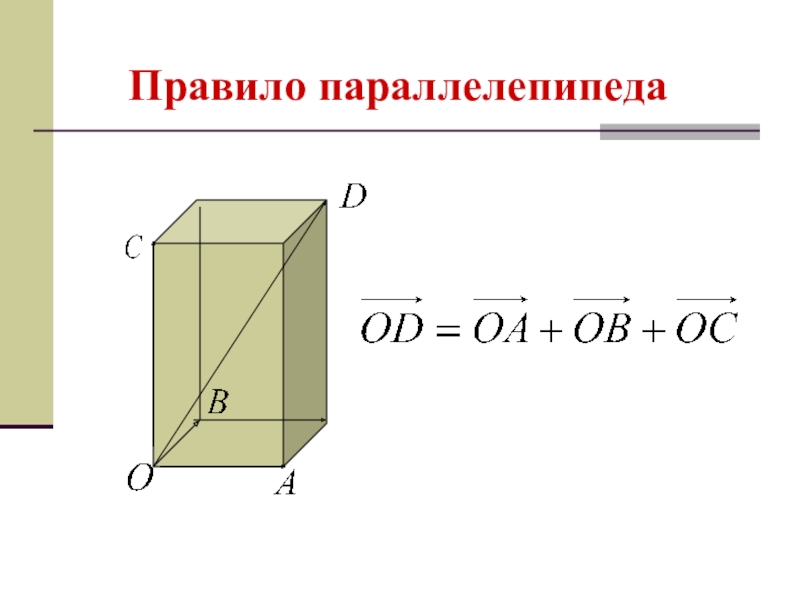
- 11. Правило параллелепипеда
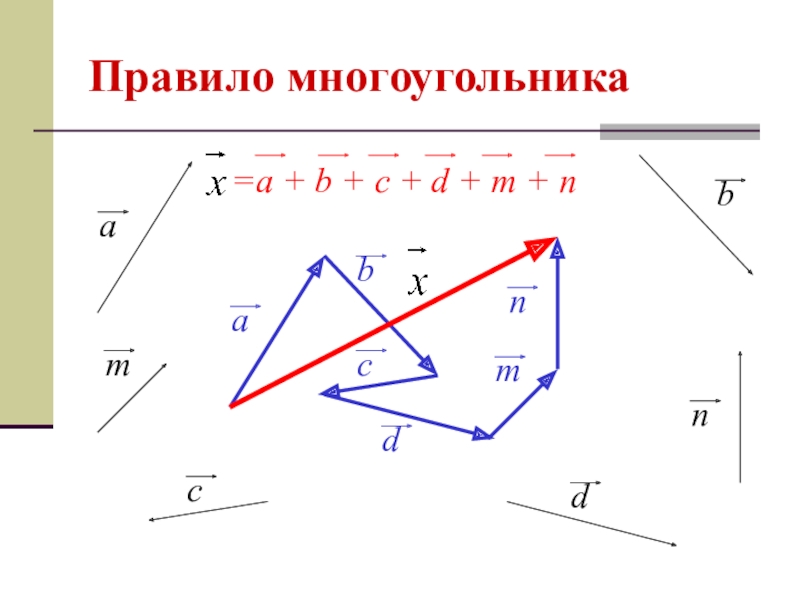
- 12. Правило многоугольника
- 13. Вычитание векторовПостроение:
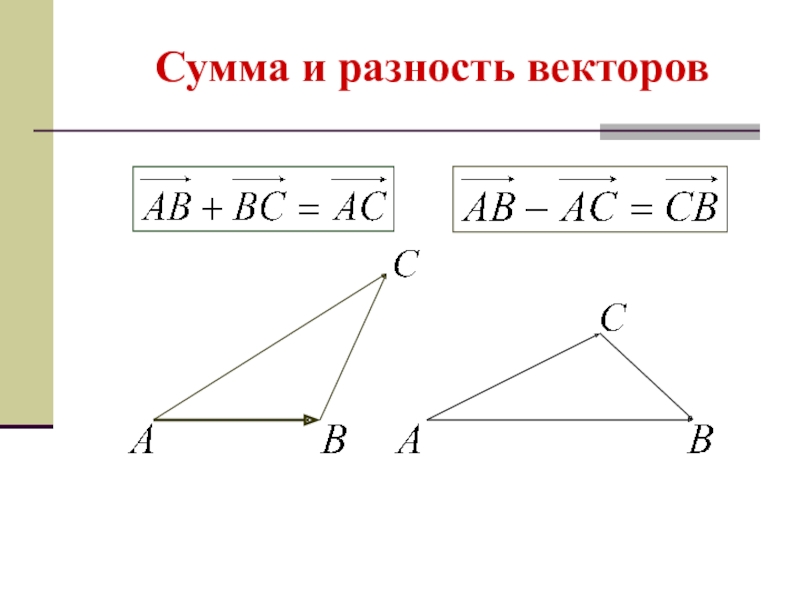
- 14. Сумма и разность векторов
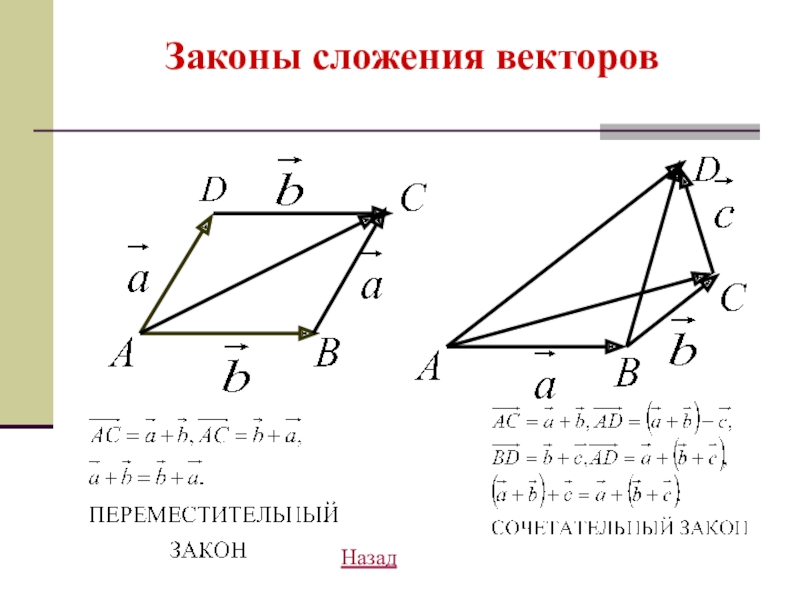
- 15. Законы сложения векторовНазад
- 16. Умножение вектора a на число kk·a =
- 17. Умножение вектора на число
- 18. Умножение вектора на число
- 19. Умножение вектора на число
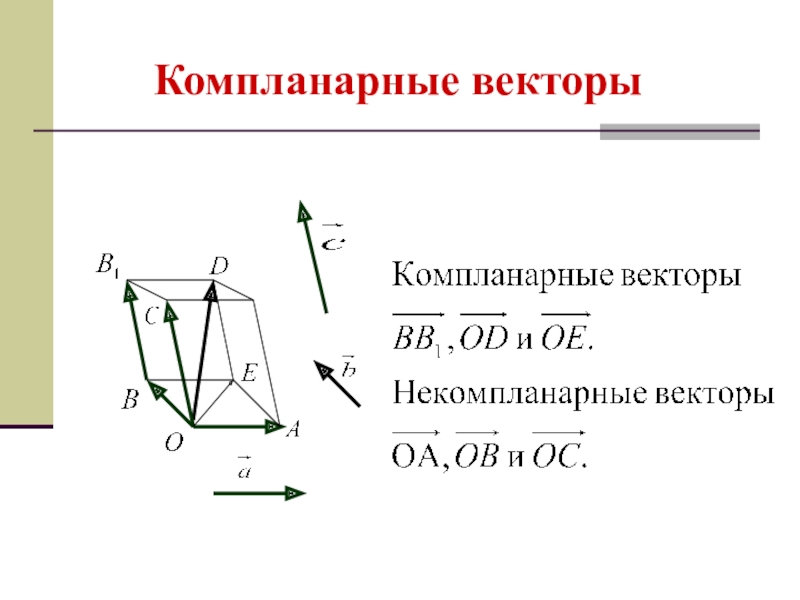
- 20. Компланарные векторыВекторы называются компланарными, если при откладывании
- 21. Компланарные векторы
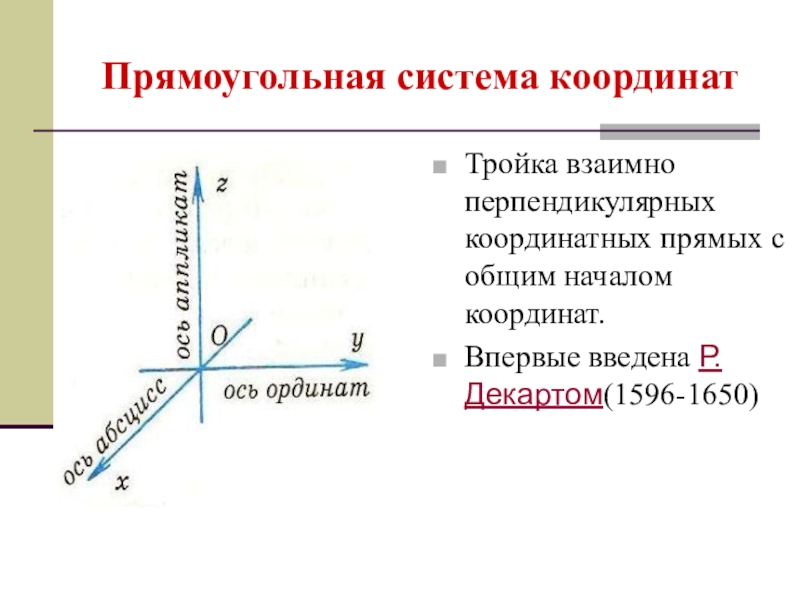
- 22. Прямоугольная система координатТройка взаимно перпендикулярных координатных прямых с общим началом координат.Впервые введена Р.Декартом(1596-1650)
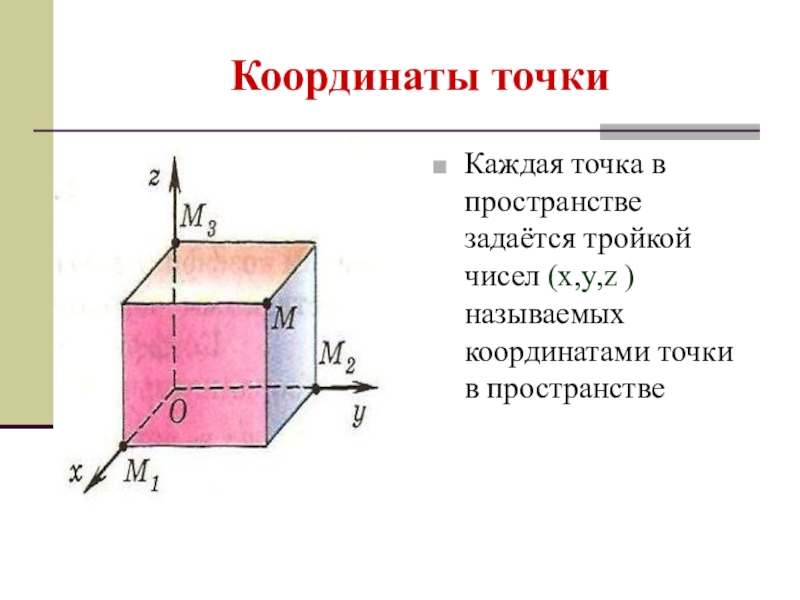
- 23. Координаты точкиКаждая точка в пространстве задаётся тройкой чисел (x,y,z ) называемых координатами точки в пространстве
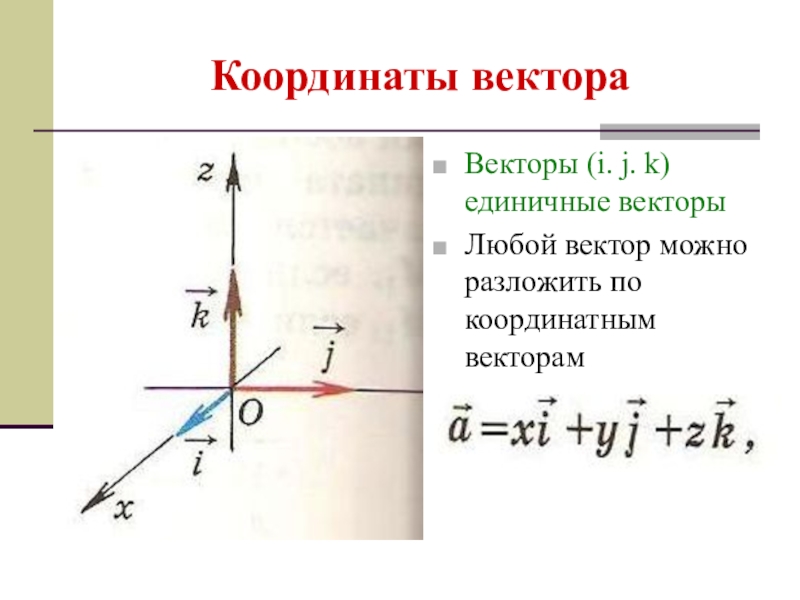
- 24. Координаты вектораВекторы (i. j. k) единичные векторыЛюбой вектор можно разложить по координатным векторам
- 25. Длина вектора
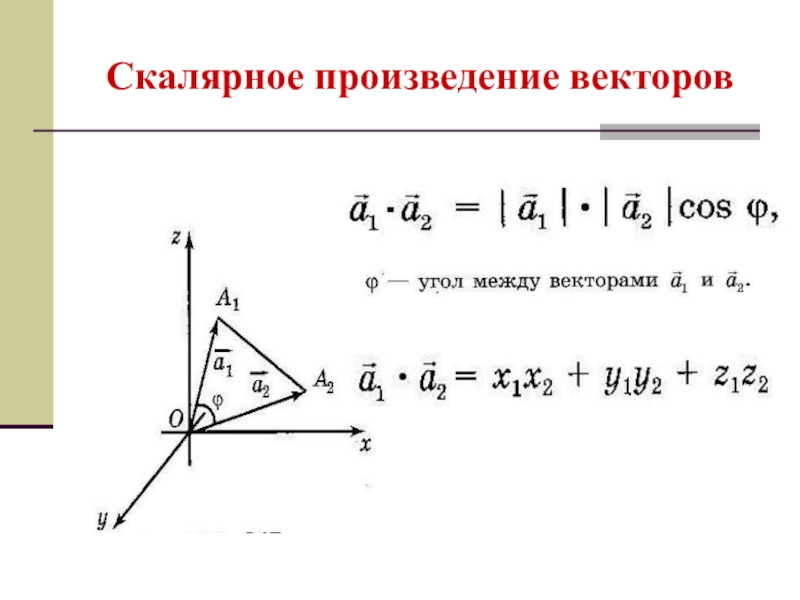
- 26. Скалярное произведение векторов
- 27. Свойства скалярного произведения. Угол между векторами.
Понятие вектораОтрезок, для которого указано, какая его граничная точка является началом, а какая - концом, называется направленным отрезком или векторомКонец вектораНачало вектора либо а a
Слайд 2Понятие вектора
Отрезок, для которого указано, какая его граничная точка является началом,
а какая - концом, называется направленным отрезком или вектором
Конец вектора
Начало вектора
либо а
a
Слайд 4Нулевой вектор считается коллинеарным любому вектору
Коллинеарные векторы
Ненулевые векторы называются коллинеарными, если
они лежат на одной прямой или на параллельных прямых
Слайд 5Сонаправленные векторы
Коллинеарные векторы, имеющие одинаковое направление, называются сонаправленными векторами
Слайд 6Противоположно направленные векторы
Коллинеарные векторы, имеющие противоположное направление, называются противоположно направленными векторами
Слайд 16Умножение вектора a на число k
k·a = b,
|a| ≠ 0, k
– произвольное число
|b| = |k|·|a|,
если k> 0, то a ↑↑ b
если k< 0, то a ↑↓ b
|b| = |k|·|a|,
если k> 0, то a ↑↑ b
если k< 0, то a ↑↓ b
Слайд 20Компланарные векторы
Векторы называются компланарными,
если при откладывании их от одной точки
они будут
лежать в одной плоскости.
лежать в одной плоскости.
Если хотя бы один из трёх векторов — нулевой, то три вектора считаются компланарными.
Тройка векторов, содержащая пару коллинеарных векторов, компланарна.
Замечания
Слайд 22Прямоугольная система координат
Тройка взаимно перпендикулярных координатных прямых с общим началом координат.
Впервые
введена Р.Декартом(1596-1650)
Слайд 23Координаты точки
Каждая точка в пространстве задаётся тройкой чисел (x,y,z ) называемых
координатами точки в пространстве
Слайд 24Координаты вектора
Векторы (i. j. k) единичные векторы
Любой вектор можно разложить по
координатным векторам