- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок Решение стереометрических задач
Содержание
- 1. Урок Решение стереометрических задач
- 2. Что нужно знать?Стереометрическая задача - несложное задание
- 3. Повторим теориюКвадрат гипотенузы равен сумме квадратов катетов.Квадрат
- 4. Формулы площадей и объемов фигур
- 5. Найдите высоту правильной треугольной пирамиды, стороны основания
- 6. Объем параллелепипеда равен 9. Найдите объем треугольной
- 7. Площадь боковой поверхности цилиндра равна 56π, а
- 8. Диаметр основания конуса равен 42, а длина
- 9. Задача 1В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
- 10. Задача 5В правильной четырехугольной пирамиде SABCD точка
- 11. Успехов на ЕГЭ!
Слайд 1Решение стереометрических задач
ученица 11 класса
Воеводина Н.
Учитель:
Приймак Э.И.
Слайд 2Что нужно знать?
Стереометрическая задача - несложное задание на вычисление элементов, площадей
Для решения задач необходимо знать:
1. Теорему Пифагора.
2. Теорему косинусов.
3. Определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике.
4. Формулы площадей фигур (треугольник, прямоугольник, параллелограмм, круг, трапеция).
5. Формулы объёмов тел.
6. Свойства правильных пирамид и призм.
Слайд 3Повторим теорию
Квадрат гипотенузы равен сумме квадратов катетов.
Квадрат стороны треугольника равен сумме
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе. Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему.
Свойства правильной призмы
1. Основания правильной призмы являются правильными многоугольниками.
2. Боковые грани правильной призмы являются равными прямоугольниками.
3. Боковые ребра правильной призмы равны.
Свойства правильной пирамиды
1. Основание правильной пирамиды — правильный многоугольник. 2. Боковые грани правильной пирамиды — равнобедренные треугольники. 3. Боковые ребра правильной пирамиды равны.
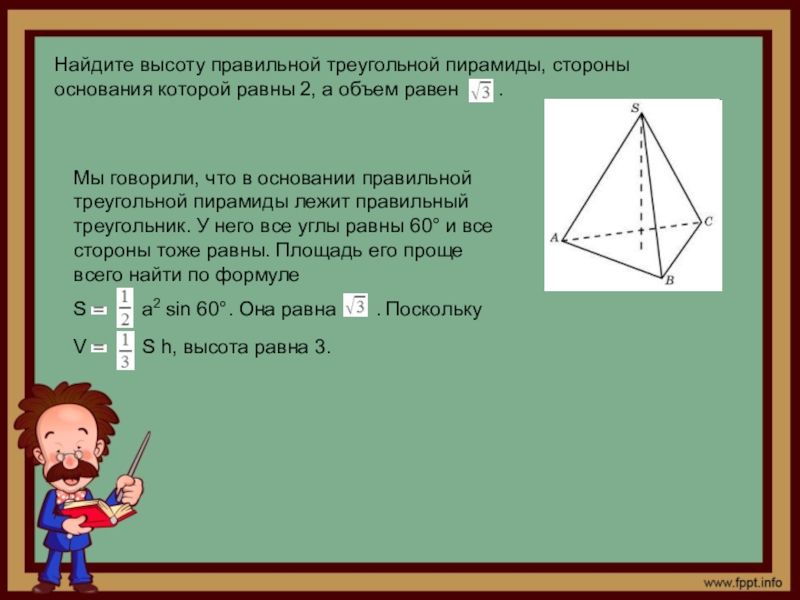
Слайд 5Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен
Мы говорили, что в основании правильной треугольной пирамиды лежит правильный треугольник. У него все углы равны 60° и все стороны тоже равны. Площадь его проще всего найти по формуле
S a2 sin 60°. Она равна . Поскольку V S h, высота равна 3.
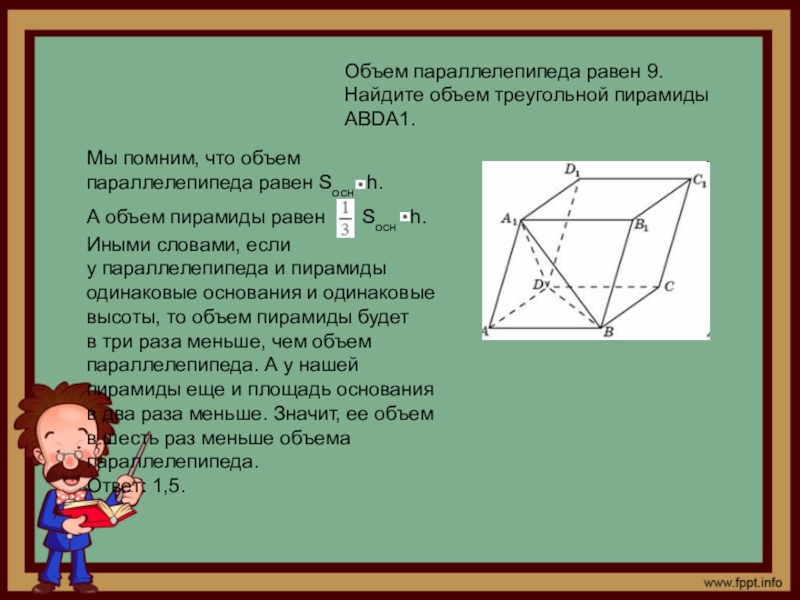
Слайд 6Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды АВDА1.
Мы помним, что
Ответ: 1,5.
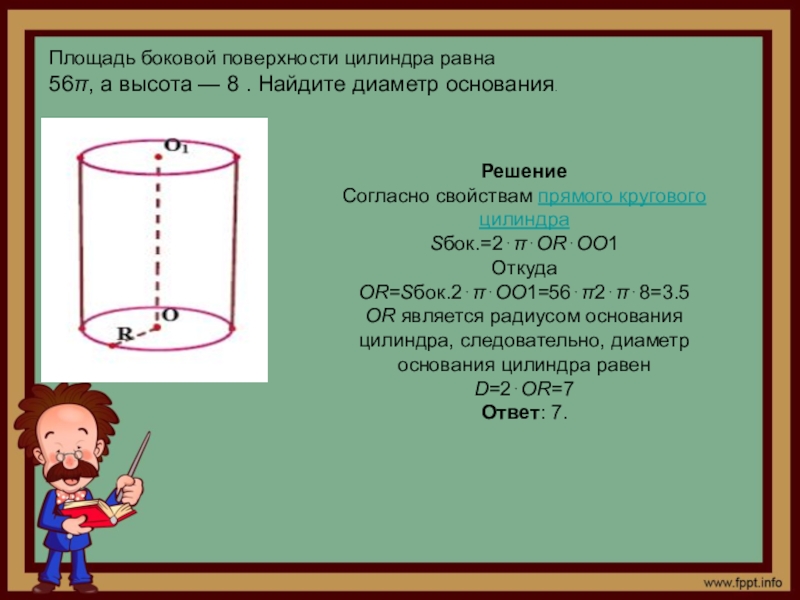
Слайд 7Площадь боковой поверхности цилиндра равна
56π, а высота — 8 .
Решение
Согласно свойствам прямого кругового цилиндра
Sбок.=2⋅π⋅OR⋅OO1
Откуда
OR=Sбок.2⋅π⋅OO1=56⋅π2⋅π⋅8=3.5
OR является радиусом основания цилиндра, следовательно, диаметр основания цилиндра равен
D=2⋅OR=7
Ответ: 7.
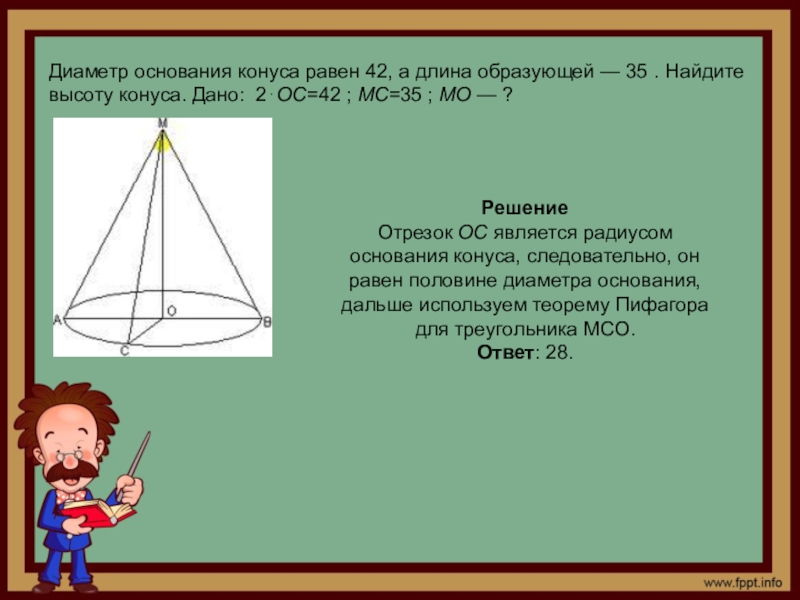
Слайд 8Диаметр основания конуса равен 42, а длина образующей — 35 .
Решение
Отрезок OC является радиусом основания конуса, следовательно, он равен половине диаметра основания,
дальше используем теорему Пифагора для треугольника МСО.
Ответ: 28.
Слайд 9Задача 1
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите
Ответ: 2
Задача 2
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны √5. Найдите расстояние между точками B и E1.
Ответ: 5
Задача 3
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.
Ответ: 60
Задача 4
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол AC1C. Ответ дайте в градусах.
Ответ: 60
Слайд 10Задача 5
В правильной четырехугольной пирамиде SABCD точка O - центр основания,
Ответ: 6
Задача 6
В правильной треугольной пирамиде SABC R - середина ребра BC, S - вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.
Ответ: 3
Задача 7
В правильной треугольной пирамиде SABC L - середина ребра BC, S - вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.
Ответ: 1
Задача 8
В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.
Ответ: 1