учитель математики
Пархоменко Н.А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок презентация по математике:Многогранники
Содержание
- 1. Урок презентация по математике:Многогранники
- 2. Параллелепипед. АВСD и A1B1C1D1 – равные параллелограммы
- 3. Прямой параллелепипед – это параллелепипед, у которого боковые грани являются прямоугольниками.АВСDA1B1С1D1abc
- 4. Прямоугольный параллелепипед – это параллелепипед, у которого
- 5. Призма- основания – равные n – угольники,
- 6. Пирамида – это многогранник, состоящий из n-угольника
- 7. Правильная пирамида основание – правильный многоугольник, вершина
- 8. PA1A2…An – произвольная пирамидаα – плоскость основанияβ
- 9. Правильные
- 10. Слайд 10
- 11. Правильный октаэдр составлен из восьми равносторонних треугольников.
- 12. Правильный икосаэдр составлен из двадцати равносторонних треугольников.
- 13. Куб (гексаэдр) составлен из шести квадратов. Каждая
- 14. Правильный додекаэдр составлен из двенадцати правильных пятиугольников.
- 15. Сечение многогранников.Секущая плоскость - плоскость, по обе
- 16. Основные виды сечений многогранников:Параллельное сечение – сечение,
- 17. Слайд 17
- 18. Задача № 219 1) Доказать, что ∆
- 19. Решение:1) ∆ BDD1-прямоуг.,т.к. DD1┴ пл. ABC (по
- 20. Задача № 2211) доказать: ∆АА1В- прямоуг.найти
- 21. Решение:∆АА1В- прямоуг.Т.к. АА1┴ пл. АВС(по усл. призма
- 22. Слайд 22
Параллелепипед. АВСD и A1B1C1D1 – равные параллелограммы – основания АА1|| ВВ1|| СС1|| DD1 – боковые ребра Все грани параллелограммы.AA1B1B; BB1C1C; CC1D1D; AA1D1D – боковые граниDB1 – диагональ Свойства.1. Противолежащие грани параллелепипеда
Слайд 1Многогранники
Геометрия 10 - 11 класс
Выполнила
Ученица 10 класса
Еременко Любовь.
Руководитель:
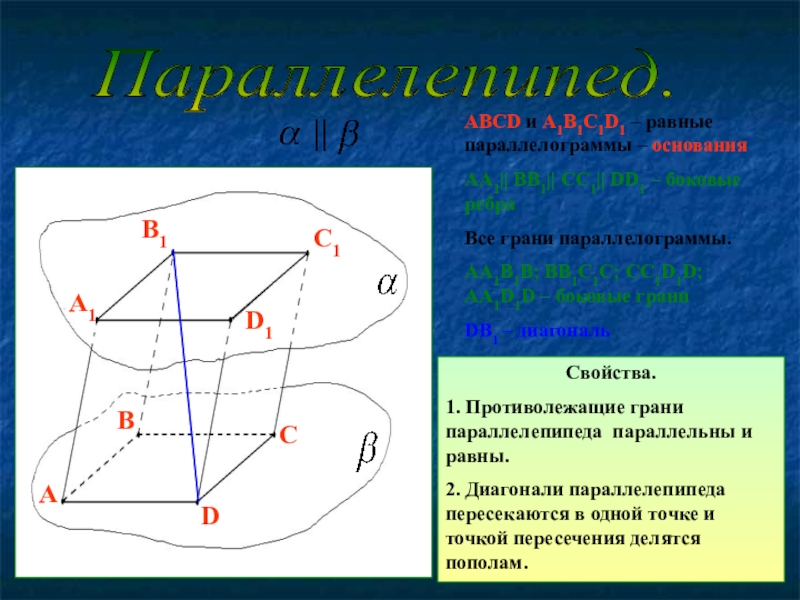
Слайд 2Параллелепипед.
АВСD и A1B1C1D1 – равные параллелограммы – основания
АА1|| ВВ1||
СС1|| DD1 – боковые ребра
Все грани параллелограммы.
AA1B1B; BB1C1C; CC1D1D; AA1D1D – боковые грани
DB1 – диагональ
Все грани параллелограммы.
AA1B1B; BB1C1C; CC1D1D; AA1D1D – боковые грани
DB1 – диагональ
Свойства.
1. Противолежащие грани параллелепипеда параллельны и равны.
2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
А
В
С
D
А1
В1
С1
D1
Слайд 3Прямой параллелепипед
– это параллелепипед, у которого боковые грани являются
прямоугольниками.
А
В
С
D
A1
B1
С1
D1
a
b
c
Слайд 4Прямоугольный параллелепипед
– это параллелепипед, у которого все грани прямоугольники.
а
b
c
a –
длина, b – ширина,
с – высота, d – диагональ
с – высота, d – диагональ
d
d2 = a2 + b2 + c2
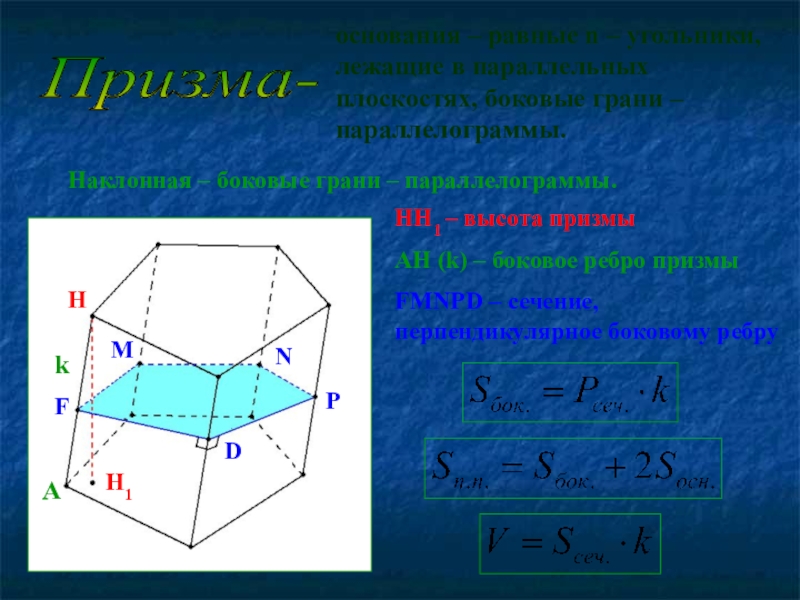
Слайд 5Призма-
основания – равные n – угольники, лежащие в параллельных плоскостях,
боковые грани – параллелограммы.
Наклонная – боковые грани – параллелограммы.
H
H1
A
k
F
M
N
P
D
HH1 – высота призмы
AH (k) – боковое ребро призмы
FMNPD – сечение, перпендикулярное боковому ребру
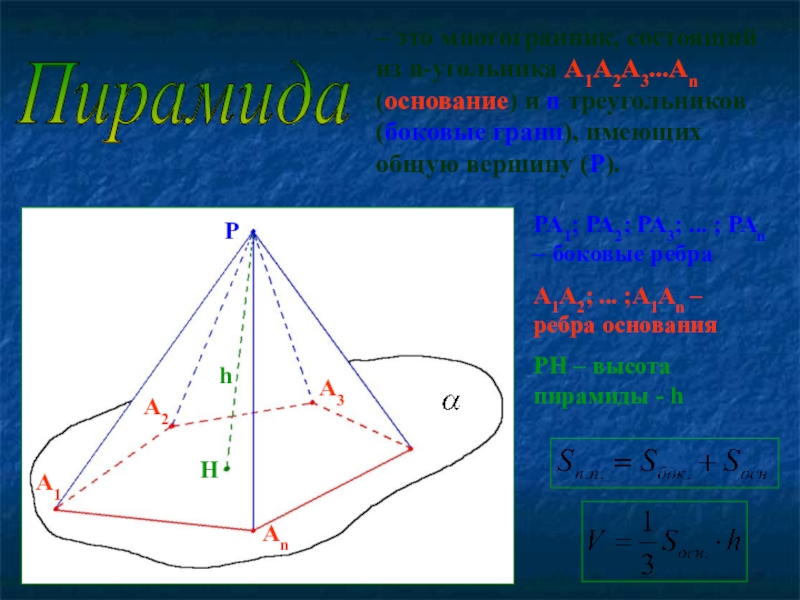
Слайд 6Пирамида
– это многогранник, состоящий из n-угольника А1А2А3...Аn (основание) и n
треугольников (боковые грани), имеющих общую вершину (Р).
Р
А1
А2
А3
Аn
H
РА1; РА2; РА3; ... ; РАn – боковые ребра
А1А2; ... ;А1Аn – ребра основания
РH – высота пирамиды - h
h
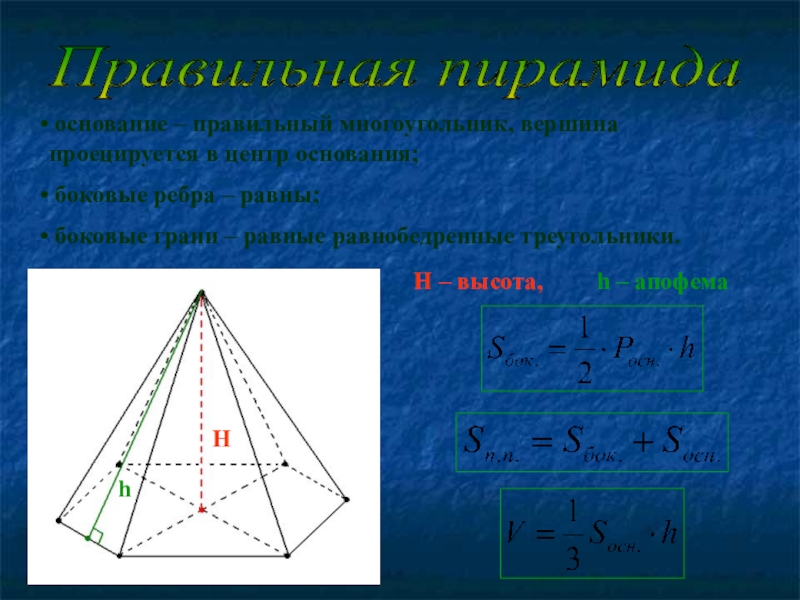
Слайд 7Правильная пирамида
основание – правильный многоугольник, вершина проецируется в центр
основания;
боковые ребра – равны;
боковые грани – равные равнобедренные треугольники.
боковые ребра – равны;
боковые грани – равные равнобедренные треугольники.
H – высота,
h – апофема
H
h
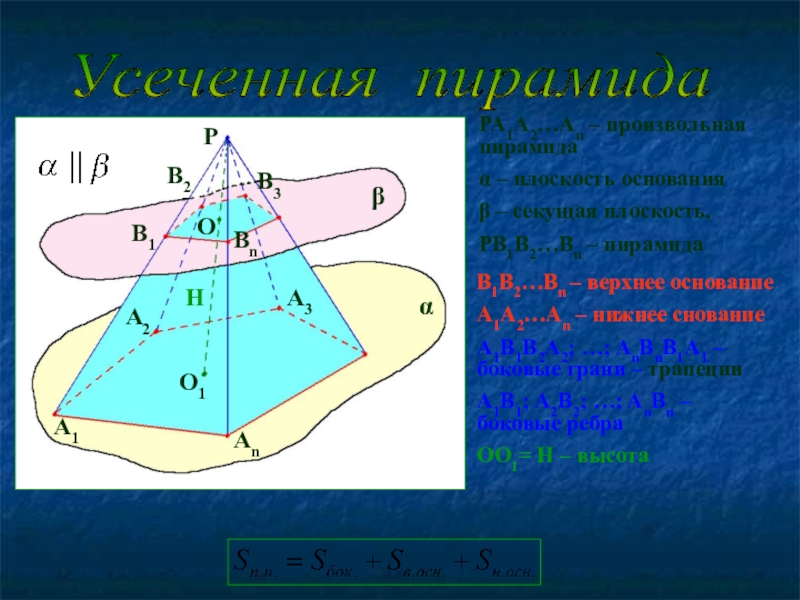
Слайд 8PA1A2…An – произвольная пирамида
α – плоскость основания
β – секущая плоскость,
PB1B2…Bn
– пирамида
Усеченная пирамида
β
α
P
A1
A2
A3
An
B1
B3
Bn
B2
O
O1
H
B1B2…Bn – верхнее основание
A1A2…An – нижнее снование
A1B1B2A2; …; AnBnB1A1 – боковые грани – трапеции
A1B1; A2B2; …; AnBn – боковые ребра
OO1= H – высота
Слайд 9 Правильные многогранники. Выпуклый многогранник называется правильным, если все его грани
- равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.
Всего существует пять видов правильных выпуклых многогранников. Их гранями являются правильные треугольники, правильные четырехугольники (квадраты) и правильные пятиугольники.
Слайд 11Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является
вершиной четырёх треугольников. Следовательно, сумма плоских углов при каждой вершине 240°
Слайд 12Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является
вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300°
Слайд 13Куб (гексаэдр) составлен из шести квадратов. Каждая вершина куба является вершиной
трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270°.
Слайд 14Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является
вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.
Слайд 15Сечение многогранников.
Секущая плоскость - плоскость, по обе стороны от которой имеются
точки данного многогранника.
Многоугольник – сторонами которого являются отрезки пересекающие грани по секущей плоскости многогранника называется сечением данного многогранника (часть секущей плоскости, заключенная внутри тела).
Слайд 16Основные виды сечений многогранников:
Параллельное сечение – сечение, плоскость которого параллельна либо
основанию, либо одной из грани многогранника.
Диагональное сечение – сечение, плоскость которого, проходит через диагонали многогранника, или диагонали оснований многогранника.
Диагональное сечение – сечение, плоскость которого, проходит через диагонали многогранника, или диагонали оснований многогранника.
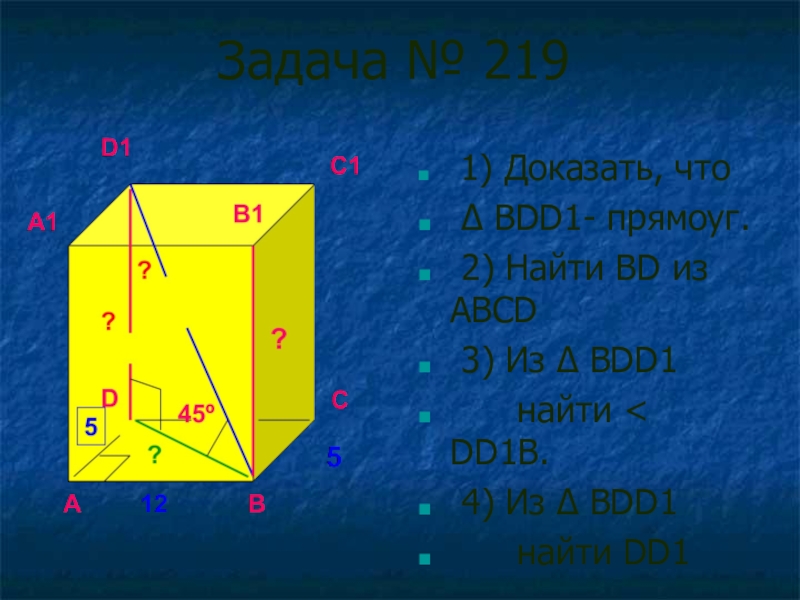
Слайд 18Задача № 219
1) Доказать, что
∆ BDD1- прямоуг.
2) Найти
BD из ABCD
3) Из ∆ BDD1
найти < DD1B.
4) Из ∆ ВDD1
найти DD1
3) Из ∆ BDD1
найти < DD1B.
4) Из ∆ ВDD1
найти DD1
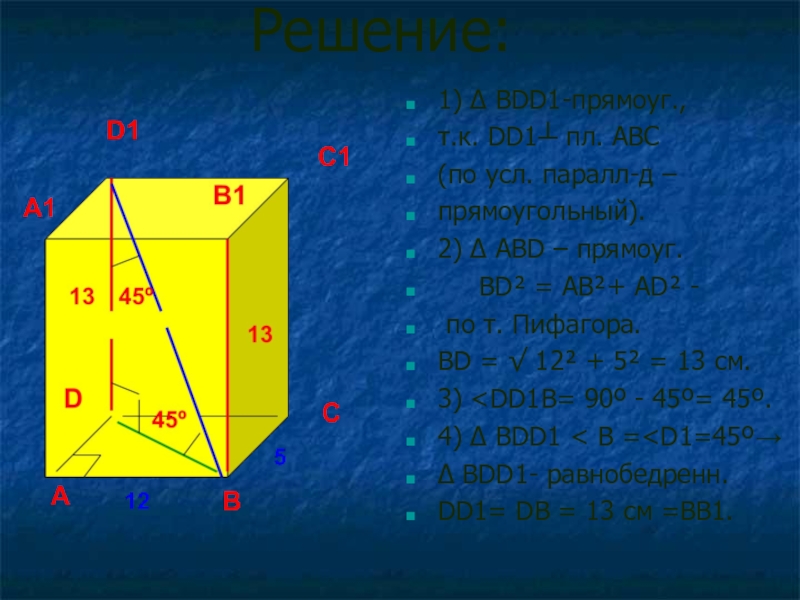
Слайд 19Решение:
1) ∆ BDD1-прямоуг.,
т.к. DD1┴ пл. ABC
(по усл. паралл-д –
прямоугольный).
2) ∆
ABD – прямоуг.
BD² = AB²+ AD² -
по т. Пифагора.
BD = √ 12² + 5² = 13 см.
3)4) ∆ BDD1 < B =∆ BDD1- равнобедренн.
DD1= DB = 13 см =ВВ1.
BD² = AB²+ AD² -
по т. Пифагора.
BD = √ 12² + 5² = 13 см.
3)
DD1= DB = 13 см =ВВ1.
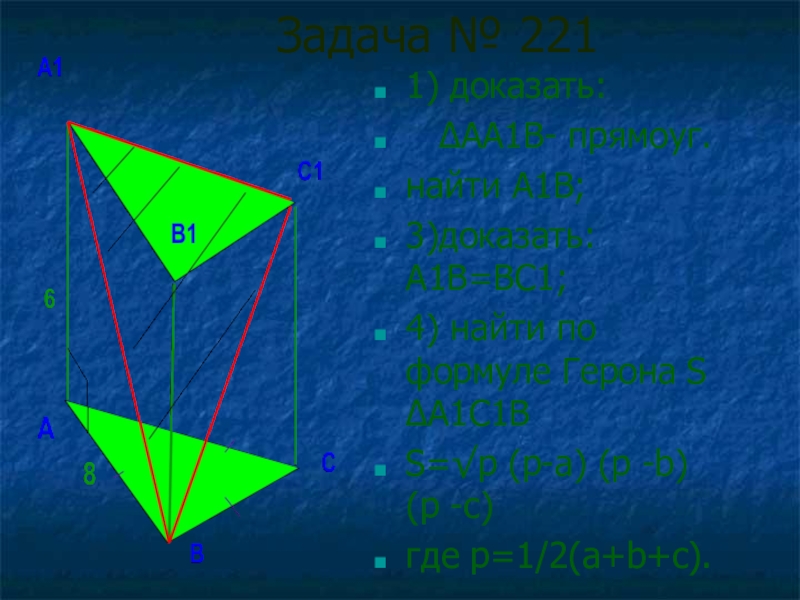
Слайд 20Задача № 221
1) доказать:
∆АА1В- прямоуг.
найти А1В;
3)доказать: А1В=ВС1;
4) найти по
формуле Герона S ∆A1C1B
S=√p (p-a) (p -b) (p -c)
где p=1/2(a+b+c).
S=√p (p-a) (p -b) (p -c)
где p=1/2(a+b+c).
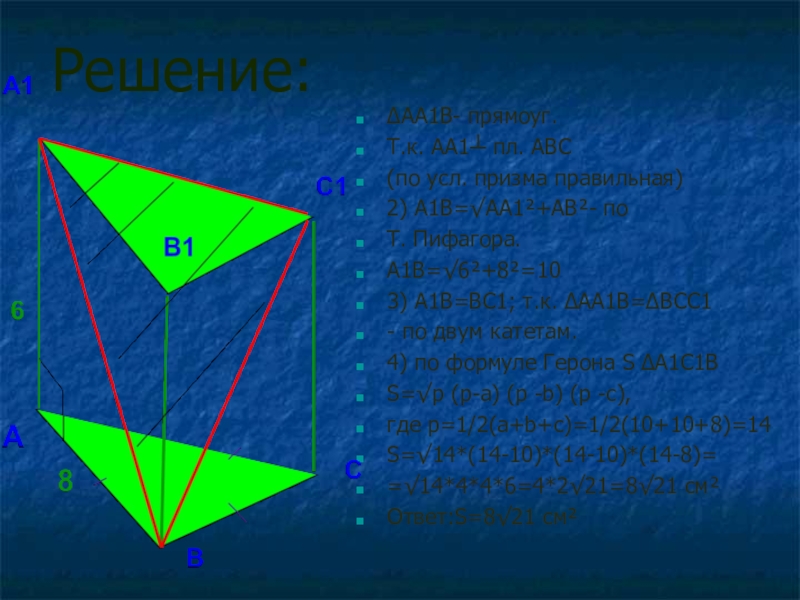
Слайд 21Решение:
∆АА1В- прямоуг.
Т.к. АА1┴ пл. АВС
(по усл. призма правильная)
2) А1В=√АА1²+АВ²- по
Т.
Пифагора.
А1В=√6²+8²=10
3) А1В=ВС1; т.к. ∆АА1В=∆ВСС1
- по двум катетам.
4) по формуле Герона S ∆A1C1B
S=√p (p-a) (p -b) (p -c),
где p=1/2(a+b+c)=1/2(10+10+8)=14
S=√14*(14-10)*(14-10)*(14-8)=
=√14*4*4*6=4*2√21=8√21 см²
Ответ:S=8√21 см²
А1В=√6²+8²=10
3) А1В=ВС1; т.к. ∆АА1В=∆ВСС1
- по двум катетам.
4) по формуле Герона S ∆A1C1B
S=√p (p-a) (p -b) (p -c),
где p=1/2(a+b+c)=1/2(10+10+8)=14
S=√14*(14-10)*(14-10)*(14-8)=
=√14*4*4*6=4*2√21=8√21 см²
Ответ:S=8√21 см²
