Т. А.
СТ. КАНЕВСКАЯ
2013 ГОД.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок + презентация по геометрии для 8 класса по теме Четырехугольники
Содержание
- 1. Урок + презентация по геометрии для 8 класса по теме Четырехугольники
- 2. МУЛЬТИМЕДИЙНАЯ ПРЕЗЕНТАЦИЯ.ПЛАН УРОКА.1.ОБЪЯВЛЕНИЕ ТЕМЫ УРОКА.2. ПРОВЕРКА ДОМАШНЕГО
- 3. ТЕМА УРОКА: ИТОГОВЫЙ УРОК ПО ТЕМЕ: «ЧЕТЫРЕХУГОЛЬНИКИ».
- 4. ХОД УРОКА.ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ.
- 5. Слайд 5
- 6. 2.ПРОВЕРКА ИЗУЧЕННОГО МАТЕРИАЛА. МЫ ЗАКОНЧИЛИ
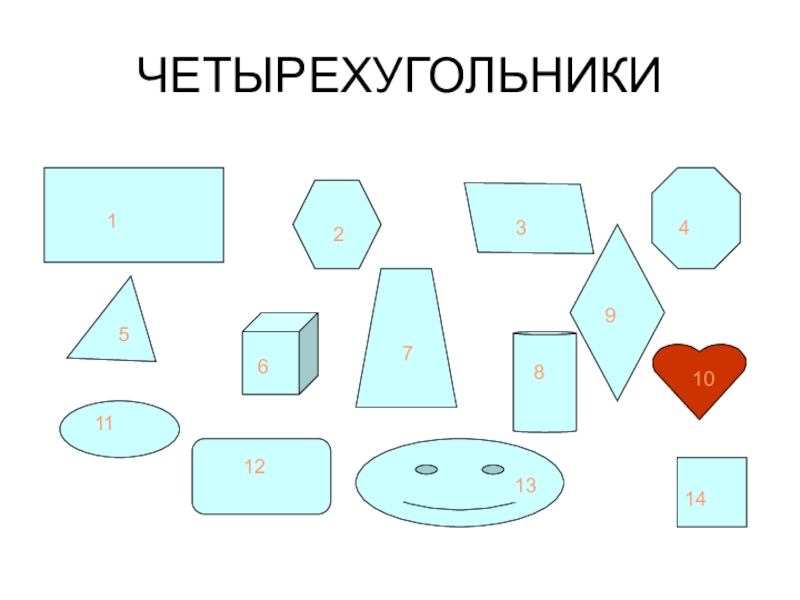
- 7. ЧЕТЫРЕХУГОЛЬНИКИ1234567891011121314
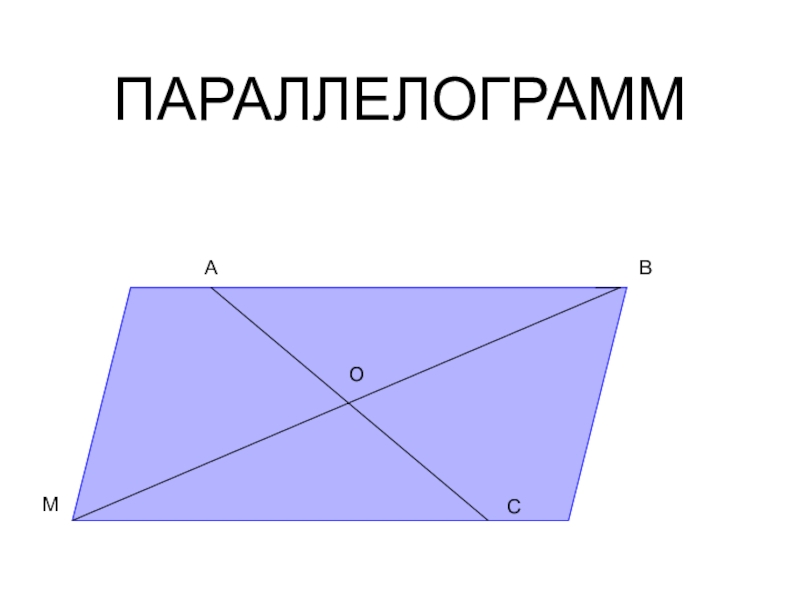
- 8. ПАРАЛЛЕЛОГРАММАВМСО
- 9. ЧТО НАЗЫВАЕТСЯ ПАРАЛЛЕЛОГРАММОМ ?ПЕРЕЧИСЛИТЬ ЕГО СВОЙСТВА.ДИАГОНАЛЬ ПАРАЛЛЕЛОГРАММА
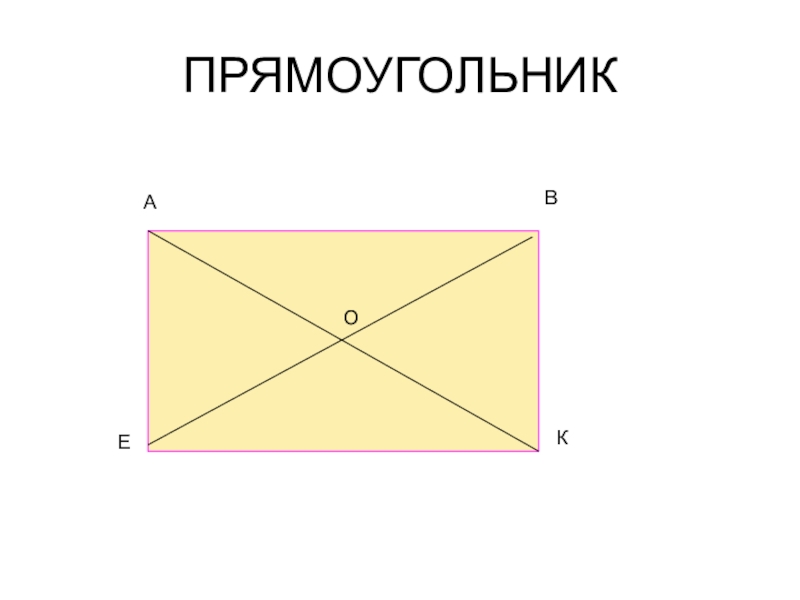
- 10. ПРЯМОУГОЛЬНИКАВЕКО
- 11. ЧТО НАЗЫВАЕТСЯ ПРЯМОУГОЛЬНИКОМ ?ПЕРЕЧИСЛИТЬ ЕГО СВОЙСТВА .ДОКАЗАТЬ, ЧТО ДИАГОНАЛИ ПРЯМОУГОЛЬ-НИКА РАВНЫ.ПРОЧИТАТЬ ПРИЗНАК ПАРАЛЛЕЛОГРАММА.
- 12. РОМБАВСМО
- 13. ЧТО НАЗЫВАЕТСЯ РОМБОМ ?ПЕРЕЧИСЛИТЬ СВОЙСТВА РОМБА.КАК ЕЩЕ МОЖНО ОПРЕДЕЛИТЬ РОМБ?
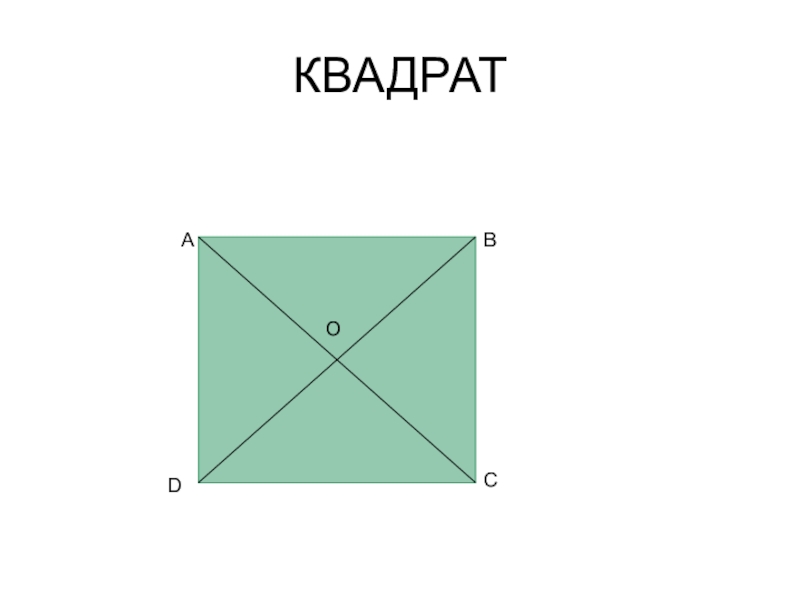
- 14. КВАДРАТАВСDО
- 15. ЧТО НАЗЫВАЕТСЯ КВАДРАТОМ?ПЕРЕЧИСЛИТ ЕГО СВОЙСТВА.КАК ЕЩЕ МОЖНО ОПРЕДЕЛИТЬ КВАДРАТ?
- 16. ТРАПЕЦИЯАВСD
- 17. ЧТО НАЗЫВАЕТСЯ ТРАПЕЦИЕЙ?КАКИЕ ВИДЫ ТРАПЕЦИЙ ВЫ ЗНАЕТЕ?КАКАЯ ТРАПЕЦИЯ НАЗЫВАЕТСЯ РАВНОБЕДРЕННОЙ?КАКИМИ СВОЙСТВАМИ ОБЛАДАЕТ РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ?
- 18. РЕШЕНИЕ ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ
- 19. ОПРЕДЕЛИТЕ ВИД ТРЕУГОЛЬНИКА АВС, ЕСЛИ АВСD – КВАДРАТ, а) по сторонам б) по угламАВСD
- 20. НАЙДИТЕ угол ВАС140ºАВСDО
- 21. ДОКАЖИТЕ, ЧТО БИССЕКТРИСА ПАРАЛЛЕЛОГРАММА ОТСЕКАЕТ ОТ НЕГО РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК.
- 22. 1122АВСДЕ
- 23. ИТАК, МЫ ДОКАЗАЛИ, ЧТО БИССЕКТРИСА УГЛА ПАРАЛЛЕЛОГРАММА
- 24. ДАНО: АВСD – ПАРАЛЛЕЛОГРАММ, АМ – БИССЕКТРИСА УГЛА А. ДОКАЗАТЬ, ЧТО ТРЕУГОЛЬНИК АВМ – РАВНОБЕДРЕННЫЙАВСD11м2
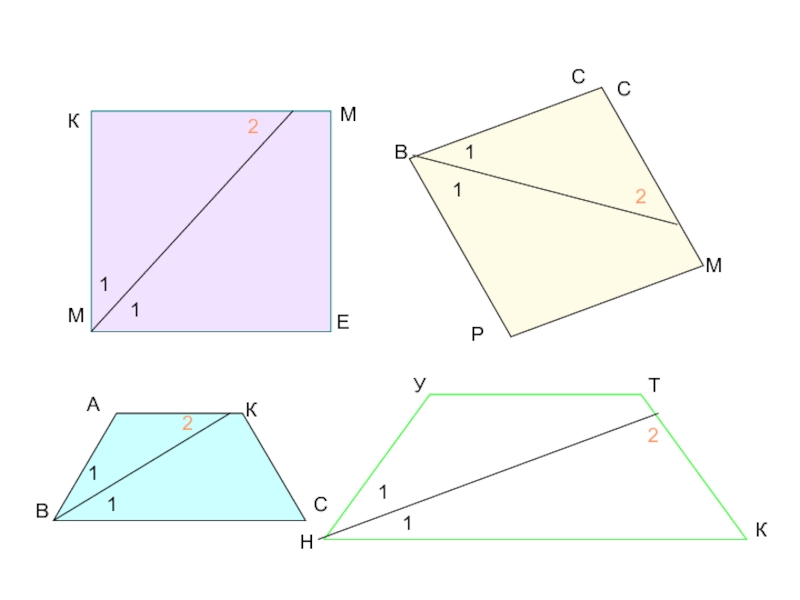
- 25. 11111111МКМЕВССМРАКСВНУТК2222
- 26. Слайд 26
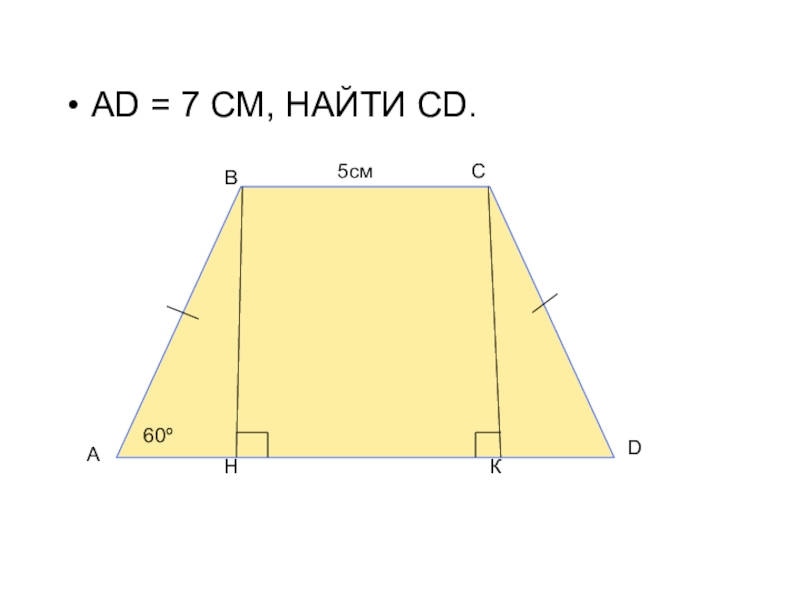
- 27. АD = 7 СМ, НАЙТИ CD.60º5смАВСDНК
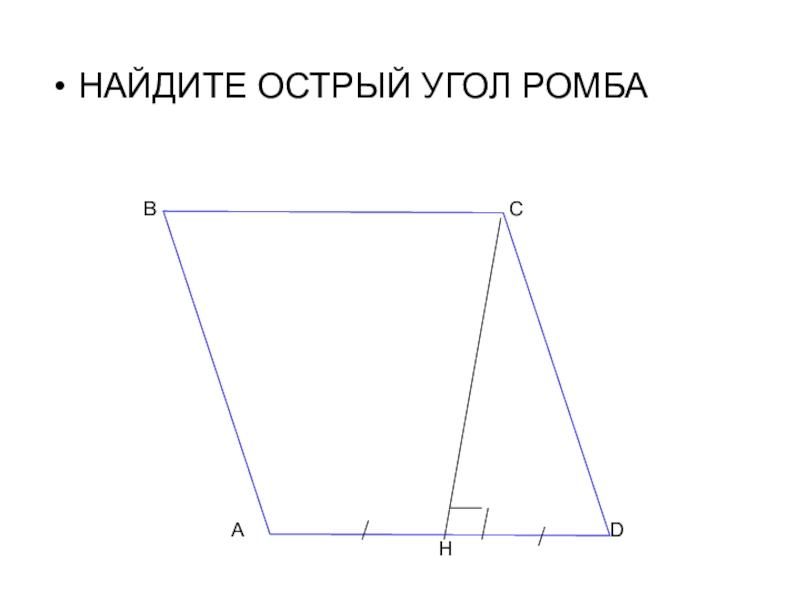
- 28. НАЙДИТЕ ОСТРЫЙ УГОЛ РОМБААВСDН
- 29. ДОМАШНЕЕ ЗАДАНИЕДано: АВСD – трапеция.АВ =
МУЛЬТИМЕДИЙНАЯ ПРЕЗЕНТАЦИЯ.ПЛАН УРОКА.1.ОБЪЯВЛЕНИЕ ТЕМЫ УРОКА.2. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ.3.ПРОВЕРКА ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА.4. РЕШЕНИЕ ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ.5.САМОСТОЯТЕЛЬНАЯ РАБОТА В ФОРМЕ ТЕСТОВ.6. ДОМАШНЕЕ ЗАДАНИЕ.
Слайд 1
ЛИЦЕЙ
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
УРОКА ПО ГЕОМЕТРИИ В 8 КЛАССЕ
ТЕМА : ЧЕТЫРЕХУГОЛЬНИКИ.
УЧИТЕЛЬ: ДУНДУКОВА
Слайд 2
МУЛЬТИМЕДИЙНАЯ ПРЕЗЕНТАЦИЯ.
ПЛАН УРОКА.
1.ОБЪЯВЛЕНИЕ ТЕМЫ УРОКА.
2. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ.
3.ПРОВЕРКА ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА.
4. РЕШЕНИЕ
ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ.
5.САМОСТОЯТЕЛЬНАЯ РАБОТА В ФОРМЕ ТЕСТОВ.
6. ДОМАШНЕЕ ЗАДАНИЕ.
5.САМОСТОЯТЕЛЬНАЯ РАБОТА В ФОРМЕ ТЕСТОВ.
6. ДОМАШНЕЕ ЗАДАНИЕ.
Слайд 3
ТЕМА УРОКА: ИТОГОВЫЙ УРОК ПО ТЕМЕ: «ЧЕТЫРЕХУГОЛЬНИКИ».
ЦЕЛЬ УРОКА: ЗАКРЕПЛЕНИЕ В ПРОЦЕССЕ РЕШЕНИЯ ЗАДАЧ ПОЛУЧЕННЫЕ ЗНАНИЯ И НАВЫКИ ПО ТЕМЕ, ПОДГОТОВИТЬ УЧАЩИХСЯ К КОНТРОЛЬНОЙ РАБОТЕ.
Слайд 5
Домашняя
работа
Задача:Найдите периметр прямоугольника АВСD, если
биссектрисы углов А и D делят сторону ВС на три отрезка, длина каждого из которых равна 4 см.
Дано: АВСD – прямоугольник,
АF биссектриса,
DЕ – биссектриса,
ВЕ = ЕF = FC = 4 cм.
Найти: РАВСD.
Решение.
Так как АF – биссектриса угла А, то АВF-равнобедренный
( FAD = AFB – накрест лежащие при AD ВС и АF – секущая) ВЕ = АВ = 8 см. Т.к. ВЕ = ЕF= FС = 4 см, то
ВС = 12 см. РАВСD = ( АВ + ВС )∙2. РАВСD = ( 8 + 12 ) ∙2 = 40см
Ответ: 40 см.
Задача:Найдите периметр прямоугольника АВСD, если
биссектрисы углов А и D делят сторону ВС на три отрезка, длина каждого из которых равна 4 см.
Дано: АВСD – прямоугольник,
АF биссектриса,
DЕ – биссектриса,
ВЕ = ЕF = FC = 4 cм.
Найти: РАВСD.
Решение.
Так как АF – биссектриса угла А, то АВF-равнобедренный
( FAD = AFB – накрест лежащие при AD ВС и АF – секущая) ВЕ = АВ = 8 см. Т.к. ВЕ = ЕF= FС = 4 см, то
ВС = 12 см. РАВСD = ( АВ + ВС )∙2. РАВСD = ( 8 + 12 ) ∙2 = 40см
Ответ: 40 см.
А
В
С
D
Е
F
Слайд 6
2.ПРОВЕРКА ИЗУЧЕННОГО МАТЕРИАЛА.
МЫ ЗАКОНЧИЛИ ИЗУЧЕНИЕ ТЕМЫ «ЧЕТЫРЕХУГОЛЬНИКИ», СЕГОДНЯ
У НАС
ИТОГОВЫЙ УРОК ПО ЭТОЙ ТЕМЕ.
ИТАК, ЧЕТЫРЕХУГОЛЬНИК - ЭТО ….( ДАТЬ ОПРЕДЕЛЕНИЕ).
НА ЭКРАНЕ ДАНЫ ФИГУРЫ, НАЗОВИТЕ НОМЕРА ФИГУР, КОТОРЫЕ ЯВЛЯЮТСЯ ЧЕТЫРЕХУГОЛЬНИКАМИ.
КАК НАЗЫВАЮТСЯ ТАКИЕ ФИГУРЫ?
ИТОГОВЫЙ УРОК ПО ЭТОЙ ТЕМЕ.
ИТАК, ЧЕТЫРЕХУГОЛЬНИК - ЭТО ….( ДАТЬ ОПРЕДЕЛЕНИЕ).
НА ЭКРАНЕ ДАНЫ ФИГУРЫ, НАЗОВИТЕ НОМЕРА ФИГУР, КОТОРЫЕ ЯВЛЯЮТСЯ ЧЕТЫРЕХУГОЛЬНИКАМИ.
КАК НАЗЫВАЮТСЯ ТАКИЕ ФИГУРЫ?
Слайд 9
ЧТО НАЗЫВАЕТСЯ ПАРАЛЛЕЛОГРАММОМ ?
ПЕРЕЧИСЛИТЬ ЕГО СВОЙСТВА.
ДИАГОНАЛЬ ПАРАЛЛЕЛОГРАММА РАЗБИВАЕТ
ЕГО НА ДВА ТРЕУГОЛЬНИКА,
ЧТО МОЖНО О НИХ СКАЗАТЬ? ПОЧЕМУ?
ДИАГОНАЛИ ПАРАЛЛЕЛОГРАММА РАВНЫ ?
ПОЧЕМУ?
ДИАГОНАЛИ ПАРАЛЛЕЛОГРАММА РАВНЫ ?
ПОЧЕМУ?
Слайд 11
ЧТО НАЗЫВАЕТСЯ ПРЯМОУГОЛЬНИКОМ ?
ПЕРЕЧИСЛИТЬ ЕГО СВОЙСТВА .
ДОКАЗАТЬ, ЧТО ДИАГОНАЛИ ПРЯМОУГОЛЬ-
НИКА РАВНЫ.
ПРОЧИТАТЬ
ПРИЗНАК ПАРАЛЛЕЛОГРАММА.
Слайд 17
ЧТО НАЗЫВАЕТСЯ ТРАПЕЦИЕЙ?
КАКИЕ ВИДЫ ТРАПЕЦИЙ ВЫ ЗНАЕТЕ?
КАКАЯ ТРАПЕЦИЯ НАЗЫВАЕТСЯ РАВНОБЕДРЕННОЙ?
КАКИМИ СВОЙСТВАМИ
ОБЛАДАЕТ РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ?
Слайд 23
ИТАК, МЫ ДОКАЗАЛИ, ЧТО БИССЕКТРИСА
УГЛА ПАРАЛЛЕЛОГРАММА ОТСЕКАЕТ ОТ
НЕГО
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК.
ВЕРНО ЛИ ЭТО УТВЕРЖДЕНИЕ ДЛЯ ДРУ –
ГИХ ВИДОВ ЧЕТЫРЕХУГОЛЬНИКОВ ?
ВЕРНО ЛИ ЭТО УТВЕРЖДЕНИЕ ДЛЯ ДРУ –
ГИХ ВИДОВ ЧЕТЫРЕХУГОЛЬНИКОВ ?
Слайд 24
ДАНО: АВСD – ПАРАЛЛЕЛОГРАММ, АМ – БИССЕКТРИСА УГЛА А. ДОКАЗАТЬ, ЧТО
ТРЕУГОЛЬНИК АВМ – РАВНОБЕДРЕННЫЙ
А
В
С
D
1
1
м
2
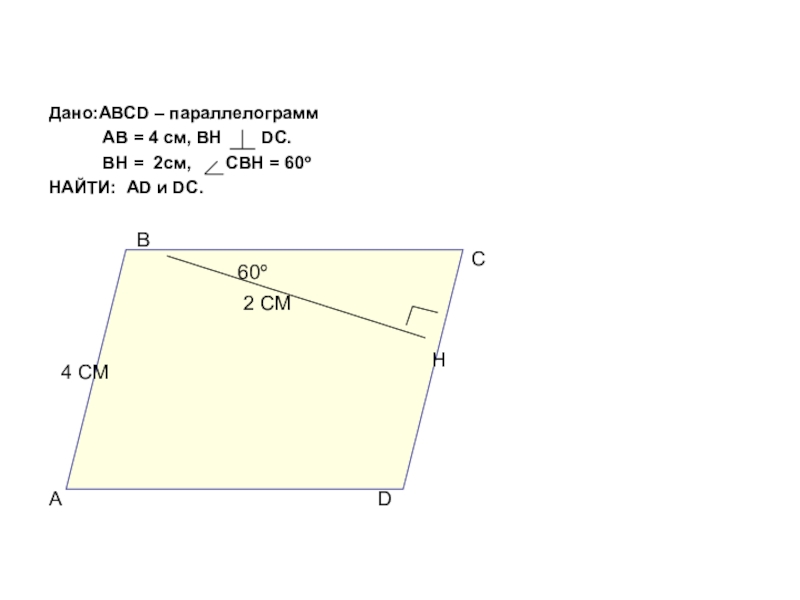
Слайд 26
Дано:АВСD – параллелограмм
АВ = 4 см, ВН DC.
ВН = 2см, СВН = 60º
НАЙТИ: АD и DC.
А
В
С
D
H
60º
2 CМ
4 CМ