- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок по геометрии Сумма углов треугольника
Содержание
- 1. Урок по геометрии Сумма углов треугольника
- 2. Цель урока: развивать навыки самоконтроля
- 3. «Нет ничего дороже для человека того, чтобы хорошо мыслить». Л. Толстой
- 4. ЛУГО МЕРЕОТА КУЛЬРИНГОТЕРасшифруйте анаграммы:
- 5. Теорема о сумме углов треугольникаДоказательствоABCСумма углов треугольника
- 6. Теорема о внешнем угле треугольника Дано: ∆
- 7. 1
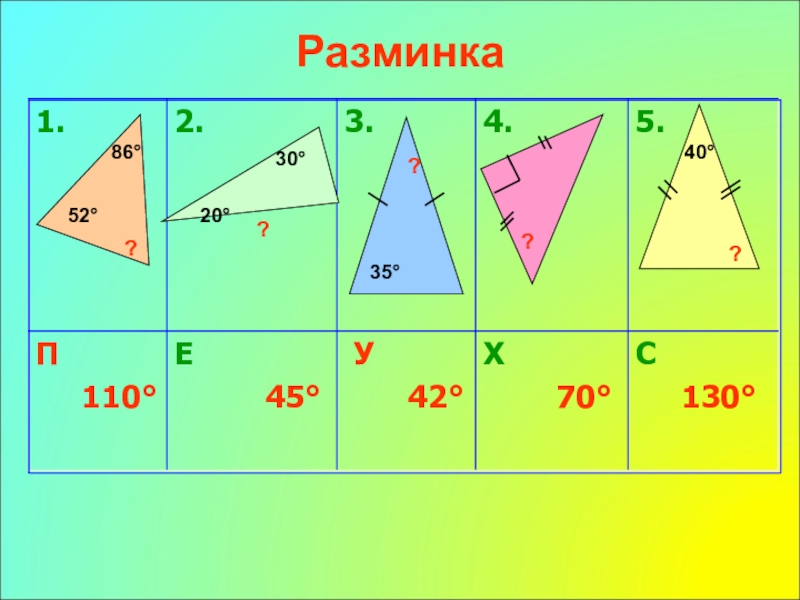
- 8. Разминка 52°86°?20°30°?35°40°???
- 9. Проверь себя:Критерии оценки:«2» - менее трёх заданий,«3»
- 10. N 1.В ∆ АВС ∠А=75° , ∠В меньше ∠С в 6 раз. Найти ∠В, ∠С.
- 11. № 224Дано: ∠А: ∠В: ∠С= 2:3:4∠А=2х, Найти:
- 12. Домашнее задание: № 227 (б), № 235
- 13. Слайд 13
Цель урока: развивать навыки самоконтроля и взаимоконтроля; закрепить и проверить знания и умения учащихся по данной теме.
Слайд 2Цель урока:
развивать навыки самоконтроля и взаимоконтроля;
закрепить и проверить
знания и умения
учащихся по данной теме.
учащихся по данной теме.
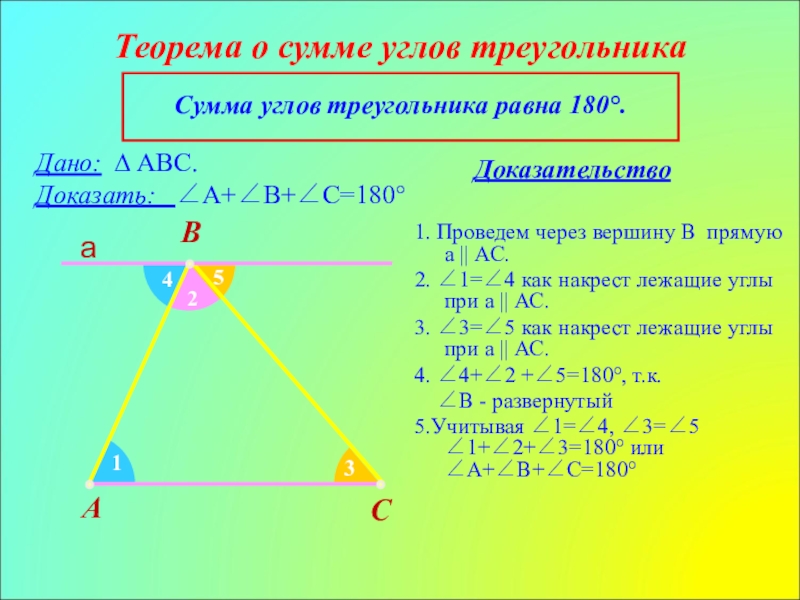
Слайд 5Теорема о сумме углов треугольника
Доказательство
A
B
C
Сумма углов треугольника равна 180°.
4
5
Дано: ∆ АВС.
Доказать:
∠А+∠В+∠С=180°
1. Проведем через вершину В прямую а || AC.
2. ∠1=∠4 как накрест лежащие углы при a || АС.
3. ∠3=∠5 как накрест лежащие углы при a || АС.
4. ∠4+∠2 +∠5=180°, т.к.
∠В - развернутый
5.Учитывая ∠1=∠4, ∠3=∠5 ∠1+∠2+∠3=180° или ∠А+∠В+∠С=180°
1
2
3
а
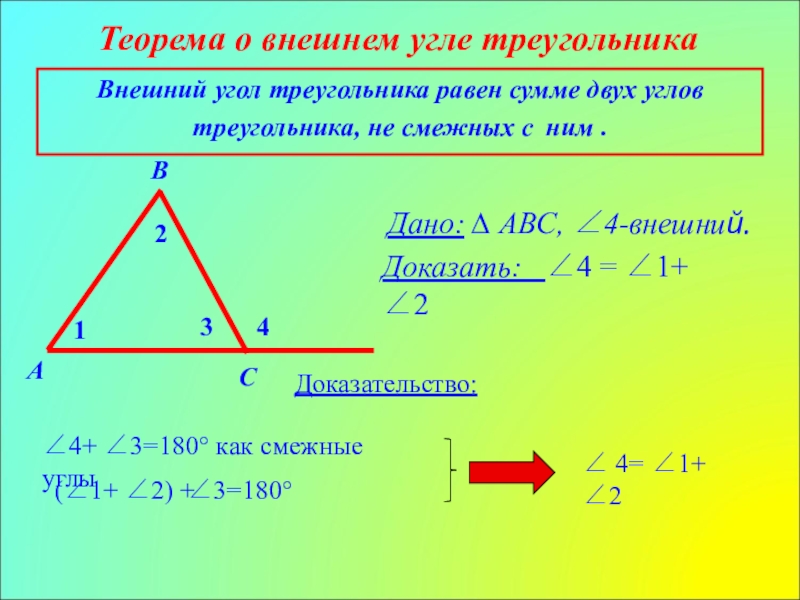
Слайд 6Теорема о внешнем угле треугольника
Дано: ∆ АВС, ∠4-внешний.
1
2
3
4
Доказать: ∠4
= ∠1+ ∠2
Доказательство:
∠4+ ∠3=180° как смежные углы
(∠1+ ∠2) +
∠3=180°
∠ 4= ∠1+ ∠2
A
В
С
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним .
Слайд 9Проверь себя:
Критерии оценки:
«2» - менее трёх заданий,
«3» - 3 задания, «4»
- 4 задания, «5» - 5 заданий.
Слайд 11№ 224
Дано: ∠А: ∠В:
∠С= 2:3:4
∠А=2х,
Найти: ∠А, ∠В,
∠С
Решение:
Пусть Х – 1 часть,
∠С=4х
∠В=3х ,
Т.к.
∠А+∠В+ ∠С= 180°, то составим уравнение:
2х+3х+4х = 180 °
9х =180 °
х = 20 ° - 1 часть
∠А=20° · 2 = 40°
∠В=20° · 3 = 60 °
∠С= 20° · 4 = 80°
Ответ: ∠А=40°, ∠В=60 °, ∠С= 80°
