- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок №14 Глава2, п.15.Решение задач на применение 1 признака равенства треугольников
Содержание
- 1. Урок №14 Глава2, п.15.Решение задач на применение 1 признака равенства треугольников
- 2. Слайд 2
- 3. Проверка Д.Р № 12 на 19.10.18
- 4. Стр.31,№95 Дано:ВС=АD,АD=17см,DC=14сма) Доказать: ∆ABC=∆CDA;б)Найти: AB,BCРешение:а) ∆ABC=∆CDA
- 5. Слайд 5
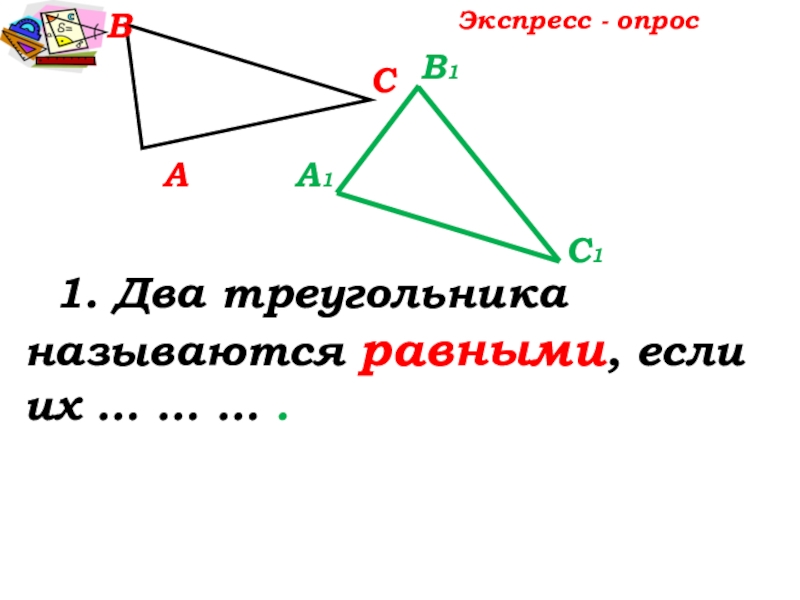
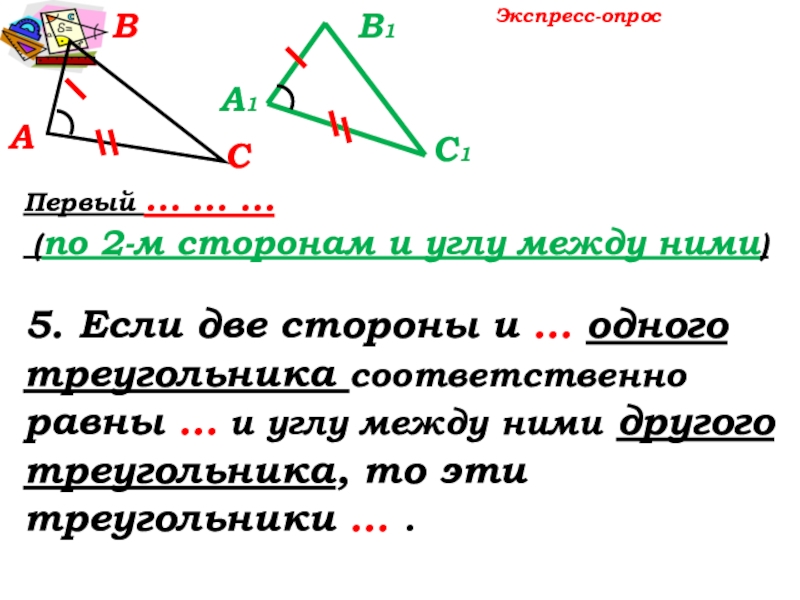
- 6. АВСЭкспресс - опрос 1. Два треугольника называются равными, если их … … … .А1С1В1
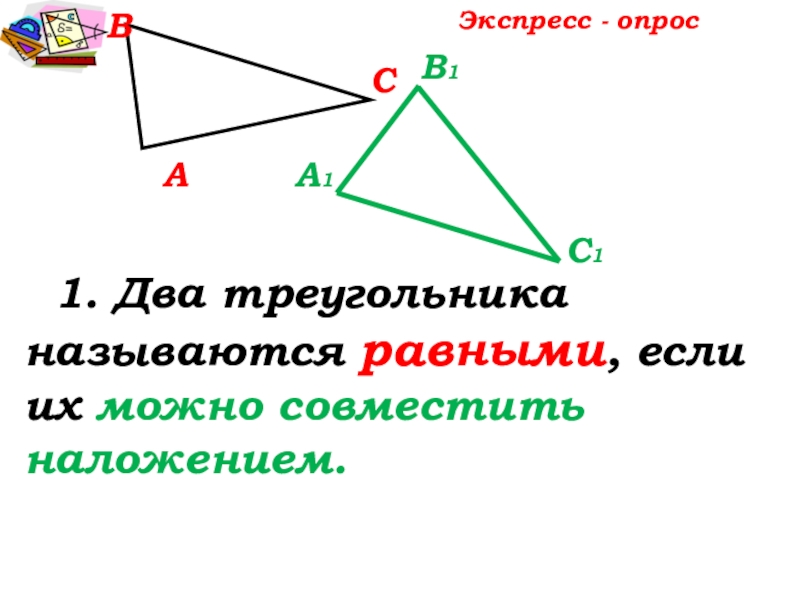
- 7. АВС 1. Два треугольника называются равными, если их можно совместить наложением.А1С1В1Экспресс - опрос
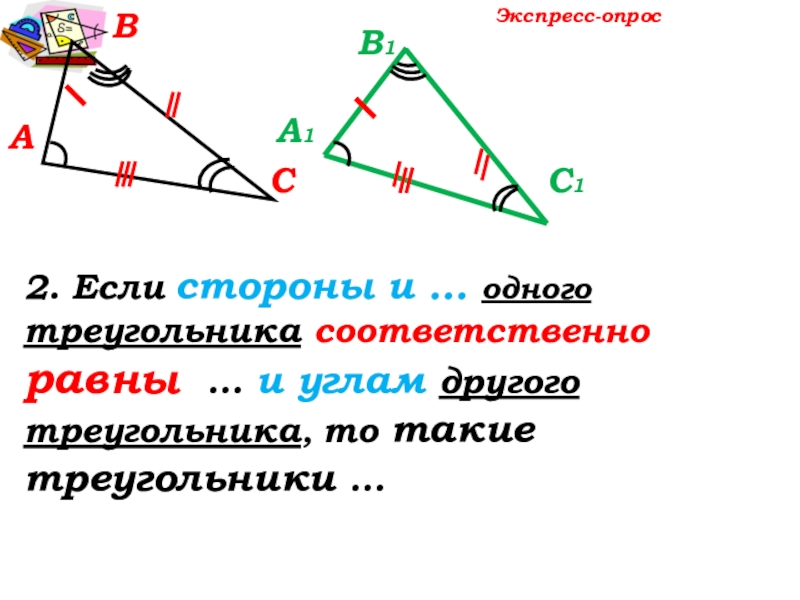
- 8. АВСЭкспресс-опрос2. Если стороны и … одного треугольника
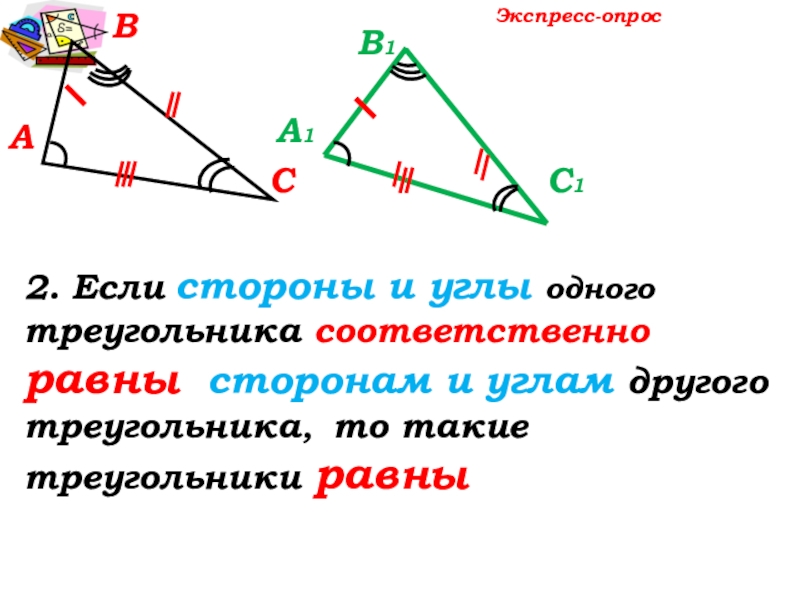
- 9. АВСЭкспресс-опрос2. Если стороны и углы одного треугольника
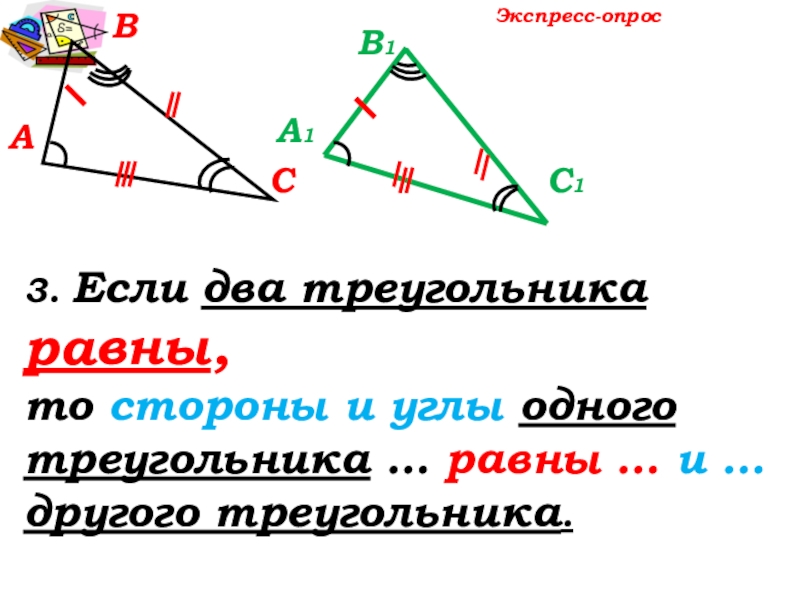
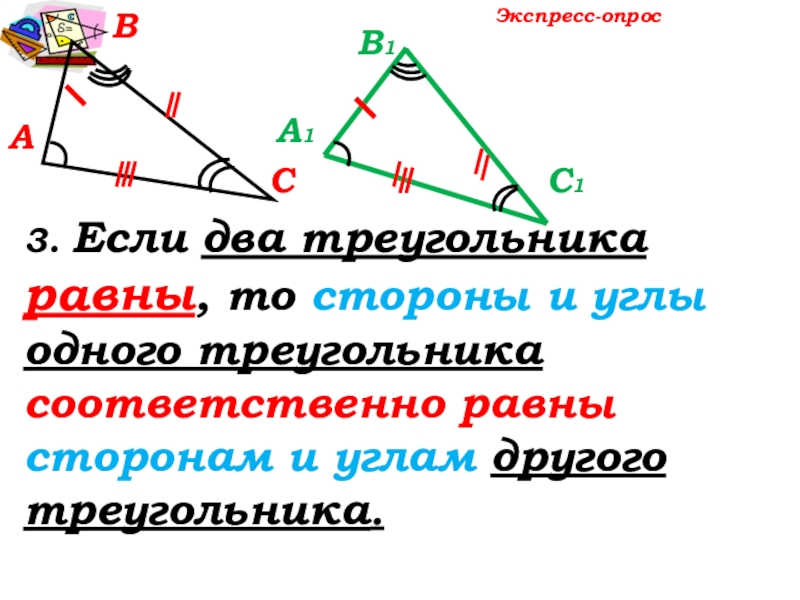
- 10. АВСЭкспресс-опрос3. Если два треугольника равны, то стороны
- 11. АВСЭкспресс-опрос3. Если два треугольника равны, то стороны
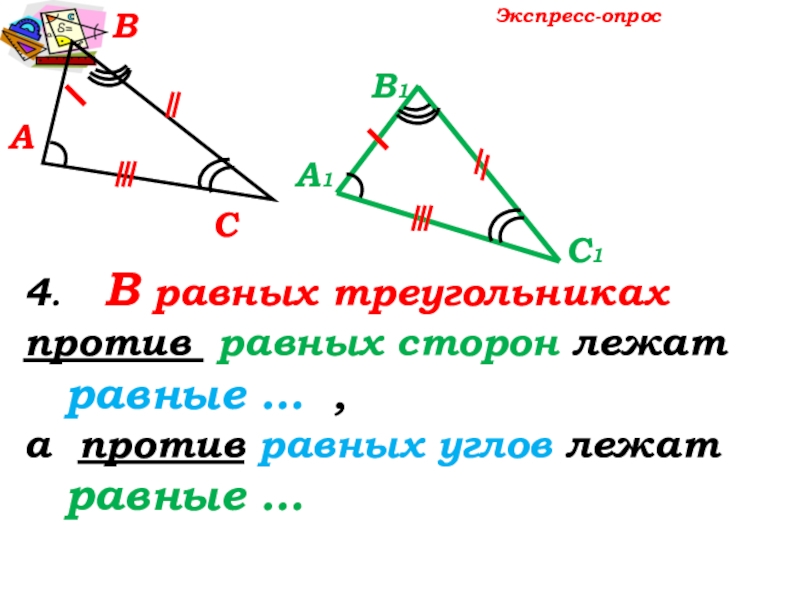
- 12. АВСА1С1В14. В равных треугольниках против равных
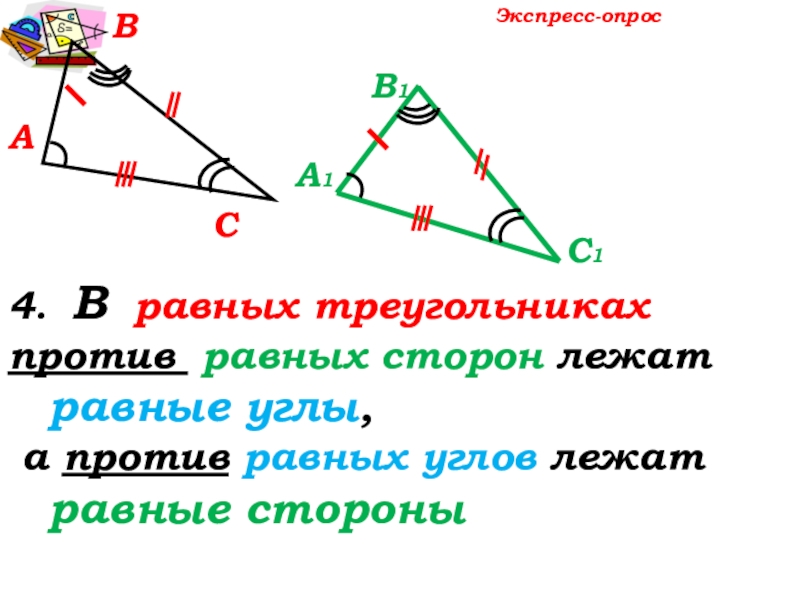
- 13. АВСА1С1В14. В равных треугольниках против равных сторон
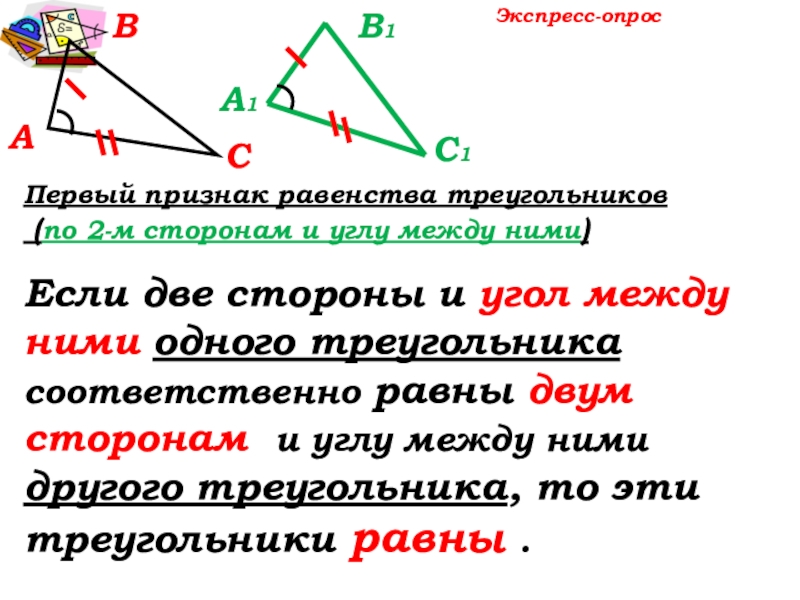
- 14. АВСА1С1В1Первый … … … (по 2-м сторонам
- 15. АВСА1С1В1Первый признак равенства треугольников (по 2-м сторонам
- 16. Решение задач. п15.19.10.2018К.Р.
- 17. Цели урока:Учиться решать задачи на применение первого
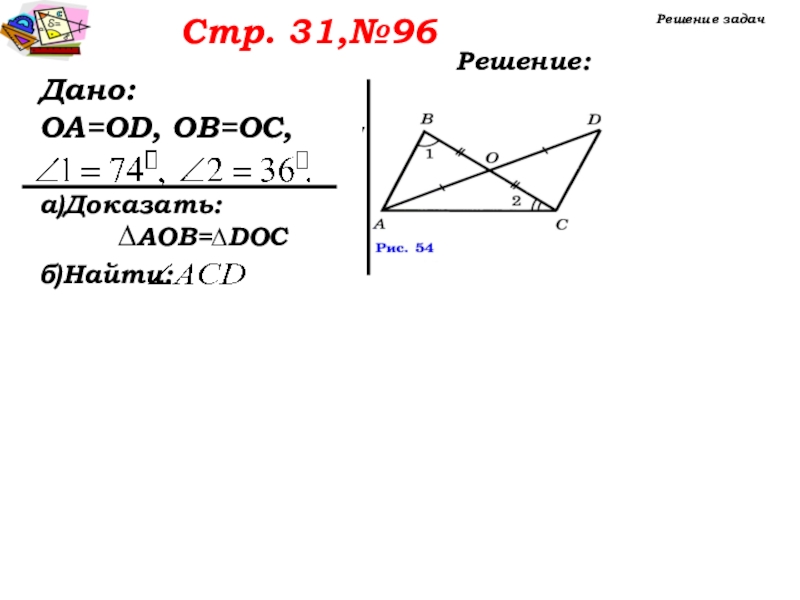
- 18. Решение задачСтр. 31,№96Прочитайте задачу.Что следует записать в «Дано».
- 19. Стр. 31,№96Решение задачРешение: Дано:
- 20. Стр. 31,№96Решение задачРешение: Дано:OA=OD,OB=OC,Доказать:
- 21. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОС
- 22. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСИмеют ли ∆AОВ и ∆DОС равные элементы?
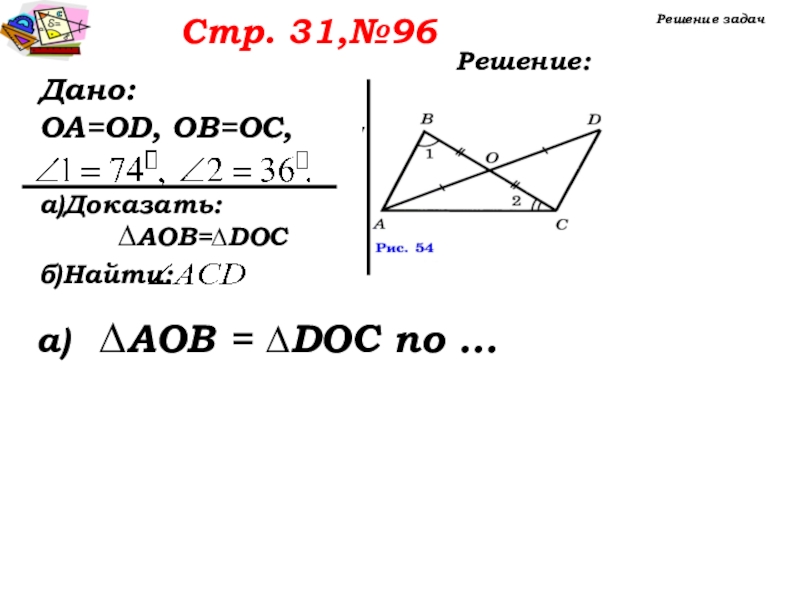
- 23. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСа) ∆AОВ = ∆DОС по …
- 24. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСа) ∆AОВ = ∆DОС по 1 признаку равенства треугольников, по…
- 25. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСа) ∆AОВ =
- 26. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСа) ∆AОВ =
- 27. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСб) Из равенства треугольников ∆AОВ и ∆DОС имеем:
- 28. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСб) Из равенства треугольников ∆AОВ и ∆DОС имеем:
- 29. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСб) Из равенства треугольников ∆AОВ и ∆DОС имеем:
- 30. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСб) Из равенства
- 31. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСб) Из равенства
- 32. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСб) Из равенства
- 33. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСб) Из равенства
- 34. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСб) Из равенства
- 35. Стр. 31,№96Решение задачРешение: Дано:OA=OD, OB=OC,а)Доказать:б)Найти:∆AОВ=∆DОСб) Из равенства
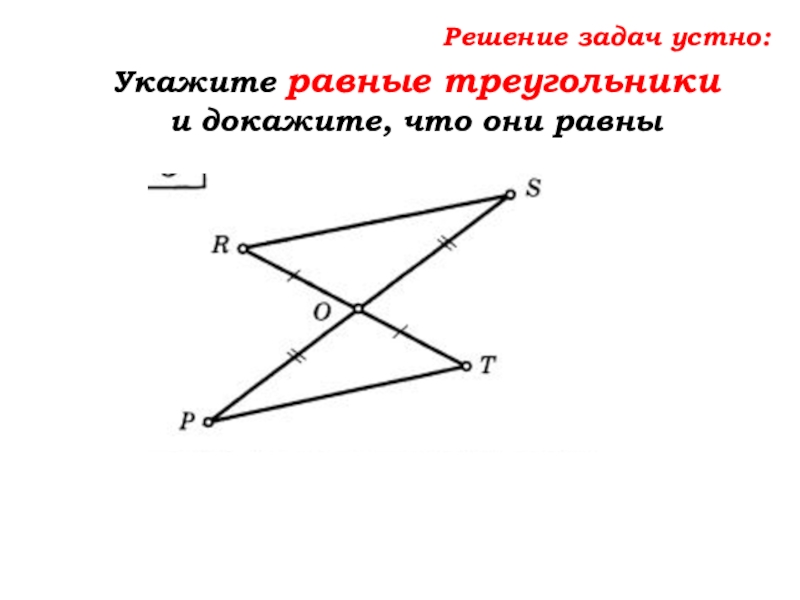
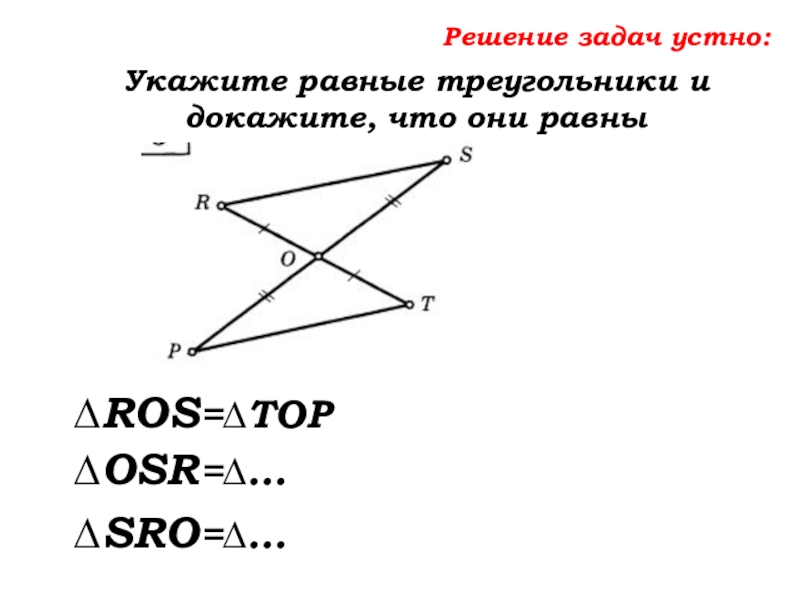
- 36. Решение задач устно:Укажите равные треугольники и докажите, что они равны
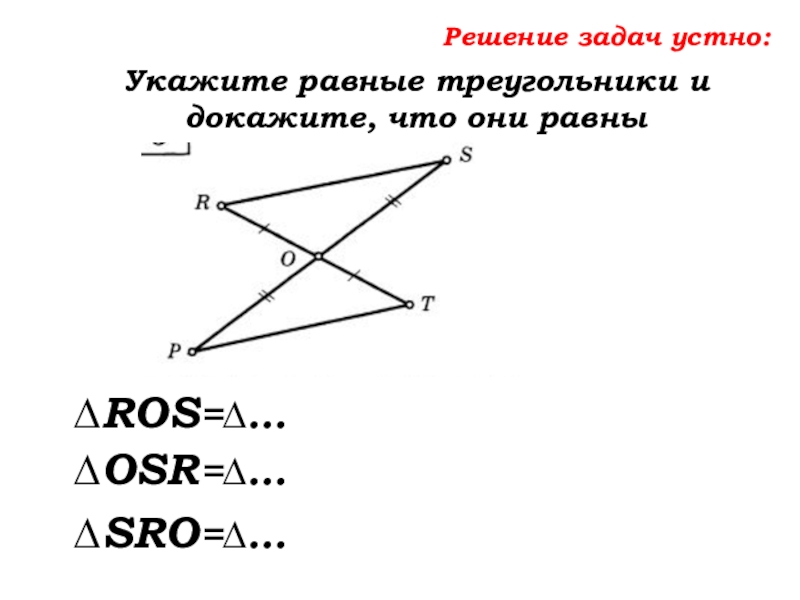
- 37. Решение задач устно:Укажите равные треугольники и докажите, что они равны∆ROS=∆…∆OSR=∆…∆SRO=∆…
- 38. Решение задач устно:Укажите равные треугольники и докажите, что они равны∆ROS=∆TOP∆OSR=∆…∆SRO=∆…
- 39. Решение задач устно:Укажите равные треугольники и докажите, что они равны∆ROS=∆TOP∆OSR=∆OPT∆SRO=∆…
- 40. Решение задач устно:Укажите равные треугольники и докажите, что они равны∆ROS=∆TOP∆OSR=∆OPT∆SRO=∆PTO
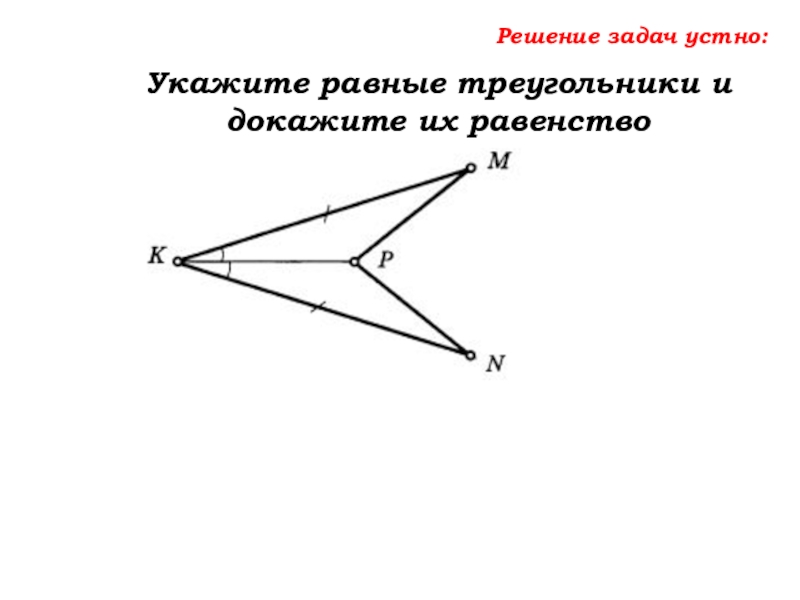
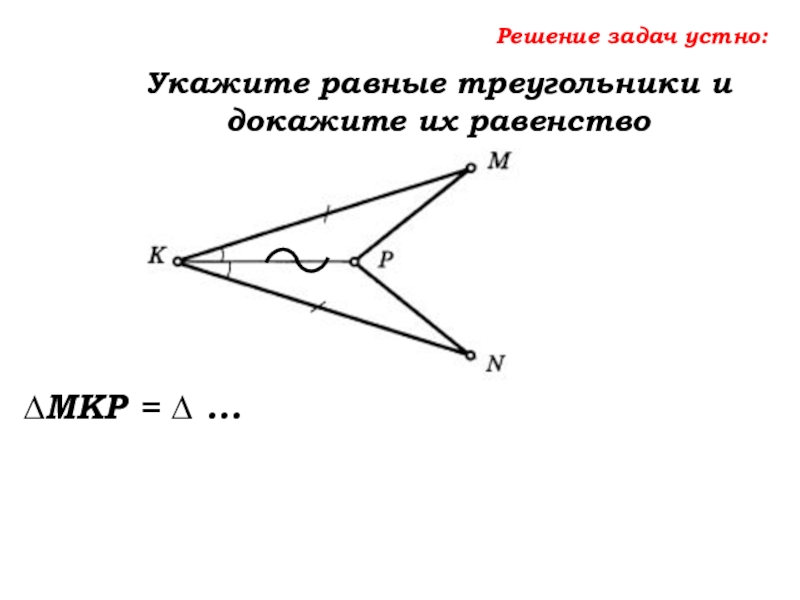
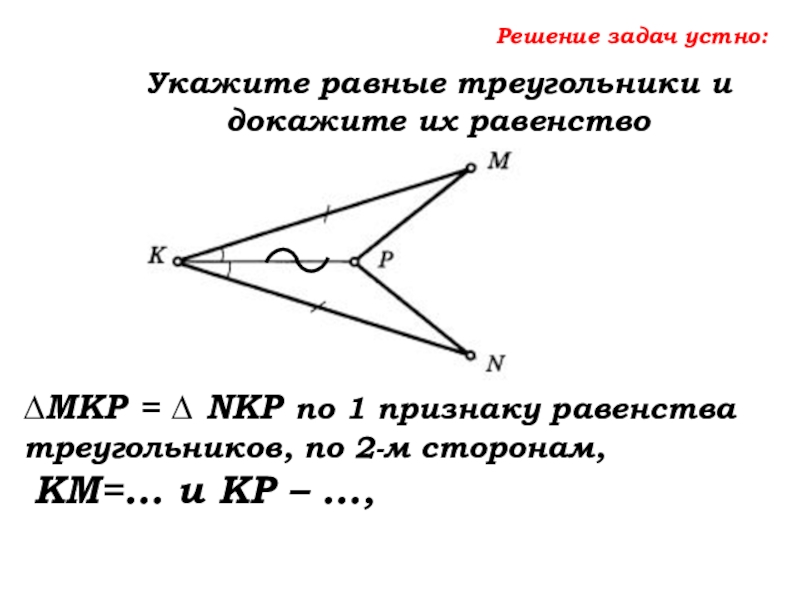
- 41. Решение задач устно:Укажите равные треугольники и докажите их равенство
- 42. Решение задач устно:Укажите равные треугольники и докажите их равенство∆MKP = ∆ …
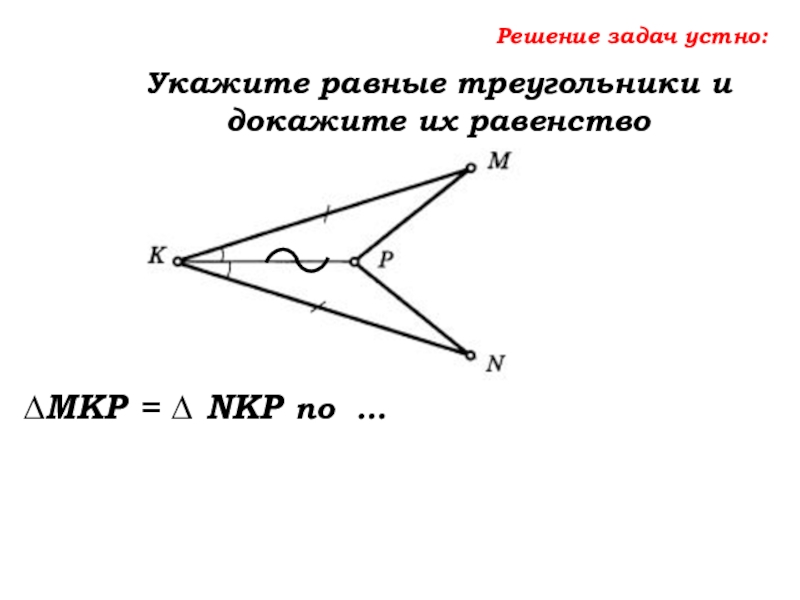
- 43. Решение задач устно:Укажите равные треугольники и докажите их равенство∆MKP = ∆ NKP по …
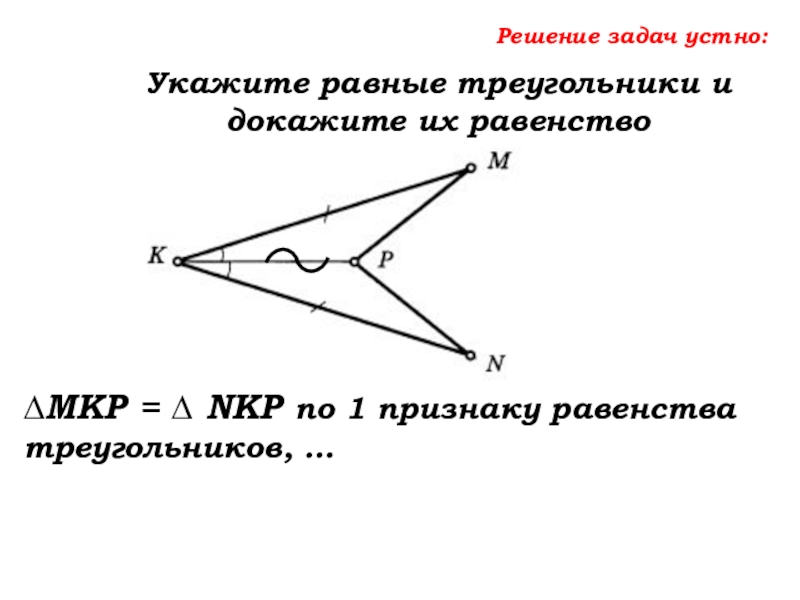
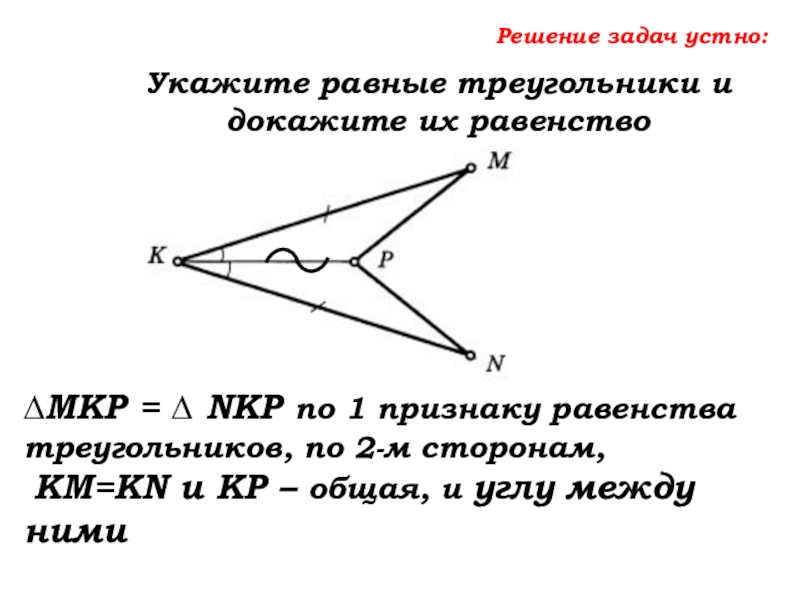
- 44. Решение задач устно:Укажите равные треугольники и докажите
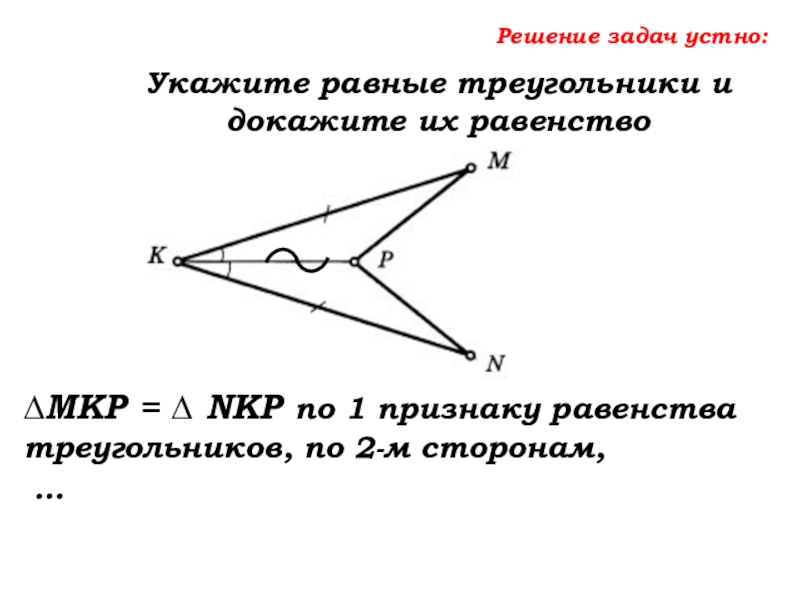
- 45. Решение задач устно:Укажите равные треугольники и докажите
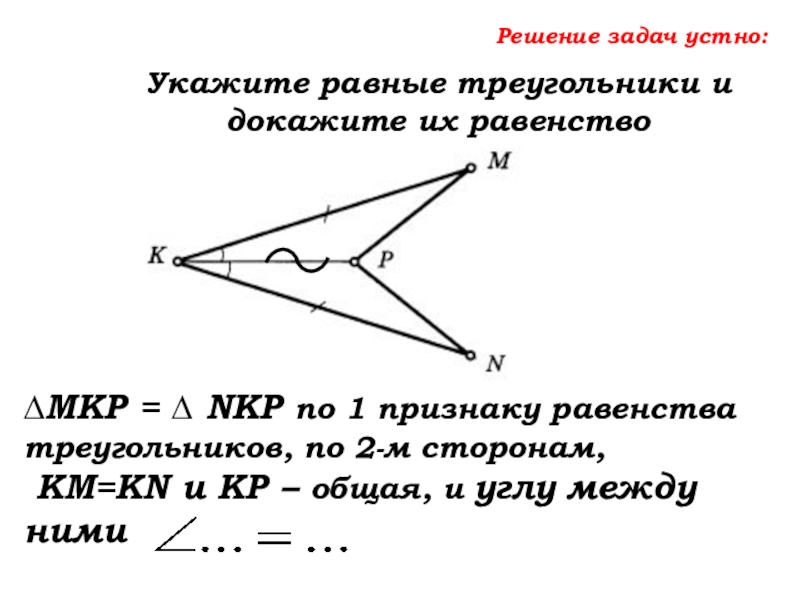
- 46. Решение задач устно:Укажите равные треугольники и докажите
- 47. Решение задач устно:Укажите равные треугольники и докажите
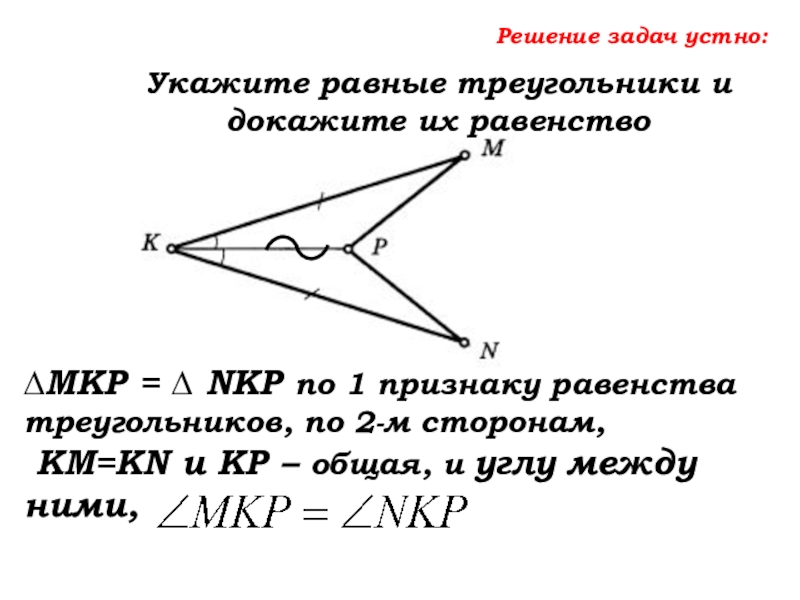
- 48. Решение задач устно:Укажите равные треугольники и докажите
- 49. Решение задач устно:Укажите равные треугольники и докажите
- 50. Стр.31, №97* Д.Р
- 51. Стр.31, №97* Д.Р
- 52. Стр.31, №97* Д.Р
- 53. Стр.31, №97* Д.Р
- 54. Стр.31, №97* Д.Р
- 55. Стр.31, №97* Д.Р
- 56. Стр.31, №97* Д.Р
- 57. Итоги урокаС.Р.
- 58. Итоги
- 59. Итоги урока Оцените свое настроение по итогам урока: Все понятно Остались некоторые вопросы Требуетсяпомощь
- 60. Д.Р № 13 на 24.10.18Учить зачётные вопросы,конспект
Слайд 2
Успешного усвоения нового материала
Основная мысль урока
Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи,
то решайте их. (Д.Пойа)
Слайд 4Стр.31,№95
Дано:
ВС=АD,
АD=17см,
DC=14см
а) Доказать:
∆ABC=∆CDA;
б)Найти: AB,BC
Решение:
а) ∆ABC=∆CDA по первому признаку равенства
по двум сторонам (ВC=АD и AC-общая) и углу между ними( ).
б) ВC=АD=17см.
В равных треугольниках против равных углов, , лежат равные стороны AB=DC=14см.
Ответ: AB=14см, ВC=17см.
Д.Р № 12 на 19.10.18
C
Слайд 5
Слайд 7
А
В
С
1. Два треугольника называются равными, если их можно совместить наложением.
А1
С1
В1
Экспресс
Слайд 8
А
В
С
Экспресс-опрос
2. Если стороны и … одного треугольника соответственно равны … и
А1
С1
В1
Слайд 9
А
В
С
Экспресс-опрос
2. Если стороны и углы одного треугольника соответственно равны сторонам и
А1
С1
В1
Слайд 10
А
В
С
Экспресс-опрос
3. Если два треугольника равны,
то стороны и углы одного треугольника
А1
С1
В1
Слайд 11
А
В
С
Экспресс-опрос
3. Если два треугольника равны, то стороны и углы одного треугольника
А1
С1
В1
Слайд 12
А
В
С
А1
С1
В1
4. В равных треугольниках
против равных сторон лежат
равные
а против равных углов лежат
равные …
Экспресс-опрос
Слайд 13
А
В
С
А1
С1
В1
4. В равных треугольниках
против равных сторон лежат
равные углы,
равные стороны
Экспресс-опрос
Слайд 14
А
В
С
А1
С1
В1
Первый … … …
(по 2-м сторонам и углу между
5. Если две стороны и … одного треугольника соответственно равны … и углу между ними другого треугольника, то эти треугольники … .
Экспресс-опрос
Слайд 15
А
В
С
А1
С1
В1
Первый признак равенства треугольников
(по 2-м сторонам и углу между ними)
Если
Экспресс-опрос
Слайд 17Цели урока:
Учиться решать задачи на применение первого признака равенства треугольников.
Формировать
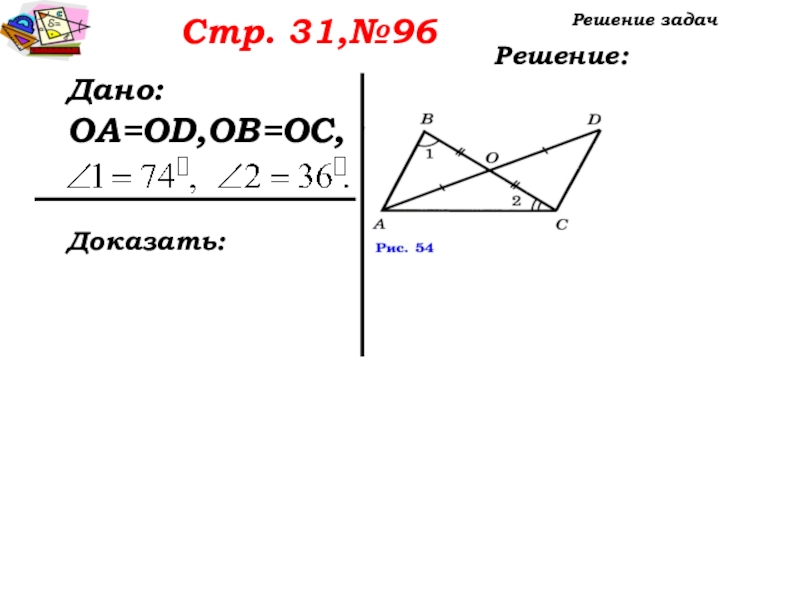
Слайд 22Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
Имеют ли ∆AОВ и ∆DОС равные элементы?
Слайд 23Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
а) ∆AОВ = ∆DОС по …
Слайд 24Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
а) ∆AОВ = ∆DОС по 1 признаку
Слайд 25Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
а) ∆AОВ = ∆DОС по 1 признаку
Слайд 26Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
а) ∆AОВ = ∆DОС по 1 признаку
Слайд 27Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
б) Из равенства треугольников ∆AОВ и ∆DОС
Слайд 28Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
б) Из равенства треугольников ∆AОВ и ∆DОС
Слайд 29Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
б) Из равенства треугольников ∆AОВ и ∆DОС
Слайд 30Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
б) Из равенства треугольников ∆AОВ и ∆DОС
Слайд 31Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
б) Из равенства треугольников ∆AОВ и ∆DОС
Тогда
Слайд 32Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
б) Из равенства треугольников ∆AОВ и ∆DОС
Тогда
Слайд 33Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
б) Из равенства треугольников ∆AОВ и ∆DОС
Тогда
Слайд 34Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
б) Из равенства треугольников ∆AОВ и ∆DОС
Тогда
Слайд 35Стр. 31,№96
Решение задач
Решение:
Дано:
OA=OD, OB=OC,
а)Доказать:
б)Найти:
∆AОВ=∆DОС
б) Из равенства треугольников ∆AОВ и ∆DОС
Тогда
Ответ: б)
Слайд 37Решение задач устно:
Укажите равные треугольники и докажите, что они равны
∆ROS=∆…
∆OSR=∆…
∆SRO=∆…
Слайд 38Решение задач устно:
Укажите равные треугольники и докажите, что они равны
∆ROS=∆TOP
∆OSR=∆…
∆SRO=∆…
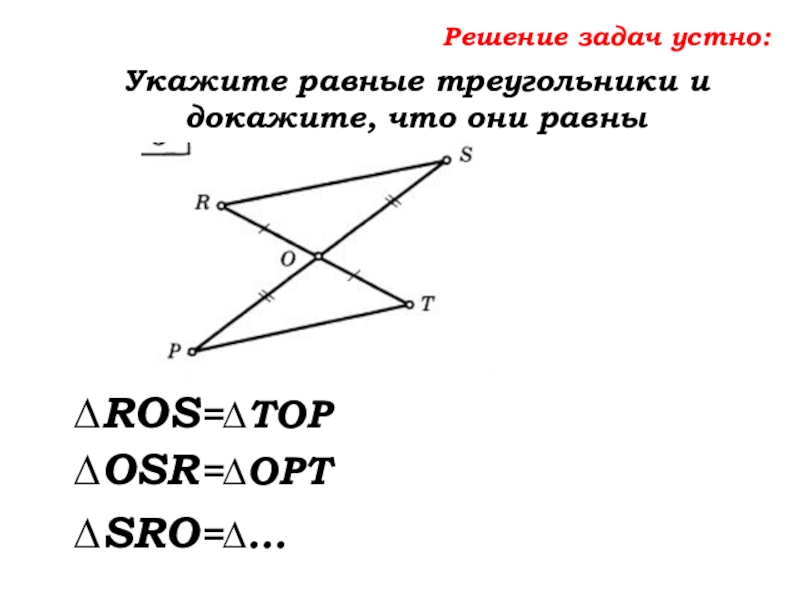
Слайд 39Решение задач устно:
Укажите равные треугольники и докажите, что они равны
∆ROS=∆TOP
∆OSR=∆OPT
∆SRO=∆…
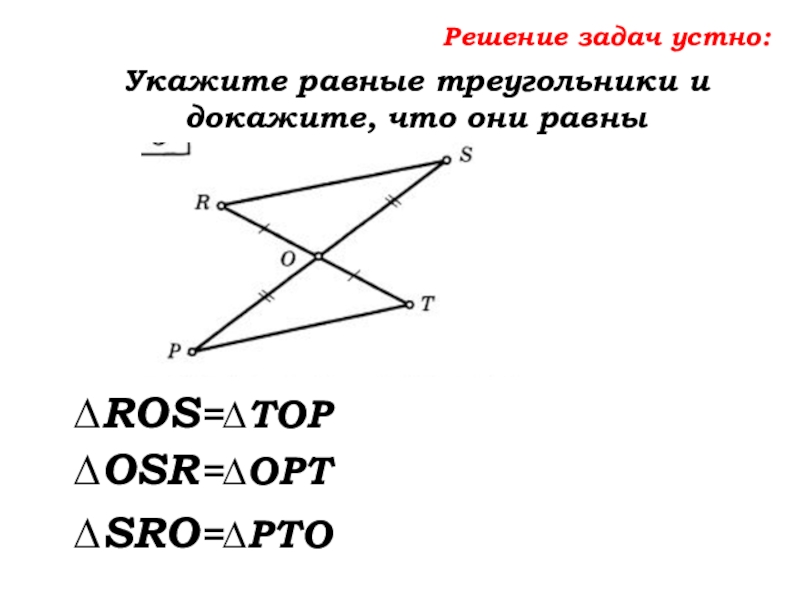
Слайд 40Решение задач устно:
Укажите равные треугольники и докажите, что они равны
∆ROS=∆TOP
∆OSR=∆OPT
∆SRO=∆PTO
Слайд 44Решение задач устно:
Укажите равные треугольники и докажите их равенство
∆MKP = ∆
Слайд 45Решение задач устно:
Укажите равные треугольники и докажите их равенство
∆MKP = ∆
…
Слайд 46Решение задач устно:
Укажите равные треугольники и докажите их равенство
∆MKP = ∆
KM=… и KP – …,
Слайд 47Решение задач устно:
Укажите равные треугольники и докажите их равенство
∆MKP = ∆
KM=KN и KP – общая, и углу между ними
Слайд 48Решение задач устно:
Укажите равные треугольники и докажите их равенство
∆MKP = ∆
KM=KN и KP – общая, и углу между ними
Слайд 49Решение задач устно:
Укажите равные треугольники и докажите их равенство
∆MKP = ∆
KM=KN и KP – общая, и углу между ними,
Слайд 50
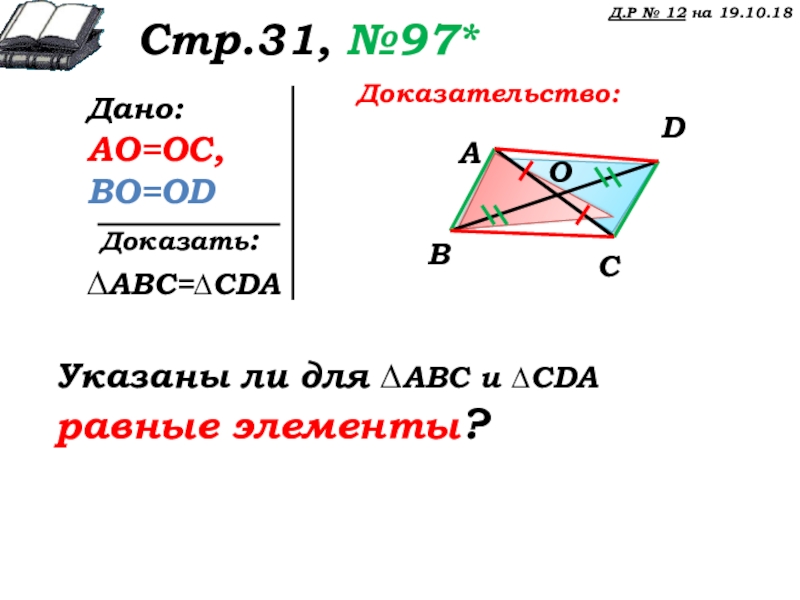
Стр.31, №97*
Д.Р № 12 на 19.10.18
A
C
B
D
O
Дано:
AO=OC,
BO=OD
∆ABC=∆CDA
Доказательство:
Указаны ли для ∆ABC и ∆CDA равные элементы?
Слайд 51
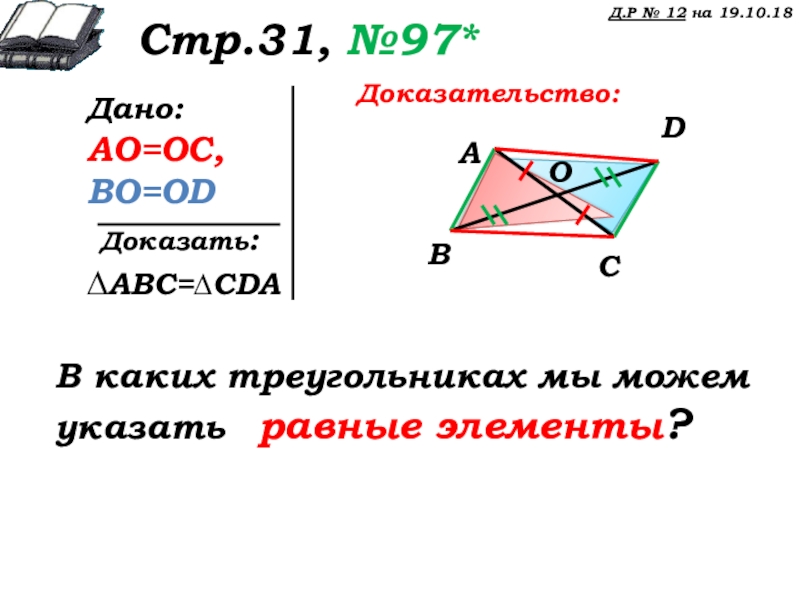
Стр.31, №97*
Д.Р № 12 на 19.10.18
A
C
B
D
O
Дано:
AO=OC,
BO=OD
∆ABC=∆CDA
Доказательство:
В каких треугольниках мы можем указать равные элементы?
Слайд 52
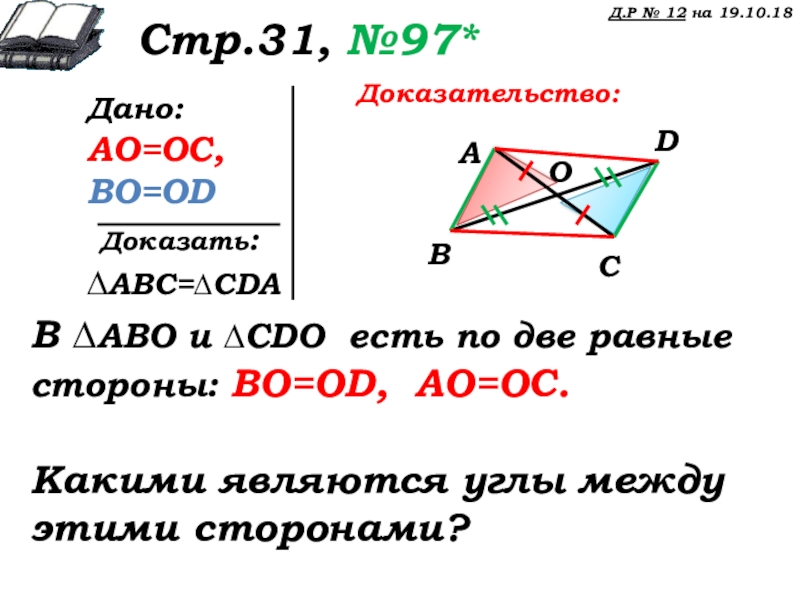
Стр.31, №97*
Д.Р № 12 на 19.10.18
A
C
B
D
O
Дано:
AO=OC,
BO=OD
∆ABC=∆CDA
Доказательство:
В ∆ABО и ∆CDО есть по две равные стороны: ВО=ОD, AO=OC.
Какими являются углы между этими сторонами?
Слайд 53
Стр.31, №97*
Д.Р № 12 на 19.10.18
A
C
B
D
O
Дано:
AO=OC,
BO=OD
∆ABC=∆CDA
Доказательство:
В ∆ABО и ∆CDО есть по две равные стороны: ВО=ОD, AO=OC и углы
между этими сторонами равны,
, как вертикальные
1
2
Слайд 54
Стр.31, №97*
Д.Р № 12 на 19.10.18
A
C
B
D
O
Дано:
AO=OC,
BO=OD
∆ABC=∆CDA
Доказательство:
1) ∆ABО= ∆CDО по 1 признаку равенства треугольников, по 2 сторонам, ВО=ОD, AO=OC, и углу между ними, .
2)
1
2
Слайд 55
Стр.31, №97*
Д.Р № 12 на 19.10.18
A
C
B
D
O
Дано:
AO=OC,
BO=OD
∆ABC=∆CDA
Доказательство:
1) ∆ABО= ∆CDО по 1 признаку равенства треугольников, по 2 сторонам, ВО=ОD, AO=OC, и углу между ними, .
2) Из равенства треугольников: ∆ABО= ∆CDО, имеем: АВ=СD,
3
4
Слайд 56
Стр.31, №97*
Д.Р № 12 на 19.10.18
A
C
B
D
O
Дано:
AO=OC,
BO=OD
∆ABC=∆CDA
Доказательство:
2) Из равенства треугольников: ∆ABО=∆CDО, имеем: АВ=СD ,
3) ∆ABC=∆CDA по 1 признаку равенства треугольников, по 2 сторонам, АВ=СD и АС-общая, и углу между ними .
Что требовалось доказать.
3
4
Слайд 59Итоги урока
Оцените свое настроение по итогам урока:
Все понятно
Остались некоторые вопросы
Требуется
помощь
Слайд 60
Д.Р № 13 на 24.10.18
Учить зачётные вопросы,
конспект урока разобрать,
Стр.31,№92,93, №97*
Иметь
набор геом. инструментов.