- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок геометрии в 9 классе Длина окружности
Содержание
- 1. Урок геометрии в 9 классе Длина окружности
- 2. Цели урока:Вывести формулу для вычисления длины окружности;Научить учащихся решать задачи на применение формулы длины окружности
- 3. Чтобы получить наглядное представление о длине окружности,
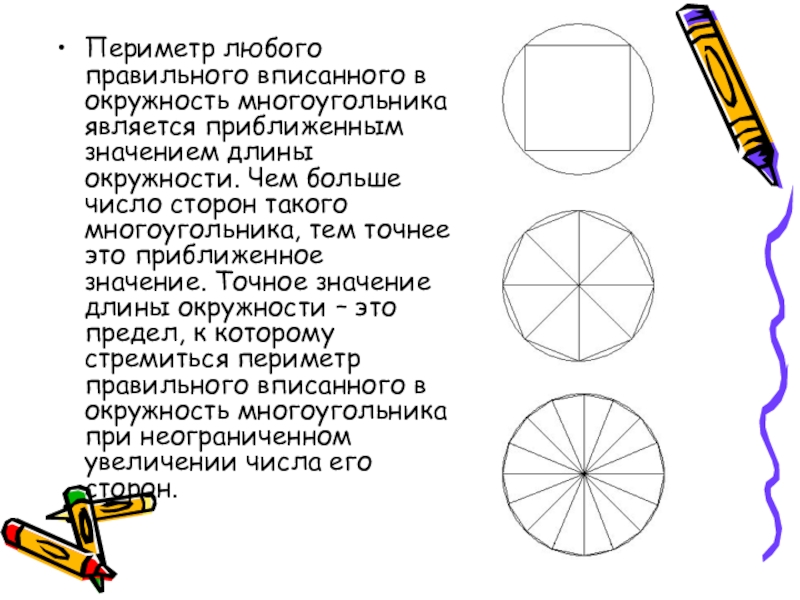
- 4. Периметр любого правильного вписанного в окружность многоугольника
- 5. Выведем формулу, выражающую длину окружности через её
- 6. Это равенство будет выполнятся при любом значении
- 7. Из равенства C/2R=П получаем формулу для вычисления
- 8. Выведем теперь формулу для вычисления дуги l
- 9. Закрепление изученного материала:№1103,№1104(а), №1105(б,г),№72, №74из рабочей тетради
- 10. Домашнее заданиеП.110,№1104(д),№1105(в),№77 из рабочей тетради.
Цели урока:Вывести формулу для вычисления длины окружности;Научить учащихся решать задачи на применение формулы длины окружности
Слайд 2Цели урока:
Вывести формулу для вычисления длины окружности;
Научить учащихся решать задачи на
применение формулы длины окружности
Слайд 3Чтобы получить наглядное представление о длине окружности, представим себе, что окружность
сделана из тонкой нерастяжимой нити. Если мы разрежем нить в какой-нибудь точке А и распрямим её, то получим отрезок АА1, длина которого и есть длина окружности.
А
А1
Слайд 4Периметр любого правильного вписанного в окружность многоугольника является приближенным значением длины
окружности. Чем больше число сторон такого многоугольника, тем точнее это приближенное значение. Точное значение длины окружности – это предел, к которому стремиться периметр правильного вписанного в окружность многоугольника при неограниченном увеличении числа его сторон.
Слайд 5Выведем формулу, выражающую длину окружности через её радиус. Пусть С и
С1 – длины окружностей радиусов R и R1. Впишем в каждую из них правильный n-угольник и обозначим через Pn и Pn1 их периметры. Используя формулу, получаем:
Pn=nxan=nx2Rxsin180/n,
Pn1=nxan 1 =nx2R1xsin180/n.
Следовательно,
Pn/P1n=2R/2R1 (1)
Pn=nxan=nx2Rxsin180/n,
Pn1=nxan 1 =nx2R1xsin180/n.
Следовательно,
Pn/P1n=2R/2R1 (1)
Слайд 6Это равенство будет выполнятся при любом значении n. Будем теперь неограниченно
увеличивать число n. Так как P C, P1 C1 при n, то предел отношения Pn/P1n равен C/C1. C другой стороны, в силу равенства (1) этот предел равен 2R/2R1. Таким образом, C/C1= 2R/2R1. Из этого равенства следует, что C/2R=C1/2R1, т.е. отношение длины окружности к её диаметру есть одно и то же число для всех окружностей. Это число принято обозначать буквой П.
Слайд 7Из равенства C/2R=П получаем формулу для вычисления длины окружности радиуса R:
C=2ПR.
Доказано, что П является бесконечной непериодической десятичной дробью, т.е. иррациональным числом. Рациональное число 22/7 является приближенным значением П с точностью до 0,002. Это приближенное значение было найдено ещё в III в. до н.э. великим греческим учёным Архимедом. При решении задач обычно пользуются приближенным значением П с точностью до 0,01 : П=3,14.
Слайд 8Выведем теперь формулу для вычисления дуги l окружности с градусной мерой
а. Так как длина всей окружности равна 2ПR, то длина дуги в 1 градус равна 2ПR/360=ПR/180.Поэтому длина l выражается формулой:
L=ПRxа/180.
L=ПRxа/180.