Жданов А.А. ©
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок геометрии в 8-м классе на тему Теорема Пифагора (ФГОС)
Содержание
- 1. Урок геометрии в 8-м классе на тему Теорема Пифагора (ФГОС)
- 2. Какой треугольник называется прямоугольным? (это треугольник, в
- 3. 1. Назовите стороны: •
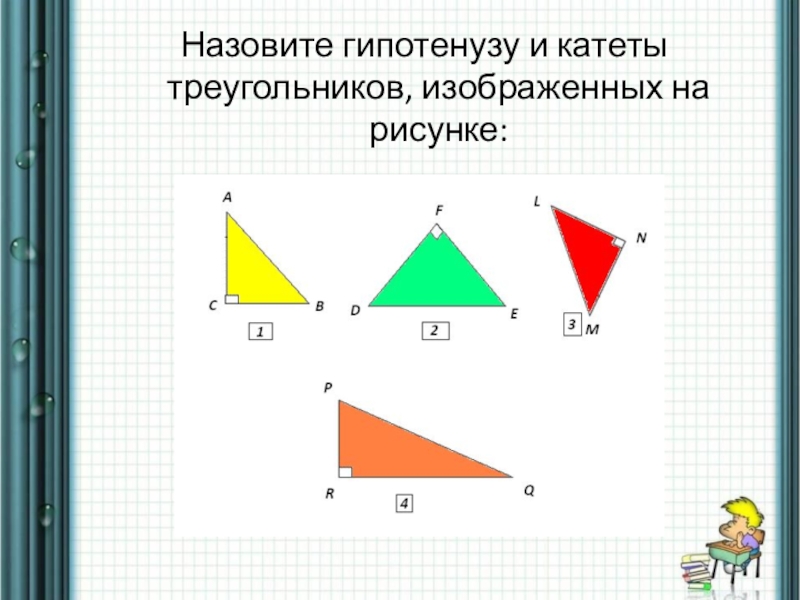
- 4. Назовите гипотенузу и катеты треугольников, изображенных на рисунке:
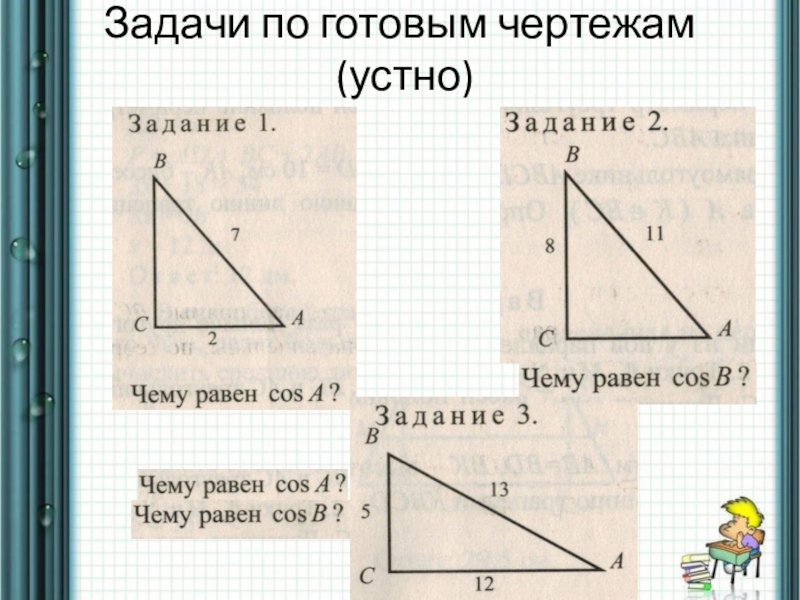
- 5. Задачи по готовым чертежам (устно)
- 6. Задание № 1 Постройте прямоугольный треугольник с заданными сторонами:
- 7. Кто построил треугольник с заданными сторонами?Какой вывод
- 8. Опираясь на данные таблицы, попробуйте установить
- 9. Действительно, существует определенное соотношение (связь) между сторонами
- 10. Теорема ПифагораВ прямоугольном треугольнике квадрат гипотенузы равен
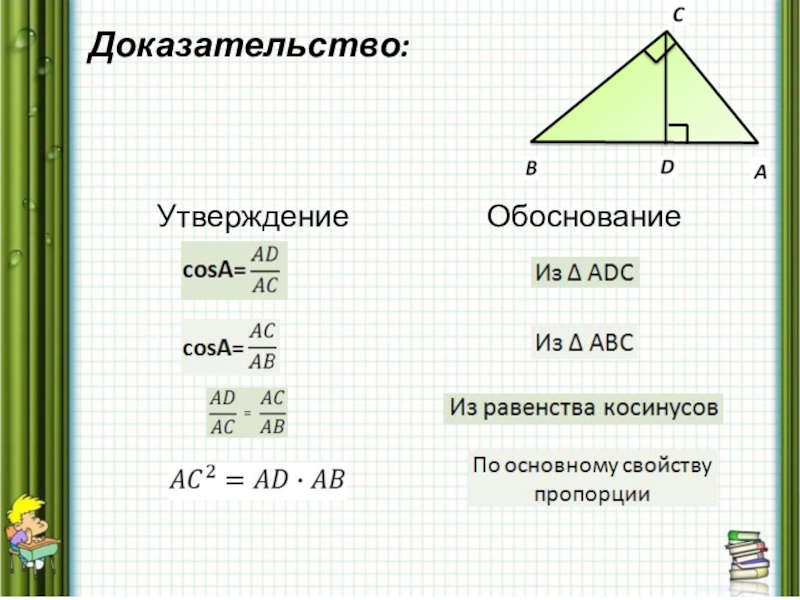
- 11. Доказательство:
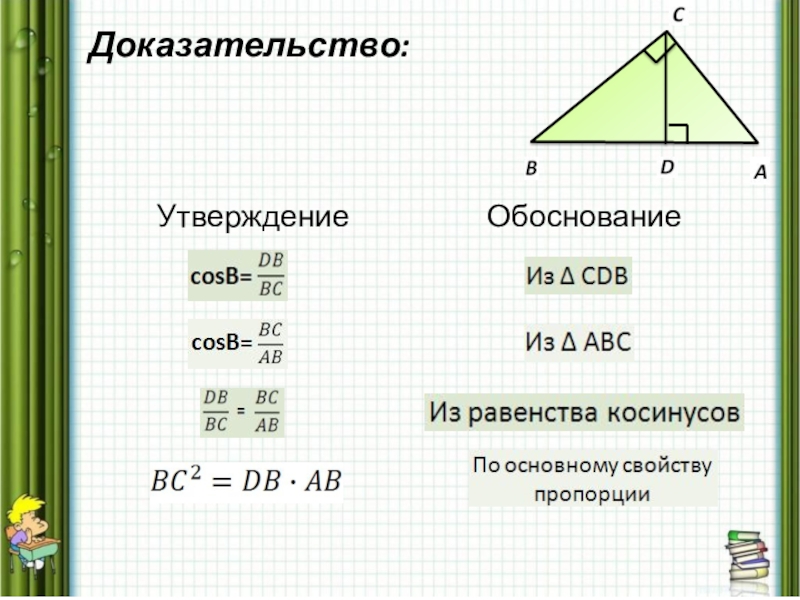
- 12. Доказательство:
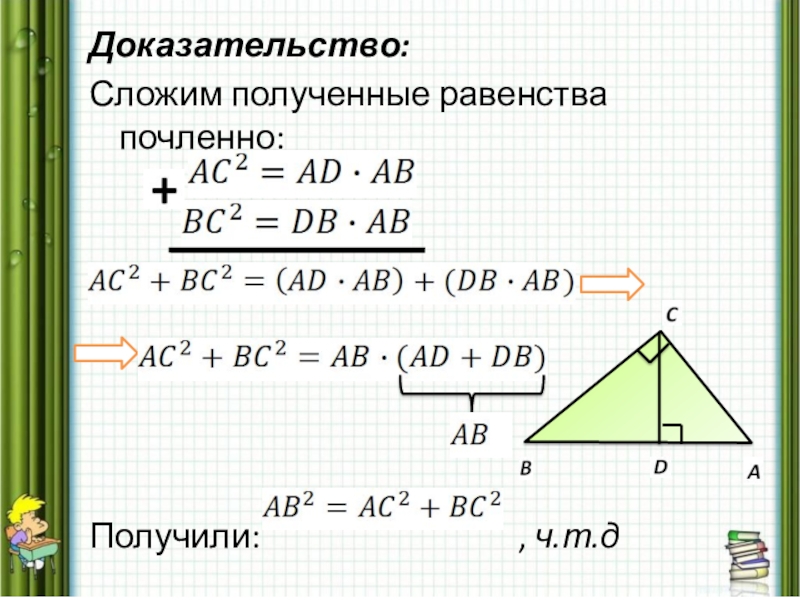
- 13. Доказательство:Сложим полученные равенства почленно:Получили:
- 14. Задача №1∆ ABC – прямоугольный. ВС =
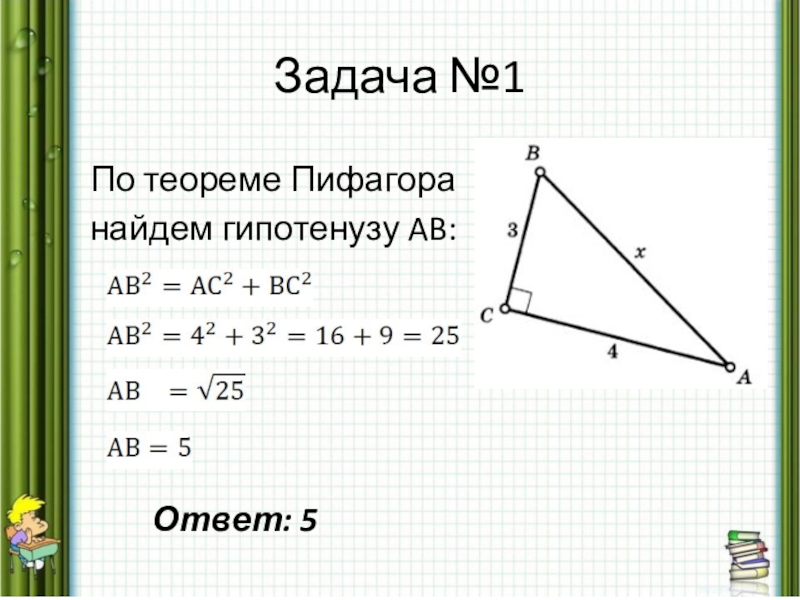
- 15. Задача №1 По теореме Пифагора найдем гипотенузу AB: Ответ: 5
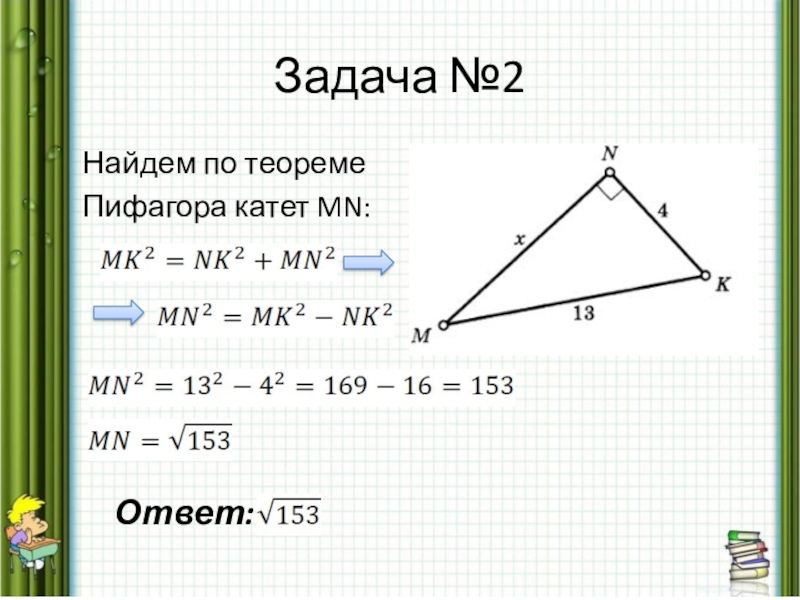
- 16. Задача №2 В прямоугольном треугольнике MNK известны
- 17. Задача №2 Найдем по теореме Пифагора катет MN: Ответ:
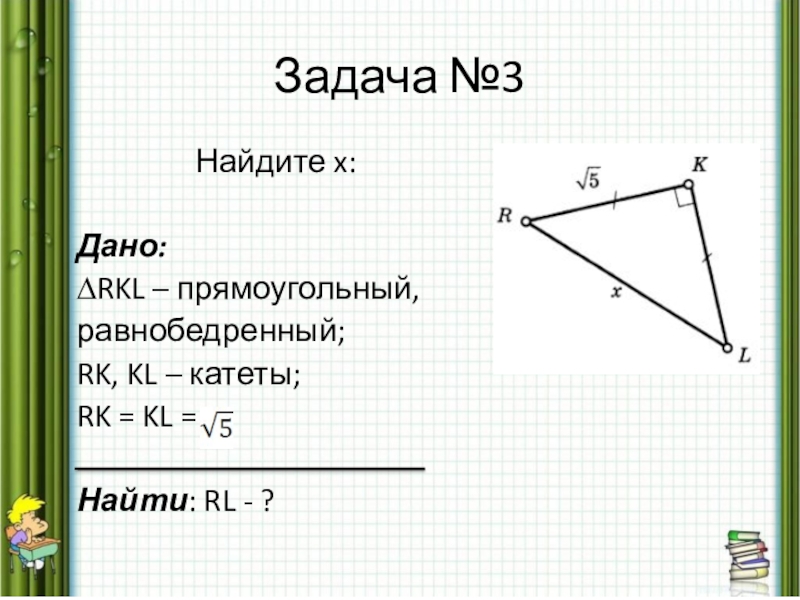
- 18. Задача №3
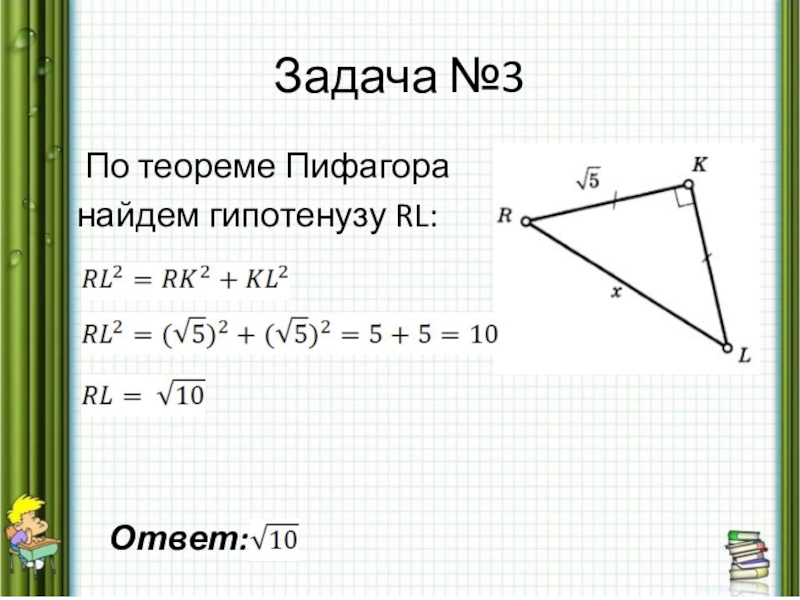
- 19. Задача №3 По теореме Пифагора найдем гипотенузу RL: Ответ:
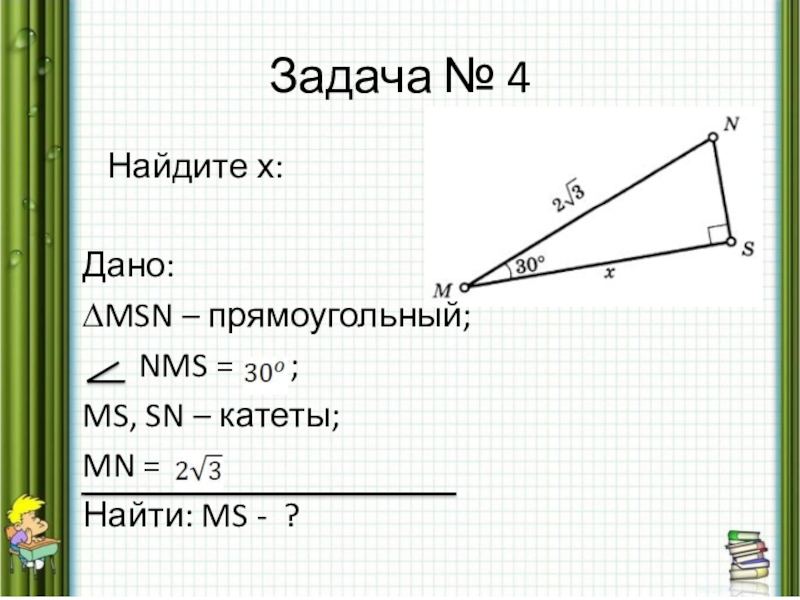
- 20. Задача № 4 Найдите х: Дано:
- 21. Задача № 4Найдем NS: NS =
- 22. Задача № 5Какой длины должна быть лестница,
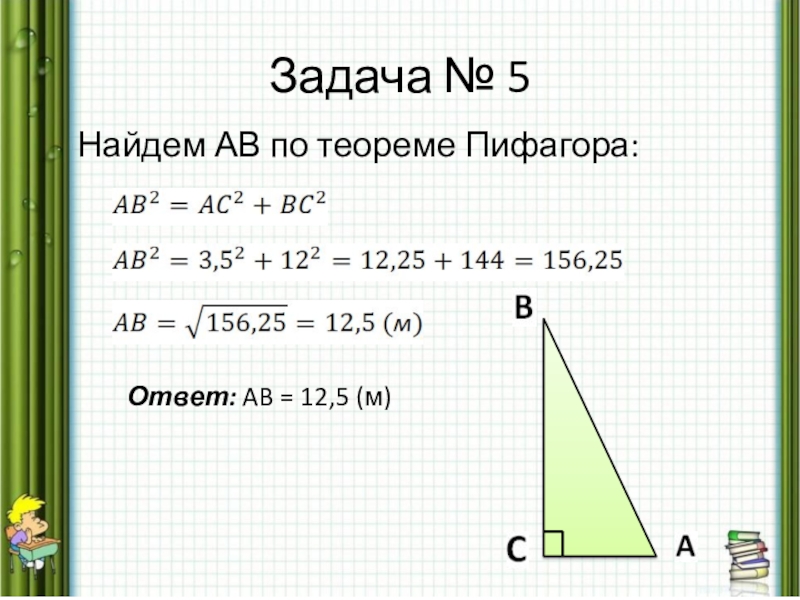
- 23. Задача № 5Найдем АВ по теореме Пифагора: Ответ: AB = 12,5 (м)
- 24. Домашнее задание Знать формулировку и доказательство теоремы
- 25. Спасибо за внимание!
Какой треугольник называется прямоугольным? (это треугольник, в котором один угол прямой (то есть составляет 90 градусов)Как называются стороны такого треугольника? (Катет, катет, гипотенуза)Где находится гипотенуза? (против прямого угла)От чего зависит и не зависит косинус? (Косинус угла
Слайд 1Теорема пифагора
Пифагор Самосский (570—490 гг. до н. э.) — древнегреческий философ, математик и
мистик, создатель религиозно-философской школы пифагорейцев.
Слайд 2Какой треугольник называется прямоугольным?
(это треугольник, в котором один угол прямой
(то есть составляет 90 градусов)
Как называются стороны такого треугольника?
(Катет, катет, гипотенуза)
Где находится гипотенуза?
(против прямого угла)
От чего зависит и не зависит косинус?
(Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.)
Что такое пропорция? Назовите основное свойство пропорции
(Пропорция – равенство двух отношений. Основное свойство: произведение крайних членов равно произведению средних).
Как называются стороны такого треугольника?
(Катет, катет, гипотенуза)
Где находится гипотенуза?
(против прямого угла)
От чего зависит и не зависит косинус?
(Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.)
Что такое пропорция? Назовите основное свойство пропорции
(Пропорция – равенство двух отношений. Основное свойство: произведение крайних членов равно произведению средних).
Слайд 3 1. Назовите стороны: • прилежащие к углу А •
противолежащие углу А
• прилежащие к углу В
• противолежащие углу В
2. назовите cos A, cos B (
2. назовите cos A, cos B (
Слайд 7Кто построил треугольник с заданными сторонами?
Какой вывод мы с вами сделаем?
В прямоугольном треугольнике между сторонами есть зависимость, его нельзя задать произвольным образом.
Измерьте получившиеся стороны. Средние результаты измерения занесите в таблицу:
Слайд 8 Опираясь на данные таблицы, попробуйте установить связь между сторонами треугольника
(катетами и гипотенузой) в каждом из случаев. Выскажите свои предположения.
Слайд 9Действительно, существует определенное соотношение (связь) между сторонами прямоугольного треугольника, которое первый
заметил и доказал Пифагор Самосский. Эта связь называется теоремой Пифагора.
Слайд 10Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано:
АВС – прямоугольный.
Доказать:
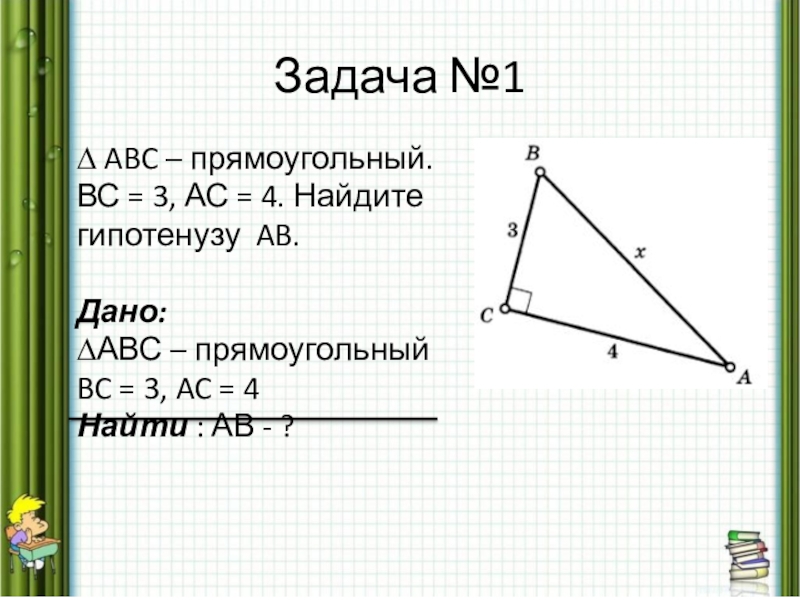
Слайд 14Задача №1
∆ ABC – прямоугольный.
ВС = 3, АС = 4.
Найдите
гипотенузу AB.
Дано:
∆АВС – прямоугольный
BC = 3, AC = 4
Найти : АВ - ?
гипотенузу AB.
Дано:
∆АВС – прямоугольный
BC = 3, AC = 4
Найти : АВ - ?
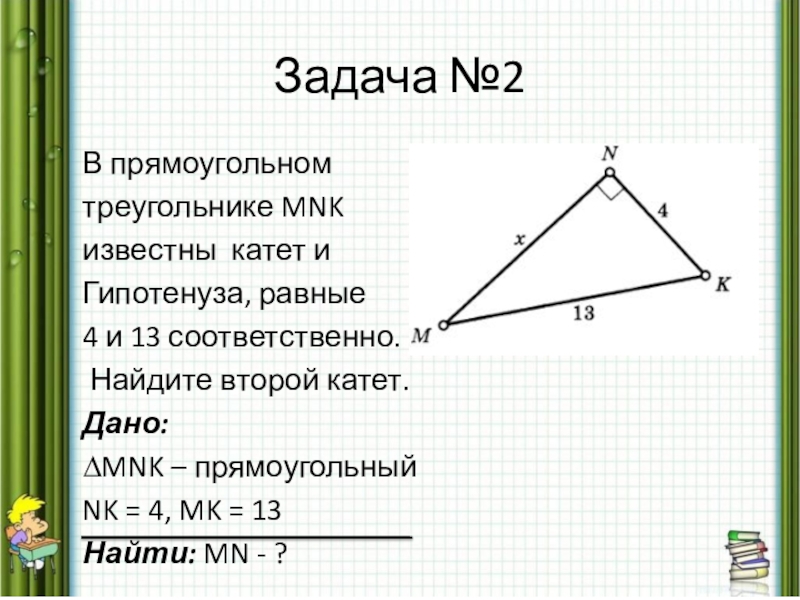
Слайд 16Задача №2
В прямоугольном
треугольнике MNK
известны катет и
Гипотенуза, равные
4 и 13 соответственно.
Найдите второй катет.
Дано:
∆MNK – прямоугольный
NK = 4, MK = 13
Найти: MN - ?
Слайд 18Задача №3
Найдите x:
Дано:
∆RKL – прямоугольный,
равнобедренный;
RK, KL – катеты;
RK = KL =
Найти: RL - ?
Слайд 20Задача № 4
Найдите х:
Дано:
∆MSN – прямоугольный;
NMS = ;
MS, SN – катеты;
MN =
Найти: MS - ?
MS, SN – катеты;
MN =
Найти: MS - ?
Слайд 21Задача № 4
Найдем NS:
NS =
(по
свойству катета,
лежащего против
угла в ).
По теореме Пифагора найдем катет MS:
свойству катета,
лежащего против
угла в ).
По теореме Пифагора найдем катет MS:
Ответ: 3
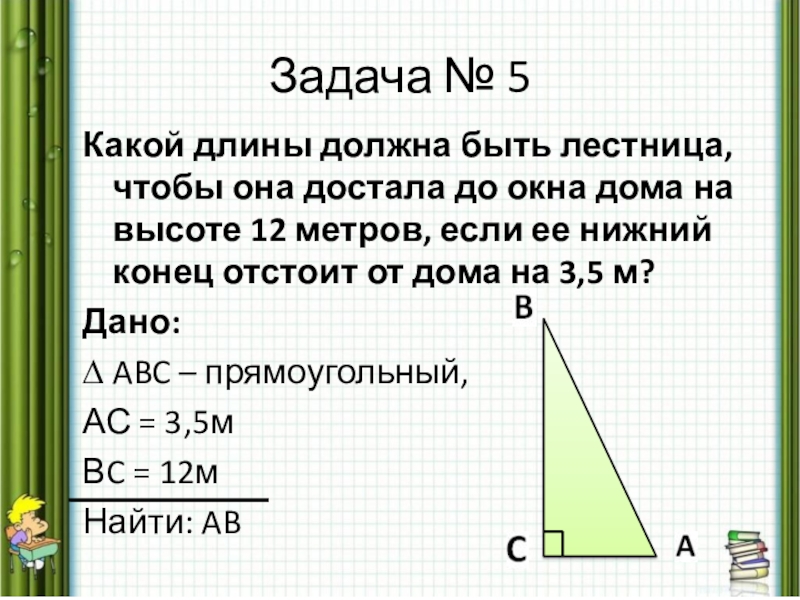
Слайд 22Задача № 5
Какой длины должна быть лестница, чтобы она достала до
окна дома на высоте 12 метров, если ее нижний конец отстоит от дома на 3,5 м?
Дано:
∆ ABC – прямоугольный,
АС = 3,5м
ВC = 12м
Найти: AB
Дано:
∆ ABC – прямоугольный,
АС = 3,5м
ВC = 12м
Найти: AB
Слайд 24Домашнее задание
Знать формулировку и доказательство теоремы Пифагора. Доказать теорему Пифагора
другим способом (по желанию).
Учебник: п. 63, стр.94 № 2(1), № 3 (2,3)
Задача* на доп.отметку (по желанию)
В 32 м. одна от другой растут две сосны. Высота одной 37 м, а другой – 13 м. Найдите расстояние (в метрах) между их верхушками.
Учебник: п. 63, стр.94 № 2(1), № 3 (2,3)
Задача* на доп.отметку (по желанию)
В 32 м. одна от другой растут две сосны. Высота одной 37 м, а другой – 13 м. Найдите расстояние (в метрах) между их верхушками.