- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок геометрии в 7 классе по теме АКСИОМЫ
Содержание
- 1. Урок геометрии в 7 классе по теме АКСИОМЫ
- 2. Великий французский архитектор Ле Корбюзье в
- 3. Формируемые результатыПредметные : сформировать представление учащихся о
- 4. Контроль и коррекция знаний№ 1 Проведите прямую
- 5. Контроль и коррекция знаний№ 2 На рисунке
- 6. ИзучениеновогоматериалаИзучениеновогоматериала
- 7. Аксиома – греческое слово, означает «достоинство», «уважение»,
- 8. Вспомните и назовите те утверждения, которые были приняты без доказательства
- 9. Аксиомы геометрииЧерез любые две точки можно провести
- 10. Но помимо аксиом в геометрии
- 11. Как устроена теоремаРассмотрим следующее утверждение: «если ученик
- 12. Теорема 1.1Теорема 4.1Основное свойство прямойОсновное свойство величины
Великий французский архитектор Ле Корбюзье в начале XX века сказал: «Никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия».
Слайд 2
Великий французский архитектор Ле Корбюзье в начале XX века сказал:
«Никогда до настоящего времени
мы не жили в такой геометрический период. Все вокруг – геометрия».
Слайд 3Формируемые результаты
Предметные : сформировать представление учащихся о роли аксиом при построении
системы геометрических знаний, разъяснить, что с помощью одних свойств фигуры можно доказывать другие свойства.
Личностные : формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
Метапредметные: формировать первоначальные представления об идеях и о методах геометрии как об универсальном языке науки и техники.
Личностные : формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
Метапредметные: формировать первоначальные представления об идеях и о методах геометрии как об универсальном языке науки и техники.
Слайд 4Контроль и коррекция знаний
№ 1
Проведите прямую d и отметьте точку
К, не принадлежащую ей. С помощью угольника проведите через точку К прямую, перпендикулярную прямой d.
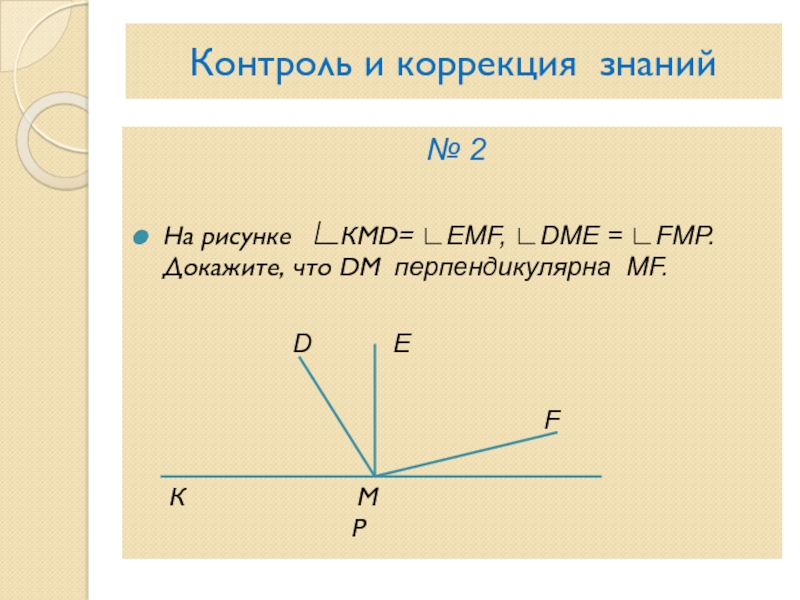
Слайд 5Контроль и коррекция знаний
№ 2
На рисунке ∟КМD= ∟ЕМF, ∟DМЕ
= ∟FМР. Докажите, что DМ перпендикулярна МF.
D Е
F
D Е
F
К
М Р
Слайд 7Аксиома – греческое слово, означает «достоинство», «уважение», «авторитет».
Первоначально имело смысл
«самоочевидная истина».
Термин впервые встречается у Аристотеля, и перешел в
математику от философов
Древней Греции.
Термин впервые встречается у Аристотеля, и перешел в
математику от философов
Древней Греции.
Слайд 9Аксиомы геометрии
Через любые две точки можно провести прямую и притом только
одну.
Из трех точек на прямой одна и только одна лежит между двумя другими.
На любом луче от его начала можно отложить отрезок равный данному и при том только один.
От любого луча в заданную сторону можно отложить угол равный данному и притом только один.
Такие утверждения принимаются в геометрии в качестве исходных положений. На их основе доказываются более сложные утверждения, да и вообще строится геометрия. Эти исходные положения называются аксиомами и принимаются без доказательств.
Из трех точек на прямой одна и только одна лежит между двумя другими.
На любом луче от его начала можно отложить отрезок равный данному и при том только один.
От любого луча в заданную сторону можно отложить угол равный данному и притом только один.
Такие утверждения принимаются в геометрии в качестве исходных положений. На их основе доказываются более сложные утверждения, да и вообще строится геометрия. Эти исходные положения называются аксиомами и принимаются без доказательств.
Слайд 10
Но помимо аксиом в геометрии встречаются утверждения, справедливость которых
надо доказывать путем порой длинных логических рассуждений. Такие утверждения называются теоремами, а цепочка рассуждений является доказательством теоремы.
Теорема – греческое слово, означает «зрелище», «представление». В математике греков это слово стало употребляться в смысле «истина, доступная созерцанию». Само греческое слово происходит от слова «рассматриваю», «обдумываю». Как математический термин встречается у Аристотеля.
Теорема – греческое слово, означает «зрелище», «представление». В математике греков это слово стало употребляться в смысле «истина, доступная созерцанию». Само греческое слово происходит от слова «рассматриваю», «обдумываю». Как математический термин встречается у Аристотеля.
Слайд 11Как устроена теорема
Рассмотрим следующее утверждение: «если ученик не сделал домашнее задание,
то учитель его не похвалит».
Это утверждение состоит из двух частей – условия и вывода. Назовите условие того, что учитель не похвалит ученика - ученик не сделал домашнее задание. А какой вывод можно сделать из того, что ученик не приготовил урок? Вывод: учитель не похвалит такого ученика.
Так и в любой теореме – есть условие теоремы и вывод, называемый заключением. Если рассматривать теорему как задачу, то условие – это то, что дано, то, чем можно пользоваться. Заключение же – неизвестный факт, требующий доказательства.
В теореме после слова «если» формулируется условие этой теоремы, а после слова «то» - заключение, т.е. то, что надо доказать.
Если УСЛОВИЕ ______ , то ЗАКЛЮЧЕНИЕ______.
Дано
Доказать
Это утверждение состоит из двух частей – условия и вывода. Назовите условие того, что учитель не похвалит ученика - ученик не сделал домашнее задание. А какой вывод можно сделать из того, что ученик не приготовил урок? Вывод: учитель не похвалит такого ученика.
Так и в любой теореме – есть условие теоремы и вывод, называемый заключением. Если рассматривать теорему как задачу, то условие – это то, что дано, то, чем можно пользоваться. Заключение же – неизвестный факт, требующий доказательства.
В теореме после слова «если» формулируется условие этой теоремы, а после слова «то» - заключение, т.е. то, что надо доказать.
Если УСЛОВИЕ ______ , то ЗАКЛЮЧЕНИЕ______.
Дано
Доказать
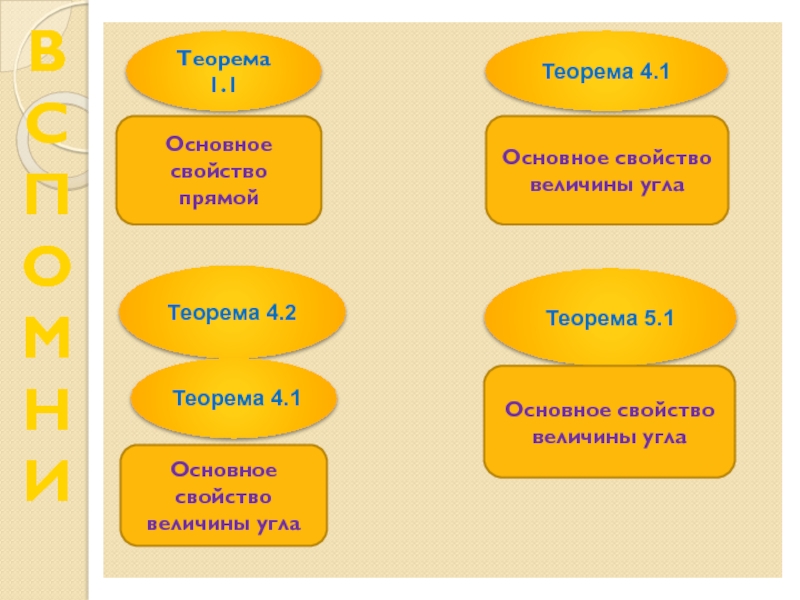
Слайд 12Теорема 1.1
Теорема 4.1
Основное свойство прямой
Основное свойство величины угла
Теорема 4.2
Основное свойство величины
угла
Теорема 4.1
Теорема 5.1
Основное свойство величины угла
ВСПОМНИ