плоскости
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок геометрии 9 класс по теме Движение
Содержание
- 1. Урок геометрии 9 класс по теме Движение
- 2. Отображение плоскости на себя.Любая точка плоскости оказывается сопоставленной некоторой точке.
- 3. Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.
- 4. Понятие движения в геометрии связано с обычным
- 5. Два движения, выполненные последовательно, снова дают движение.
- 6. Параллельный переносОсевая симметрияПоворот вокруг точкиЦентральная симметрия. На плоскости существует четыре типа движений:
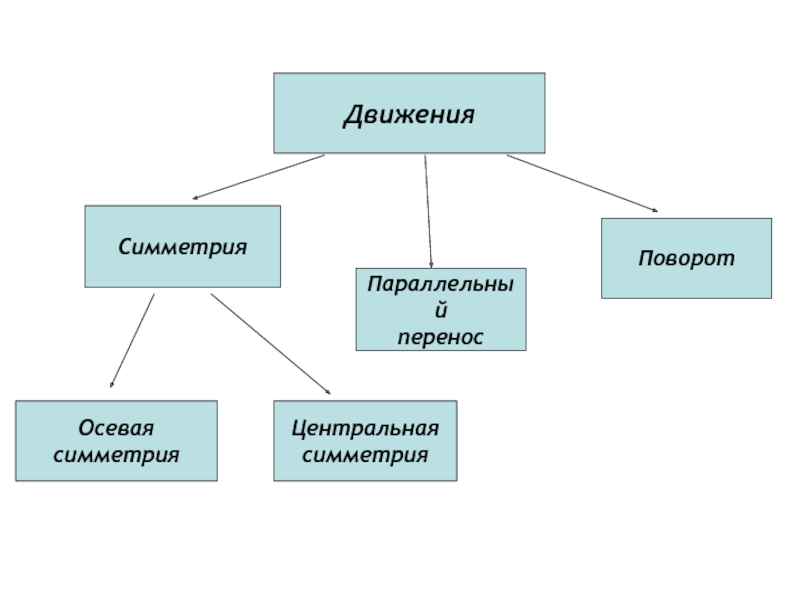
- 7. ДвиженияСимметрияПараллельныйпереносПоворотОсеваясимметрияЦентральнаясимметрия
- 8. Параллельным переносом называется такое движение , при
- 9. Параллельный переносОпределение. Параллельный перенос – это отображение
- 10. ПостроениеПусть дан вектор а. ∆АВС произвольный. От
- 11. Слайд 11
- 12. Слайд 12
- 13. Осевая симметрия — тип симметрии, имеющий два несколько отличающихся определения:Осевая симметрия
- 14. 1) Отражательная симметрия. В математике осевая
- 15. 2) Вращательная симметрия. В естественных
- 16. Осевая симметрия Определение Осевая
- 17. ПостроениеПусть а – ось симметрии.
- 18. Слайд 18
- 19. Слайд 19
- 20. Задача Сколько осей симметрии имеет равносторонний
- 21. С симметрией мы часто встречаемся в быту,архитектуре,технике,природе.
- 22. Поворотом является движение, т.е. отображением
- 23. ПоворотОпределение Поворот плоскости вокруг точки
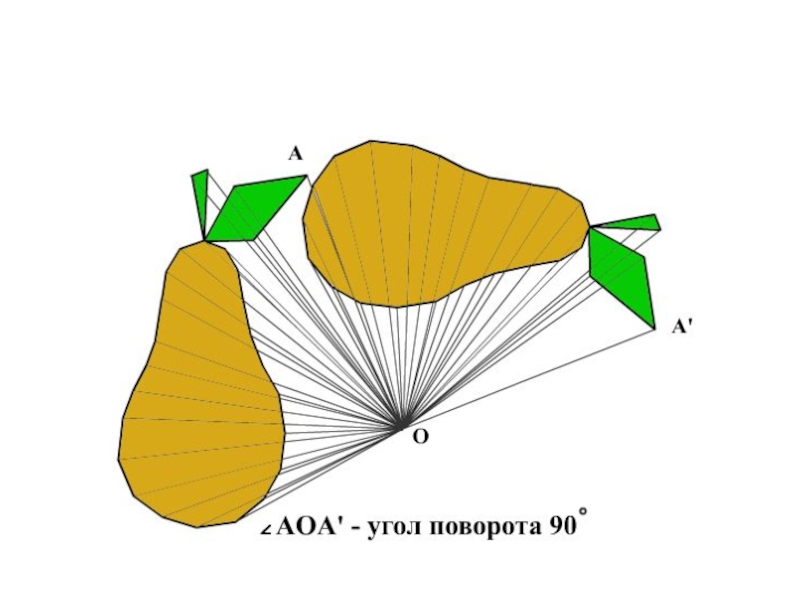
- 24. ПостроениеПусть О – центр поворота, =90º, ∆АВС
- 25. Слайд 25
- 26. Слайд 26
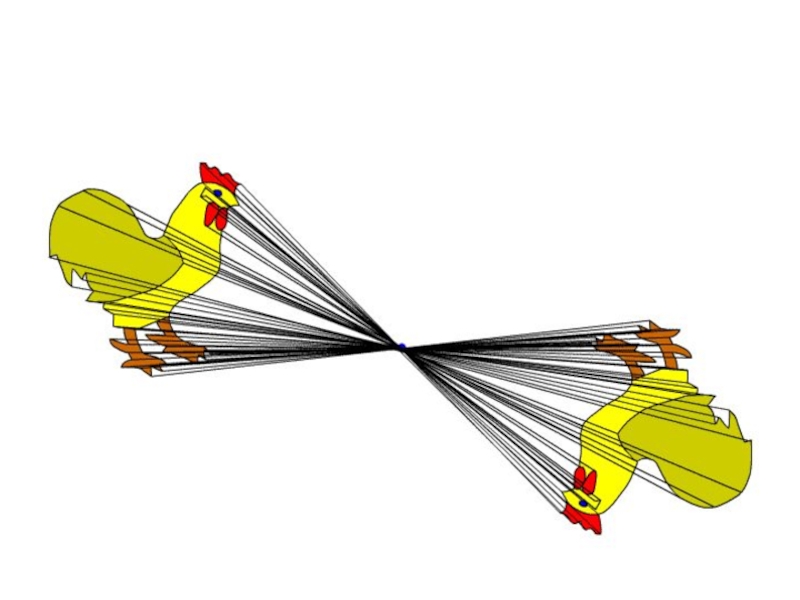
- 27. Центральной симметрий относительно точки A называют
- 28. Центральная симметрияОпределение Центральная симметрия –это отображение
- 29. ПостроениеПусть точка О – центр симметрии. ∆АВС
- 30. Слайд 30
- 31. Слайд 31
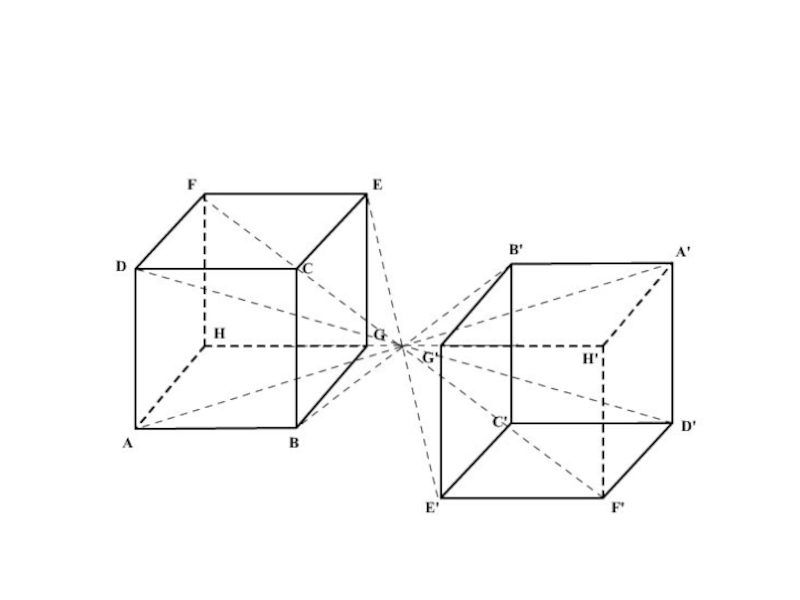
- 32. Пример центральной симметрии
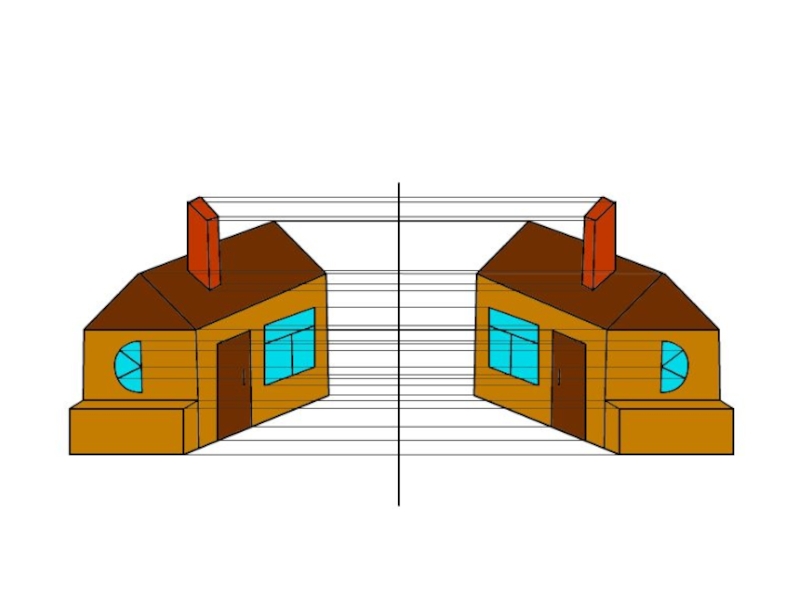
- 33. Движение в архитектуре. Определить вид движения.
- 34. ВопросыОпределить вид симметрии.Что вам приходилось встречать в природе из известных видов симметрии?
- 35. Выполнение практической работыВыполни работу на тот вид движения, который тебе понравился.
- 36. Какие
Отображение плоскости на себя.Любая точка плоскости оказывается сопоставленной некоторой точке.
Слайд 1Тема:
Презентацию выполнили
ученицы 9 «В» класса
школы №56
Зиновьева Елена и Ермолаева Регина
Движение
Слайд 2Отображение плоскости на себя.
Любая точка плоскости оказывается
сопоставленной некоторой точке.
Слайд 4
Понятие движения в геометрии связано с обычным представлением
о перемещении. Но, если
говоря о перемещении, мы представляем себе
непрерывный процесс, то в геометрии для нас будут иметь значение
только начальное и конечное положения фигур.
Слайд 6Параллельный перенос
Осевая симметрия
Поворот вокруг точки
Центральная симметрия.
На плоскости существует четыре типа
движений:
Слайд 8Параллельным переносом называется такое движение , при котором все точки плоскости
перемещаются в одном и том же направлении на одинаковое расстояние.
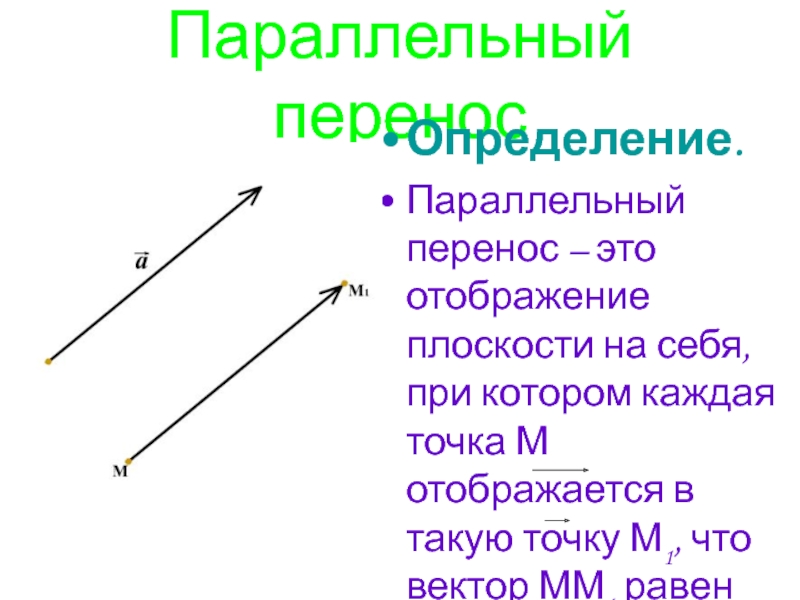
Слайд 9Параллельный перенос
Определение.
Параллельный перенос – это отображение плоскости на себя, при
котором каждая точка М отображается в такую точку М1, что вектор ММ1 равен вектору а.
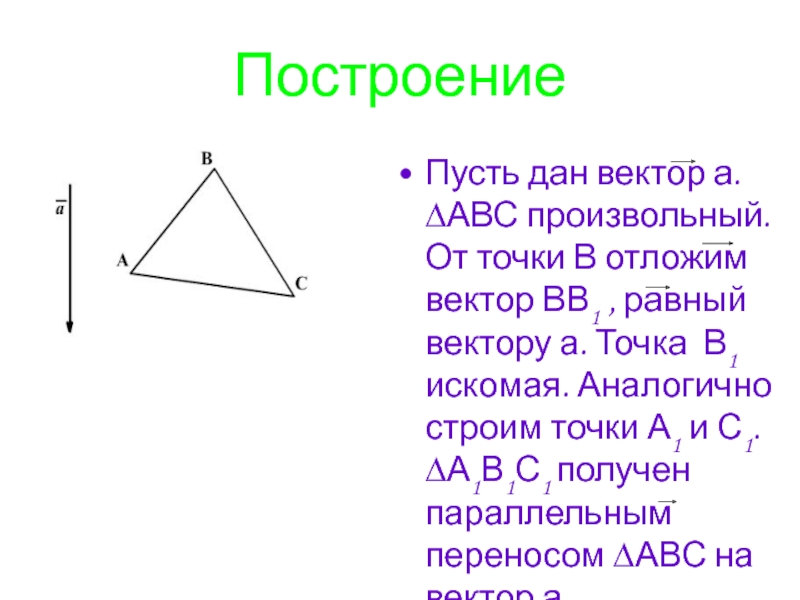
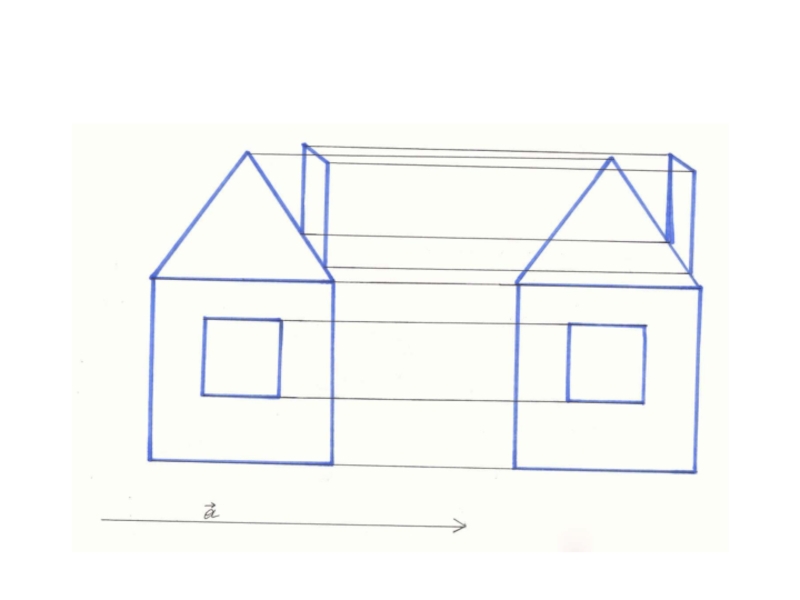
Слайд 10Построение
Пусть дан вектор а. ∆АВС произвольный. От точки В отложим вектор
ВВ1 , равный вектору а. Точка В1 искомая. Аналогично строим точки А1 и С1. ∆А1В1С1 получен параллельным переносом ∆АВС на вектор а.
Слайд 13
Осевая симметрия — тип симметрии, имеющий два несколько отличающихся определения:
Осевая симметрия
Слайд 14
1) Отражательная симметрия. В математике осевая симметрия — вид движения
(зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии
Осевая симметрия
Слайд 15
2) Вращательная симметрия. В естественных науках под осевой симметрией
понимают вращательную симметрию относительно поворотов вокруг прямой.
Осевая симметрия
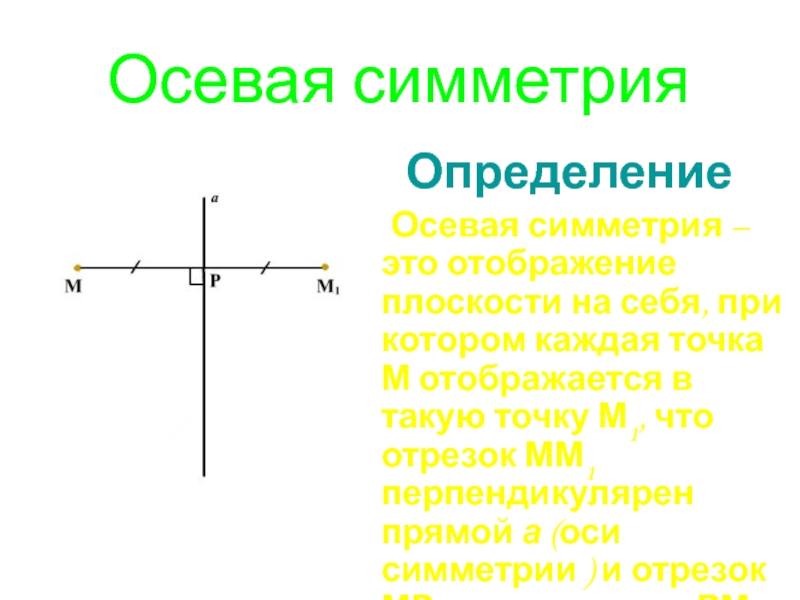
Слайд 16Осевая симметрия
Определение
Осевая симметрия –это отображение плоскости
на себя, при котором каждая точка М отображается в такую точку М1, что отрезок ММ1 перпендикулярен прямой а (оси симметрии ) и отрезок МР равен отрезку РМ1.
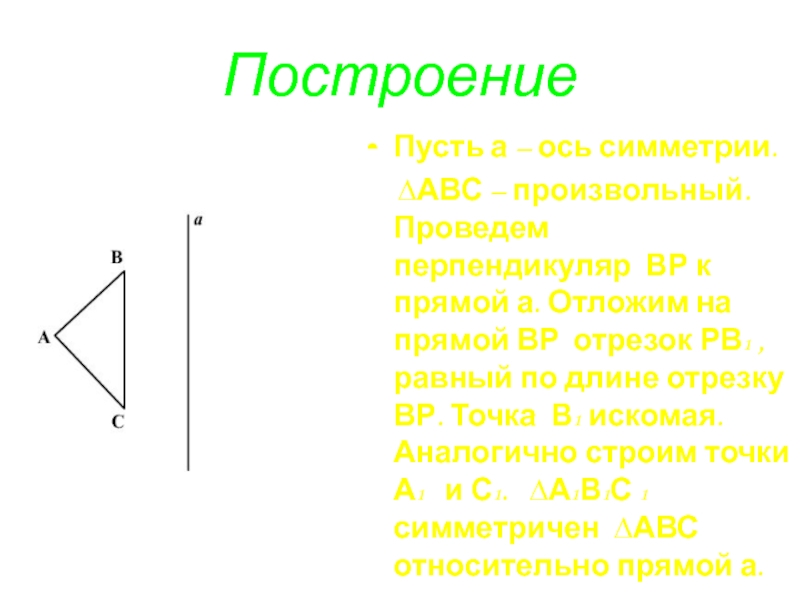
Слайд 17Построение
Пусть а – ось симметрии.
∆АВС – произвольный. Проведем
перпендикуляр ВР к прямой а. Отложим на прямой ВР отрезок РВ1 , равный по длине отрезку ВР. Точка В1 искомая. Аналогично строим точки А1 и С1. ∆А1В1С 1 симметричен ∆АВС относительно прямой а.
Слайд 20Задача
Сколько осей симметрии имеет равносторонний треугольник?
(1 ряд)
Сколько осей симметрии имеет квадрат? (2 ряд)
Сколько осей симметрии имеет ромб, не являющийся квадратом?
(вместе)
Начертите и убедитесь в правильности своего ответа
Слайд 22 Поворотом является движение, т.е. отображением плоскости на себя, сохраняющим
расстояниям.
Поворот вокруг точки
м
N
a
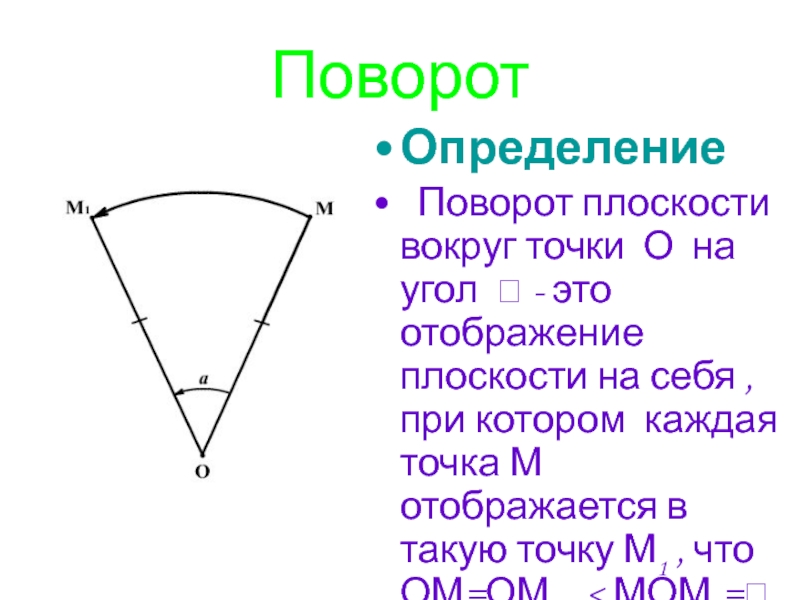
Слайд 23Поворот
Определение
Поворот плоскости вокруг точки О на угол
- это отображение плоскости на себя , при котором каждая точка М отображается в такую точку М1 , что ОМ=ОМ1 , < МОМ1=.
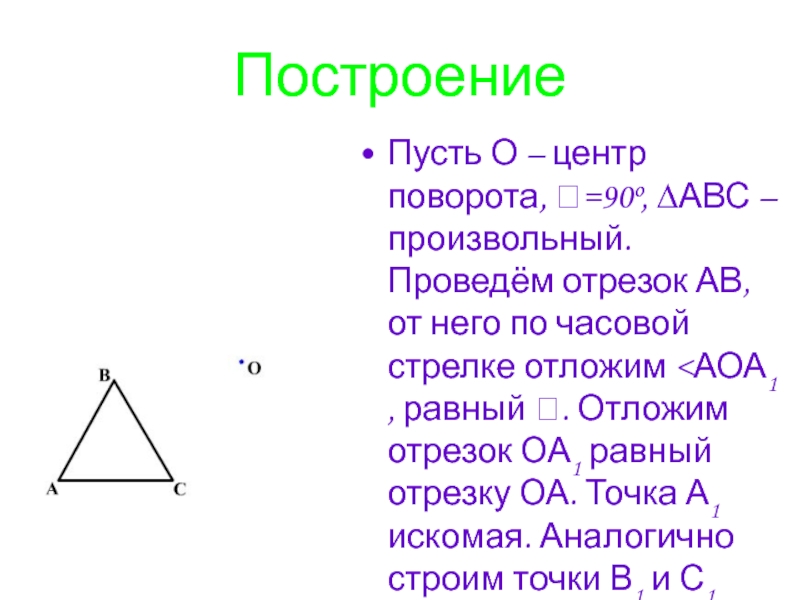
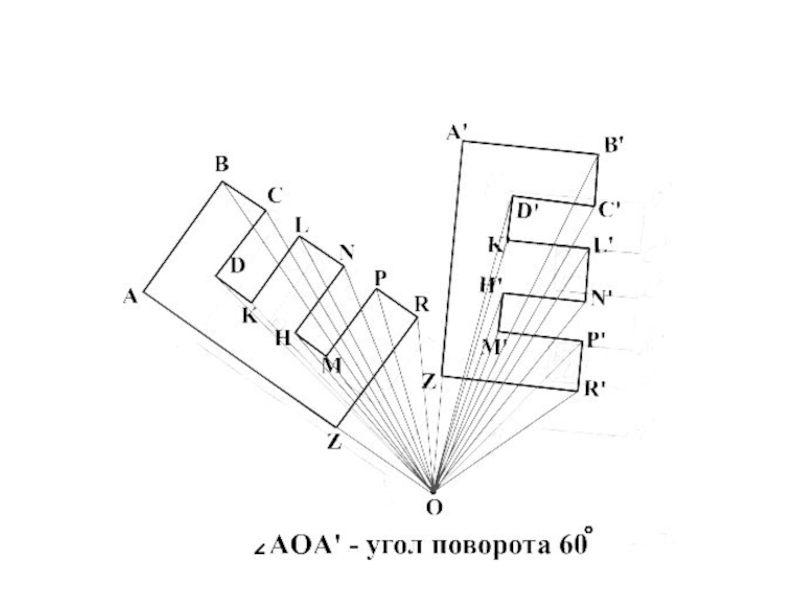
Слайд 24Построение
Пусть О – центр поворота, =90º, ∆АВС – произвольный. Проведём отрезок
АВ, от него по часовой стрелке отложим <АОА1 , равный . Отложим отрезок ОА1 равный отрезку ОА. Точка А1 искомая. Аналогично строим точки В1 и С1
Слайд 27 Центральной симметрий относительно точки A называют преобразование пространства, переводящее точку
X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через Zа, в то время как обозначение Sа можно перепутать с осевой симметрией.
Центральная симметрия
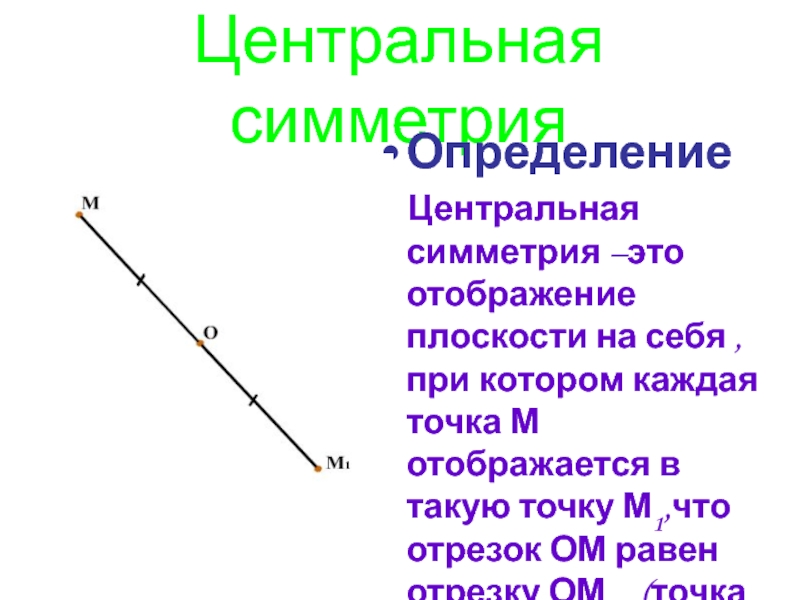
Слайд 28Центральная симметрия
Определение
Центральная симметрия –это отображение плоскости на себя ,
при котором каждая точка М отображается в такую точку М1,что отрезок ОМ равен отрезку ОМ 1 (точка О - центр симметрии).
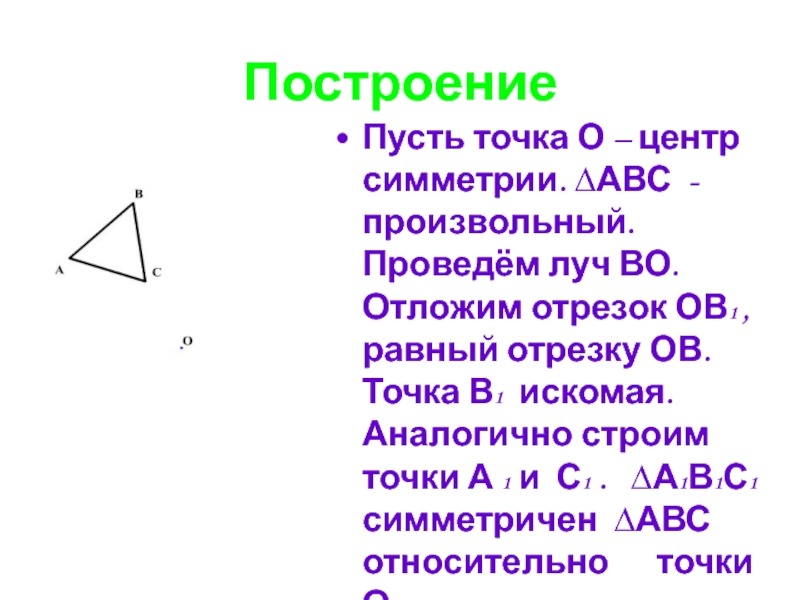
Слайд 29Построение
Пусть точка О – центр симметрии. ∆АВС -произвольный. Проведём луч ВО.
Отложим отрезок ОВ1 , равный отрезку ОВ. Точка В1 искомая. Аналогично строим точки А 1 и С1 . ∆А1В1С1 симметричен ∆АВС относительно точки О.
Слайд 34Вопросы
Определить вид симметрии.
Что вам приходилось встречать в природе из известных видов
симметрии?
Слайд 36
Какие виды движения мы встречаем
с вами в нашей повседневной жизни?
Привлекла ли вас красота симметрии, поворота и движения в архитектуре?
Привлекла ли вас красота симметрии, поворота и движения в архитектуре?