- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Четвёртый признак равенства треугольников
Содержание
- 1. Презентация по геометрии Четвёртый признак равенства треугольников
- 2. Точки А, В и С – вершины
- 3. Два треугольника называются равными, если их можно
- 4. Треугольник состоит из 6 элементов. Трёх углов
- 5. Из курса геометрии 7 класс всем известно,
- 6. В данном случае невозможно утверждать, что треугольники равны. Значит, теорема не верна.
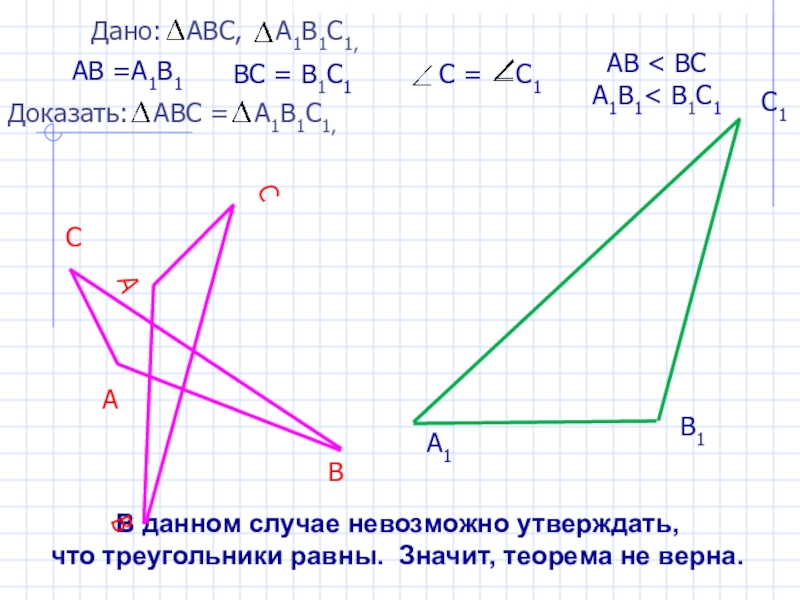
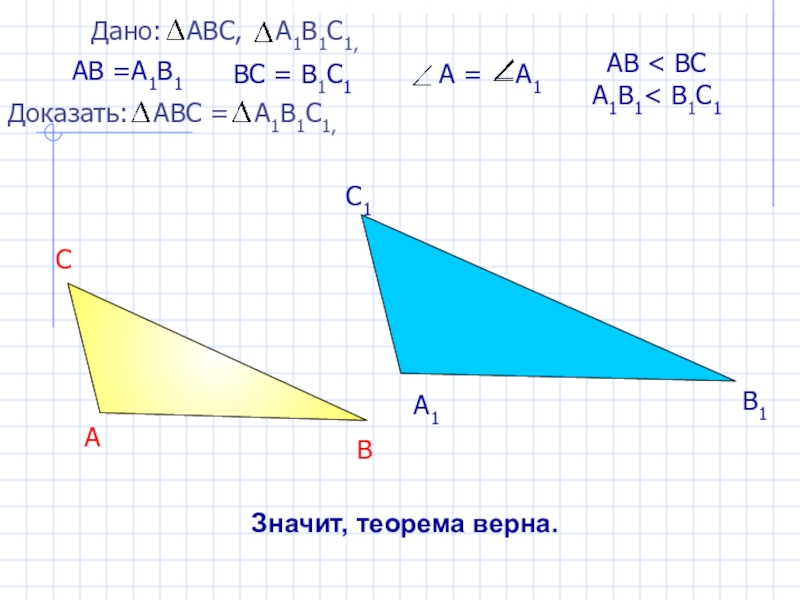
- 7. АВ =А1В1 ВС = В1С1С1А1В1В
- 8. АВ =А1В1 ВС = В1С1С1А1В1 Значит, теорема верна.АВ < BC А1В1< В1С1
- 9. АВ =А1В1 Значит, теорема не
- 10. Вывод: В ходе исследования мы обнаружили ещё
Слайд 1Признаки равенства треугольников
Выполнила Шашкина Софья,
ученица 7А класса
Руководитель Лямцева Ольга Яковлевна
Слайд 2
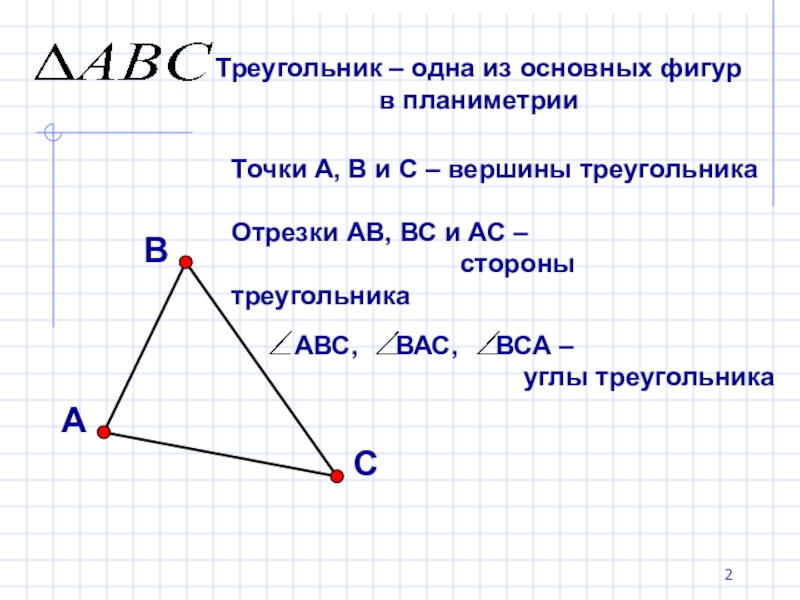
Точки А, В и С – вершины треугольника
Отрезки АВ, ВС и
стороны треугольника
Треугольник – одна из основных фигур в планиметрии
Слайд 3
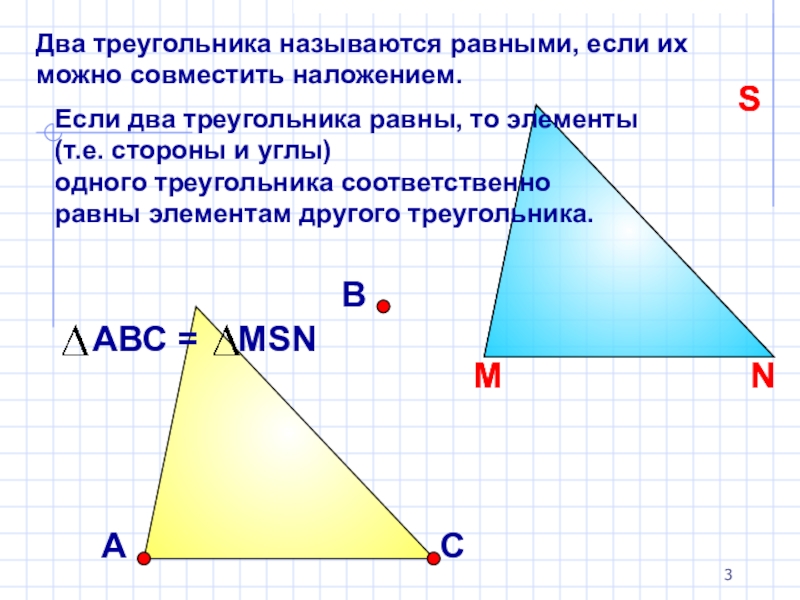
Два треугольника называются равными, если их можно совместить наложением.
Если два треугольника
одного треугольника соответственно равны элементам другого треугольника.
Слайд 4Треугольник состоит из 6 элементов.
Трёх углов и трёх сторон.
Возникает вопрос:
«Какое наименьшее количество элементов нужно взять для установления равенства двух треугольников?»
Слайд 5Из курса геометрии 7 класс всем известно,
что для установления равенства
достаточно использовать три элемента
Возможны следующие тройки элементов:
1. Если две стороны угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
4. Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники равны.
5. Если две стороны и угол лежащий не между ними одного треугольника соответственно равны двум сторонам и углу лежащему не между ними другого треугольника, то такие треугольники равны.
6. Если сторона и два угла не содержащие её одного треугольника соответственно равны стороне и двум углам не содержащим её другого треугольника, то такие треугольники равны
Первым трём соответствуют признаки равенства треугольников, которые учащиеся традиционно изучают в седьмом классе, а вот остальные следует проверить.
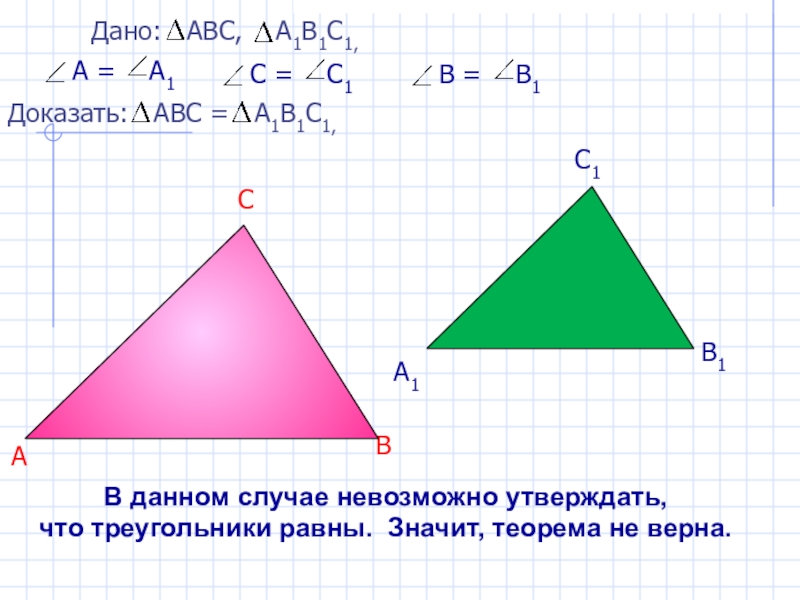
Слайд 7 АВ =А1В1
ВС = В1С1
С1
А1
В1
В данном случае невозможно утверждать,
что треугольники равны. Значит, теорема не верна.
АВ < BC А1В1< В1С1
Слайд 9 АВ =А1В1
Значит, теорема не верна.
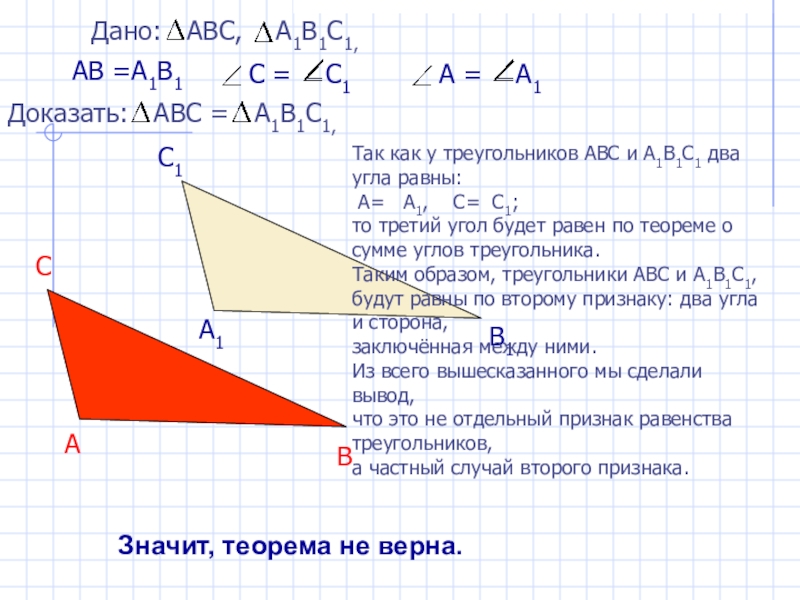
Так как у треугольников
А= А1, С= С1;
то третий угол будет равен по теореме о сумме углов треугольника.
Таким образом, треугольники АВС и А1В1С1,
будут равны по второму признаку: два угла и сторона,
заключённая между ними.
Из всего вышесказанного мы сделали вывод,
что это не отдельный признак равенства треугольников,
а частный случай второго признака.
Слайд 10
Вывод:
В ходе исследования мы обнаружили ещё один признак равенства треугольников.
