пространстве
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Симметрия в пространстве
Содержание
- 1. Презентация по геометрии Симметрия в пространстве
- 2. Геометрический объект называется симметричным, если после того
- 3. Преобразование, переводящее каждую точку А фигуры в
- 4. Слайд 4
- 5. Зеркальной симметрией фигуры относительно плоскости называется отображение,
- 6. Фигура называется симметричной относительно прямой А, если
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
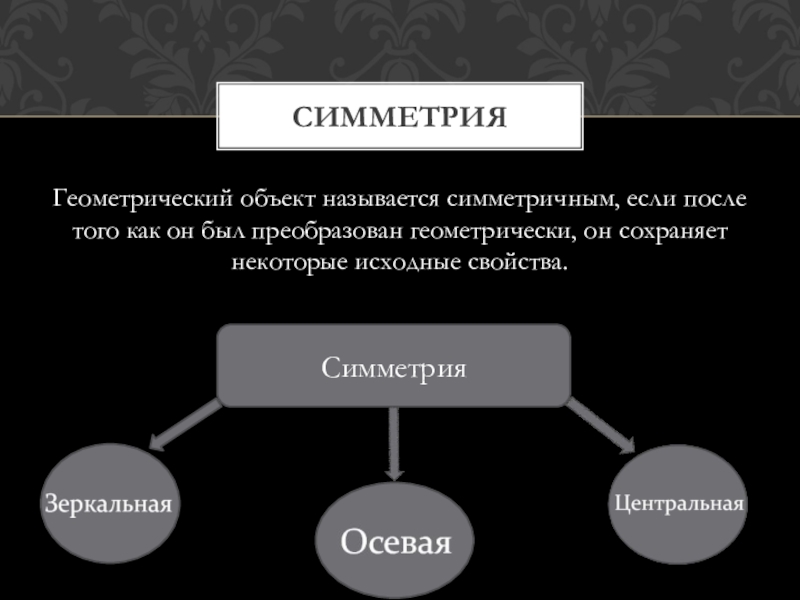
Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. СимметрияСимметрия
Слайд 2Геометрический объект называется симметричным, если после того как он был преобразован
геометрически, он сохраняет некоторые исходные свойства.
Симметрия
Симметрия
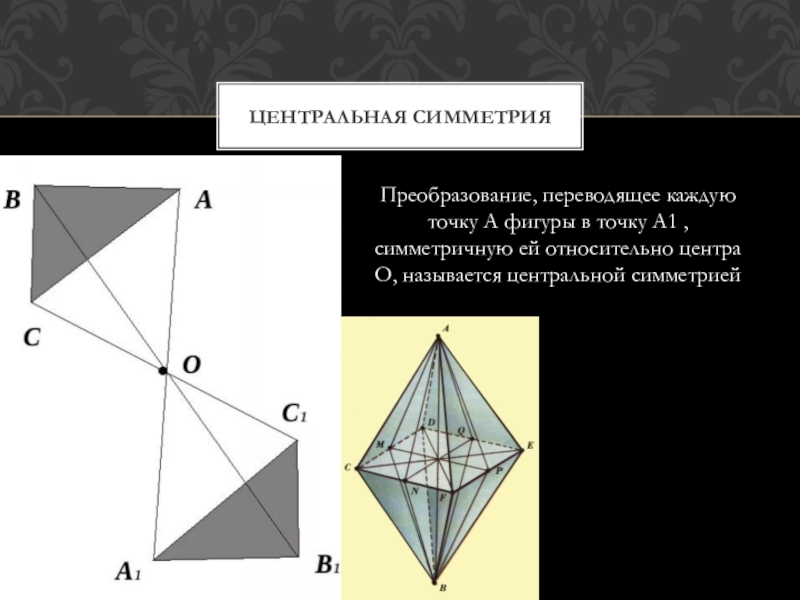
Слайд 3Преобразование, переводящее каждую точку А фигуры в точку А1 , симметричную
ей относительно центра О, называется центральной симметрией
Центральная симметрия
Слайд 5Зеркальной симметрией фигуры относительно плоскости называется отображение, при котором получается фигура,
составленная из точек, симметричных относительно этой плоскости каждой точке начальной фигуры.
Зеркальная симметрия
Слайд 6Фигура называется симметричной относительно прямой А, если для каждой точки фигуры
симметричная ей точка относительно прямой А также принадлежит этой фигуре.
Осевая симметрия