- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Уравнения в геометрических задачах
Содержание
- 1. Уравнения в геометрических задачах
- 2. Линейные уравнения
- 3. №5. (Фольклор). В равнобедренном треугольнике АВС (АВ
- 4. Слайд 4
- 5. Квадратные уравнения
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
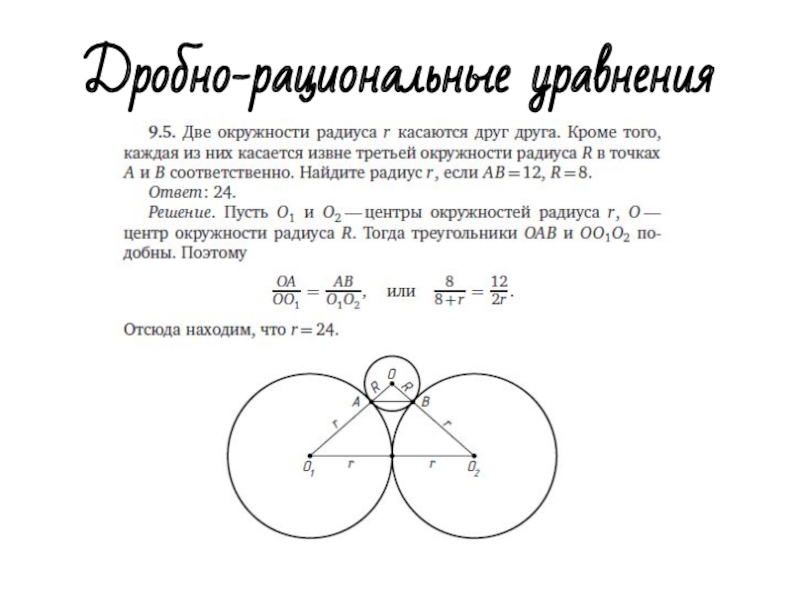
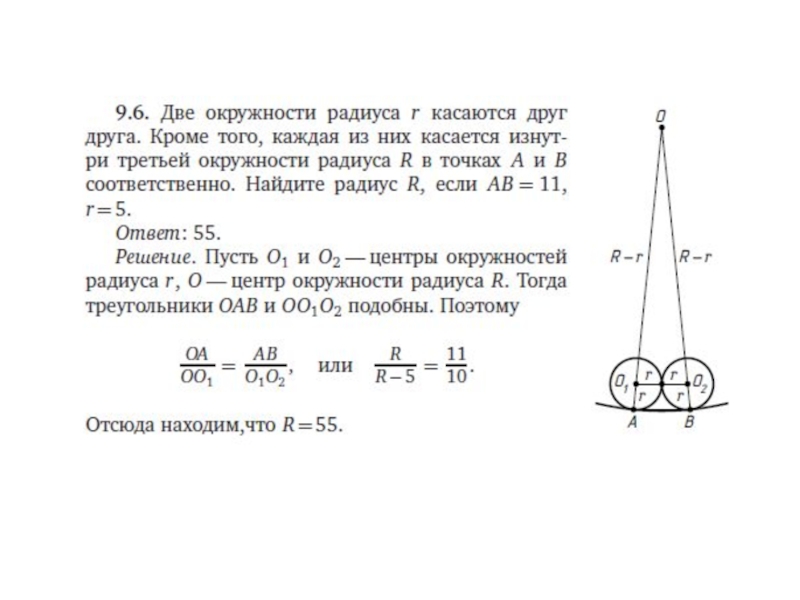
- 13. Дробно-рациональные уравнения
- 14. Слайд 14
- 15. Слайд 15
- 16. Тригонометрические уравнения
- 17. Слайд 17
- 18. Слайд 18
- 19. Системы уравнений
- 20. Слайд 20
- 21. В равнобедренном треугольнике основание
- 22. Однородные уравнения
- 23. Слайд 23
- 24. Уравнения высших степеней
- 25. Слайд 25
- 26. «Не смотря на то что эстетически геометрические
- 27. Использованная литература
Слайд 1Уравнения в геометрических задачах
подготовила
МОУ СШ №57 г. Волгограда
Фомина Е.М.
Слайд 3
№5. (Фольклор). В равнобедренном треугольнике АВС (АВ = АС) провели биссектрису
Ответ: 100.
Решение. Отметим на стороне ВС точку K так, чтобы BK = BD, тогда CK = AD.
Пусть АВD = CВD = , тогда АCВ = 2. Проведем DP || BC.
Так как РDВ = DВС = , то треугольник BPD – равнобедренный (BP = PD).
Треугольник АРD – также равнобедренный с углом 2 при основании РD.
Учитывая, что ВР = CD получим равенство треугольников АРD и KDC (AD = KC, РD = DC, АDP = KCD).
Следовательно, треугольник KDC – равнобедренный и CDK = 2.
Значит, в равнобедренном треугольнике BDK угол при основании равен 4.
Используя для этого треугольника теорему о сумме углов, получим: + 4 + 4 = 180, откуда = 20.
Следовательно, ВАС = 180 – 4 = 100.
Слайд 21 В равнобедренном треугольнике основание равно 10 см, а
Решение:
Ответ: R= см.
Найдите основание равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию, в отношении 12:5, считая от вершины, а боковая сторона равна 60 см.
Решение:
Ответ: АС = 5дм.
Слайд 26 «Не смотря на то что эстетически геометрические методы выглядят гораздо привлекательнее
И.Ф. Шарыгин