.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Углы и отрезки связанные с окружностью
Содержание
- 1. Углы и отрезки связанные с окружностью
- 2. Актуальность Уже очень скоро учащимся
- 3. Цель: систематизировать и обобщить основные формулы, определения
- 4. Предмет исследования: окружностьОбъект исследования: углы и отрезки
- 5. Самая простая из кривых линий – окружность.
- 6. Окружность — множество точек плоскости,
- 7. Основные понятия. Касательная – это прямая,
- 8. Центральный уголВписанный угол
- 9. Центр – данная точка.Радиус – это любой
- 10. Из истории о вписанных углах Изложенное в
- 11. Свойства вписанных углов:Вписанный угол либо равен половине
- 12. Свойства касательной Касательная к окружности перпендикулярна
Актуальность Уже очень скоро учащимся 9-х классов предстоит сдавать Основной государственный экзамен и у некоторых учеников уровень подготовки к этому экзамену находится ниже среднего.
Слайд 2Актуальность
Уже очень скоро учащимся 9-х классов предстоит сдавать
Основной государственный экзамен и у некоторых учеников уровень подготовки к этому экзамену находится ниже среднего.
Слайд 3Цель: систематизировать и обобщить основные формулы, определения связанные с окружностью.
Задачи:
1. Изучить литературу по данной теме.
2. Провести тест среди учащихся моего класса, с целью выяснить, умеют ли ребята решать задачу №17 из сборника по ОГЭ.
3. Сделать информационную брошюру о углах, отрезках связанных с окружностью.
4. Проанализировать полученные знания и оформить результаты исследования.
2. Провести тест среди учащихся моего класса, с целью выяснить, умеют ли ребята решать задачу №17 из сборника по ОГЭ.
3. Сделать информационную брошюру о углах, отрезках связанных с окружностью.
4. Проанализировать полученные знания и оформить результаты исследования.
Слайд 4Предмет исследования: окружность
Объект исследования: углы и отрезки связанные с окружностью.
Методы и
методики решения основных задач:
1. Поиск и сбор информации.
2. Решение теста.
3. Составление сборника по данной теме.
4. Оформление брошюры.
5. Анализ.
Гипотеза:
Мы предположили , что после создания сборника правил,
у учащихся повысится уровень решения задания №17
1. Поиск и сбор информации.
2. Решение теста.
3. Составление сборника по данной теме.
4. Оформление брошюры.
5. Анализ.
Гипотеза:
Мы предположили , что после создания сборника правил,
у учащихся повысится уровень решения задания №17
Слайд 5 Самая простая из кривых линий – окружность. Это одна из древнейших
геометрических фигур. Философы древности придавали ей большое значение.
Еще вавилоняне и древние индийцы считали самым важным элементом окружности – радиус. Слово это латинское и означает «луч». В древности не было этого термина. Евклид и другие ученые говорили просто «прямая из центра». В одной латинской рукописи XI в., названной «Искусство геометрии», встречается впервые термин «полудиаметр».
Еще вавилоняне и древние индийцы считали самым важным элементом окружности – радиус. Слово это латинское и означает «луч». В древности не было этого термина. Евклид и другие ученые говорили просто «прямая из центра». В одной латинской рукописи XI в., названной «Искусство геометрии», встречается впервые термин «полудиаметр».
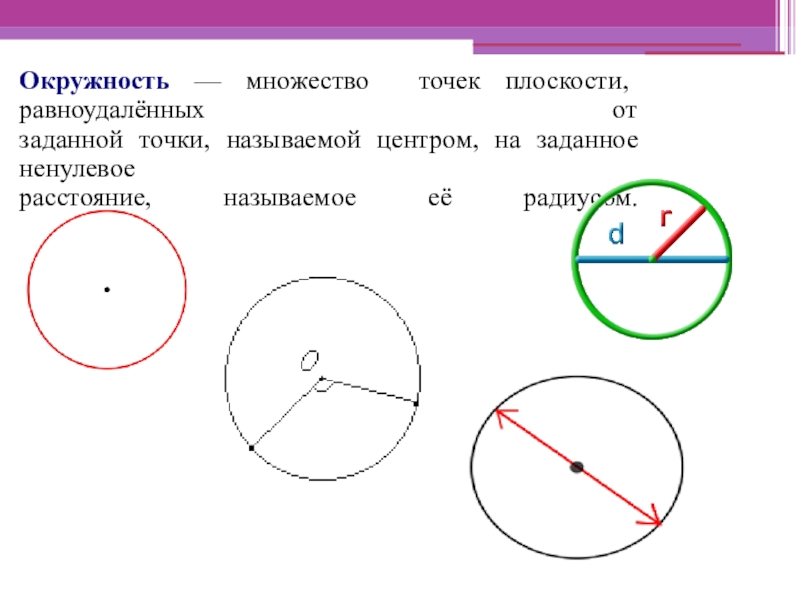
Слайд 6 Окружность — множество точек плоскости, равноудалённых от заданной точки, называемой центром,
на заданное ненулевое
расстояние, называемое её радиусом.
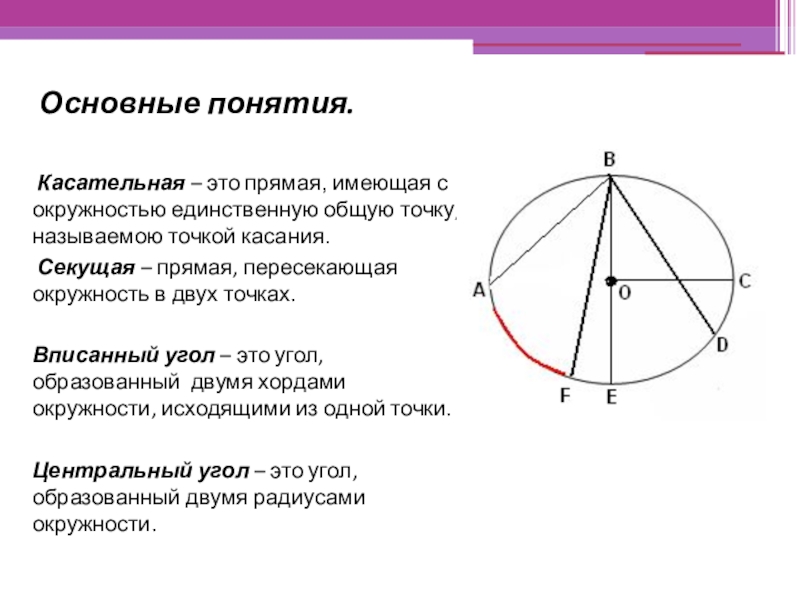
Слайд 7 Основные понятия.
Касательная – это прямая, имеющая с окружностью единственную
общую точку, называемою точкой касания.
Секущая – прямая, пересекающая окружность в двух точках.
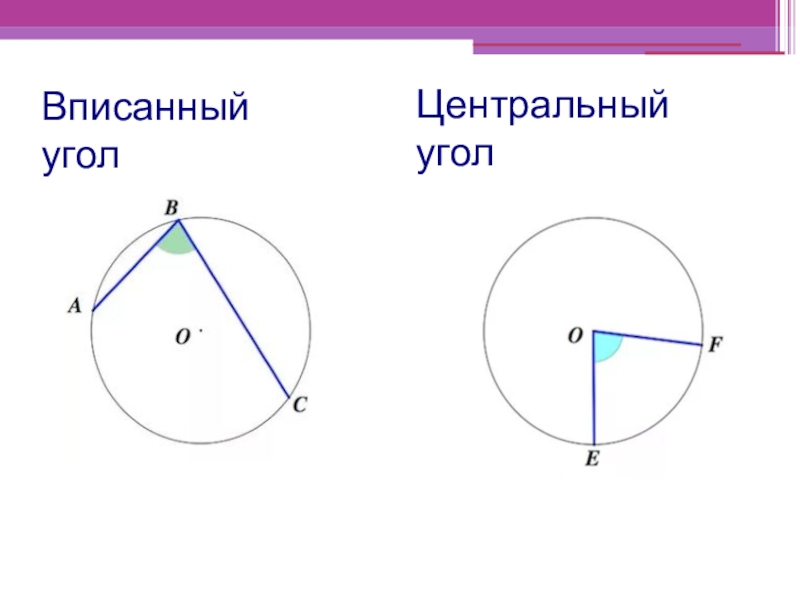
Вписанный угол – это угол, образованный двумя хордами окружности, исходящими из одной точки.
Центральный угол – это угол, образованный двумя радиусами окружности.
Секущая – прямая, пересекающая окружность в двух точках.
Вписанный угол – это угол, образованный двумя хордами окружности, исходящими из одной точки.
Центральный угол – это угол, образованный двумя радиусами окружности.
Слайд 9Центр – данная точка.
Радиус – это любой отрезок, соединяющий центр окружности
и точку окружности.
Хорда – это отрезок, соединяющий две точки окружности.
Диаметр – это хорда проходящая через центр окружности.
Дуга – любая из двух частей окружности, на которые ее делят две лежащие на ней точки.
Хорда – это отрезок, соединяющий две точки окружности.
Диаметр – это хорда проходящая через центр окружности.
Дуга – любая из двух частей окружности, на которые ее делят две лежащие на ней точки.
Слайд 10Из истории о вписанных углах
Изложенное в современных учебниках доказательство того,
что
вписанный угол измеряется половиной дуги,
на которую он опирается, дано в «Началах» Евклида.
На это предложение ссылается, однако,
еще Гиппократ Хиосский (V в. До н. э.) Вписанный угол
был известен вавилонянам еще 4000 лет назад.
на которую он опирается, дано в «Началах» Евклида.
На это предложение ссылается, однако,
еще Гиппократ Хиосский (V в. До н. э.) Вписанный угол
был известен вавилонянам еще 4000 лет назад.
Слайд 11Свойства вписанных углов:
Вписанный угол либо равен половине центрального угла,
опирающегося на его дугу, либо дополняет половину этого угла до 180°.
Вписанный угол, опирающийся на дугу длиной в половину окружности,
всегда прямой (равен 90°).
Вписанный угол не меняет своей величины при перемещении его
вершины вдоль окружности.
Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
Слайд 12
Свойства касательной
Касательная к окружности перпендикулярна радиусу окружности, проведенному
в точку касания.
Если из некоторой точки плоскости проведены две касательные к окружности, то отрезки касательных от этой точки до точек касания равны.
Если из некоторой точки плоскости проведены две касательные к окружности, то прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам.
Если из некоторой точки плоскости проведены две касательные к окружности, то отрезки касательных от этой точки до точек касания равны.
Если из некоторой точки плоскости проведены две касательные к окружности, то прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам.