- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
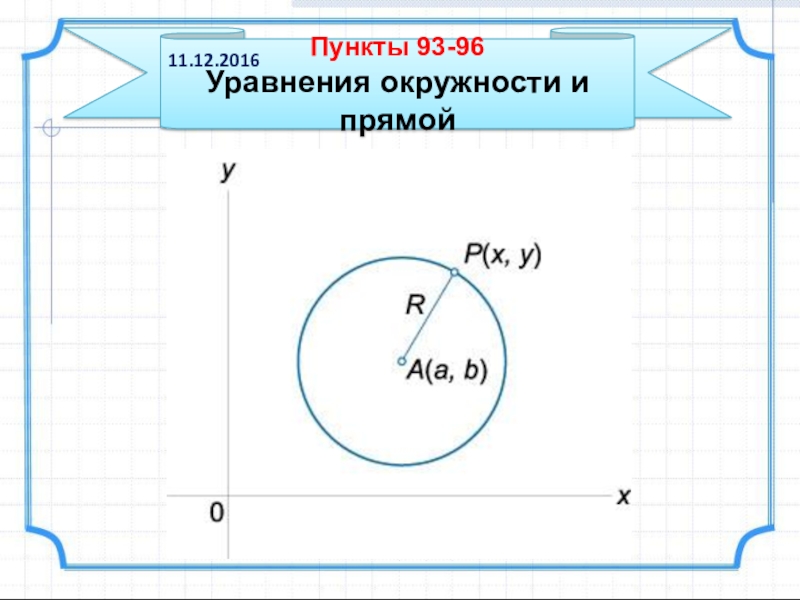
Презентация, доклад на тему Учебная презентация по теме Уравнения окружности и прямой
Содержание
- 1. Учебная презентация по теме Уравнения окружности и прямой
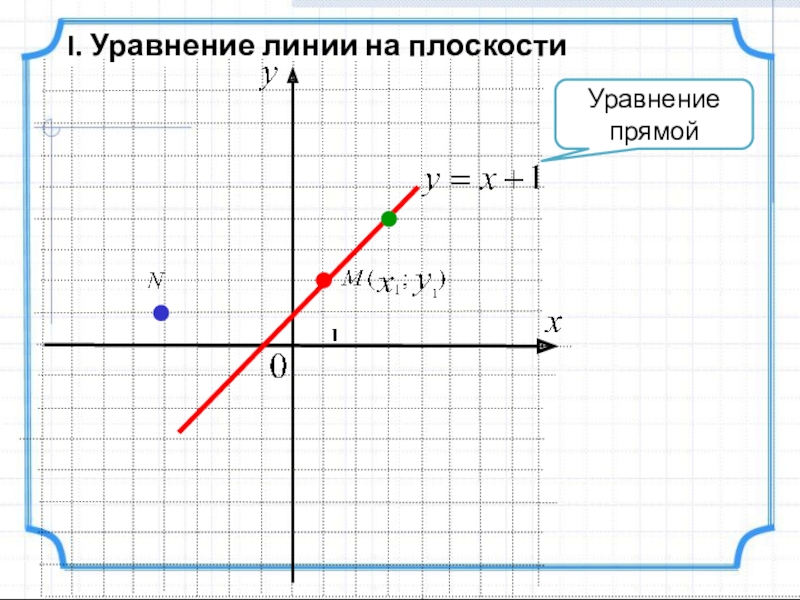
- 2. I. Уравнение линии на плоскостиУравнение прямой
- 3. УХ011хуLУравнение с двумя переменными x и y
- 4. II. Уравнение окружностиОкружность — это фигура, которая состоит
- 5. Задача №1Найти центр и радиусы окружностейC (2;
- 6. Задача №3Начертите окружностьx2 + y2 = 16(x
- 7. Задача №4Написать уравнение окружности С центром в
- 8. Задача №5На окружности, заданной уравнением (x -
- 9. Задача №6Написать уравнение окружности с центром в
- 10. № 1002 (а)Напишите уравнение окружности, проходящей через три данные точки: А(1; -4), В(4; 5), C(3; -2)Ответ:
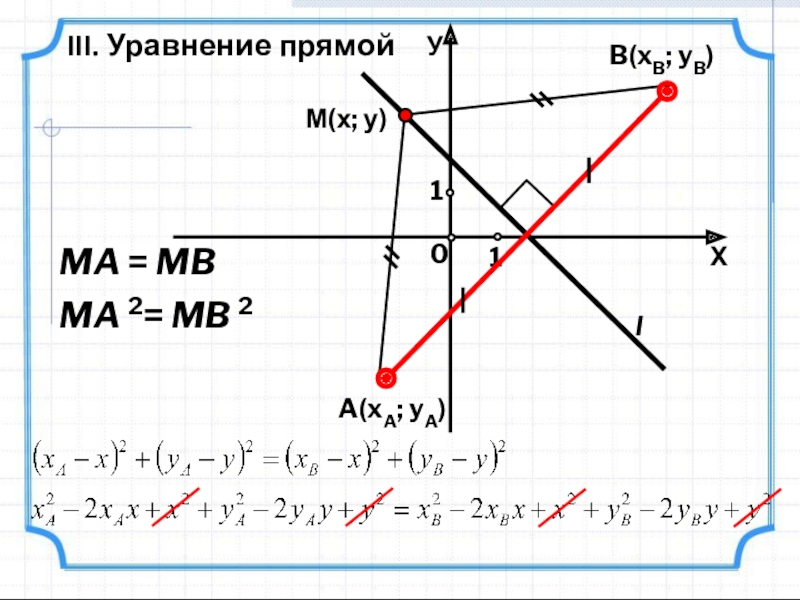
- 11. III. Уравнение прямойA(xA; yA)B(xB; yB)lMA = MBMA 2= MB 2
- 12. Уравнение прямойa и b одновременно не равны
- 13. Угловой коэффициент прямойТеорема о угловом коэффициенте прямойДве
- 14. Задача №7Напишите уравнение прямой, проходящей через точки А (1; -1) и В (-3; 2)
- 15. № 973Даны координаты вершин треугольника ABC: А(4;
- 16. № 975Найдите координаты точек пересечения прямой
- 17. № 976Найдите координаты точки пересечения прямых
- 18. IV. Взаимное расположение двух окружностейРассмотрим две окружности:r,
- 19. 3. R – r < d <
- 20. № 997Докажите, что четырехугольник ABCD, вершины которого
- 21. № 999. Найдите координаты четвёртой вершины параллелограмма
- 22. ABCD – параллелограмм (AB = DC)
- 23. № 980. Напишите уравнения прямых, содержащих стороны
- 24. Дано: ABCD – ромб, AC Ox,
- 25. Дано: ABCD – ромб, AC Ox,
- 26. № 1007. Докажите, что отрезок, соединяющий середины
- 27. Домашнее заданиеП. 93-94, №966, №969(б), №981, 1002(б)П. 95-96, №972(б), №979, №984№990, №1010Подготовиться к КР
Слайд 3У
Х
0
1
1
х
у
L
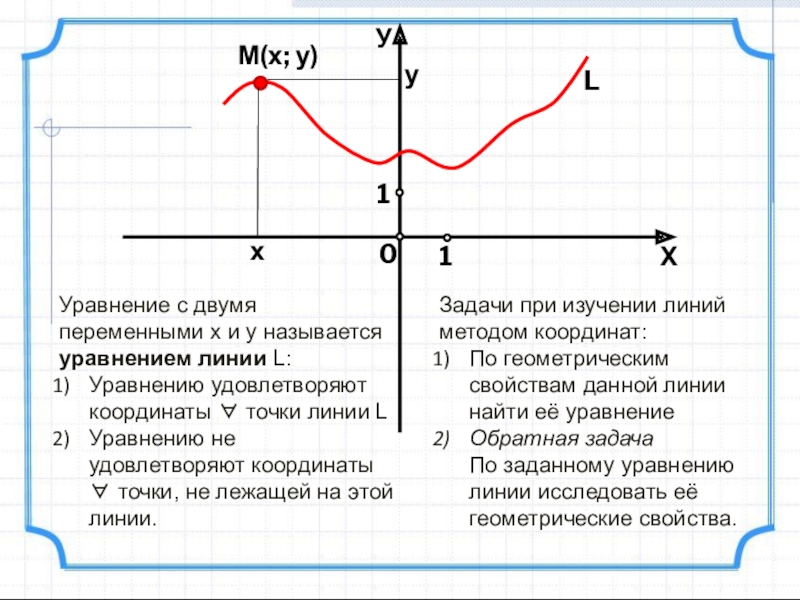
Уравнение с двумя переменными x и y называется уравнением линии L:
Уравнению
Уравнению не удовлетворяют координаты точки, не лежащей на этой линии.
Задачи при изучении линий методом координат:
По геометрическим свойствам данной линии найти её уравнение
Обратная задача
По заданному уравнению линии исследовать её геометрические свойства.
Слайд 4II. Уравнение окружности
Окружность
— это фигура, которая состоит из всех точек на
Окр (C, r)
C (x0; y0)
M Окр
М (x; y)
MC = r
Уравнение окружности
Слайд 5Задача №1
Найти центр и радиусы окружностей
C (2; 7), r =3
C (4;
C (0; 0), r =5
C (9; 0), r =
Задача №2
Выбрать уравнения окружностей
x2 + y2 = 81
4x2 + y2 = 4
(x - 2)2 + (y + 1)2 = 9
x2 + y2 = -1
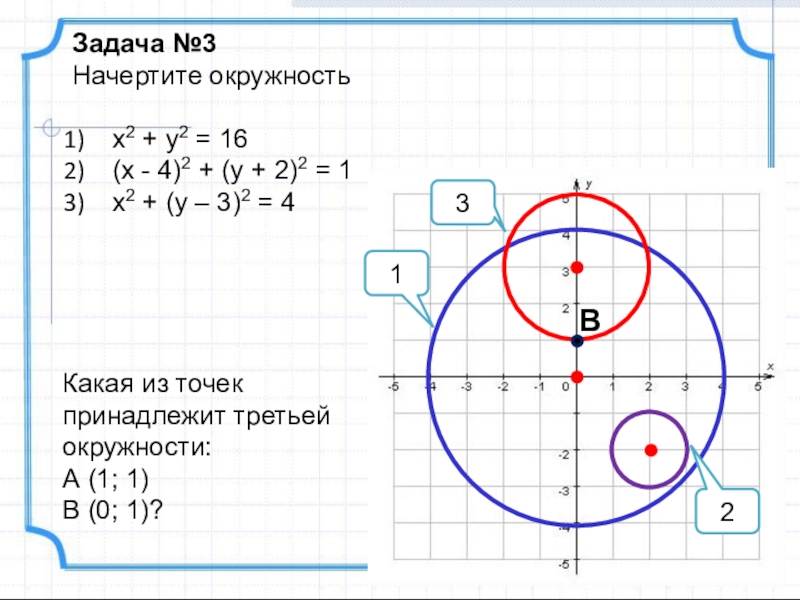
Слайд 6Задача №3
Начертите окружность
x2 + y2 = 16
(x - 4)2 + (y
x2 + (y – 3)2 = 4
2
1
3
Какая из точек принадлежит третьей окружности:
А (1; 1)
В (0; 1)?
В
Слайд 7Задача №4
Написать уравнение окружности
С центром в начале координат и радиуса
С центром в начале координат и радиуса
С центром в точке А(0;5) радиуса 3
С центром в точке А(-1 ; 2) радиуса
Слайд 8Задача №5
На окружности, заданной уравнением
(x - 3)2 + (y -
Найдите точки с абсциссой 3
Найдите точки с ординатой 5
Решение:
x = 3
(y - 5)2 = 25 y1 = 10; y2 = 0
Точки: (3; 10), (3; 0)
Решение:
y = 5
(x - 3)2 = 25 x1 = 8; x2 = -2
Точки: (8; 5), (-2; 5)
Слайд 9Задача №6
Написать уравнение окружности с центром в точке А(-3; 4), проходящей
Написать уравнение окружности с центром в точке А(0; 6), проходящей через точку В(-3; 2)
Написать уравнение окружности с диаметром MN, если M(-3; 5), N(-7; 3)
Слайд 10№ 1002 (а)
Напишите уравнение окружности, проходящей через три данные точки: А(1;
Ответ:
Слайд 12Уравнение прямой
a и b одновременно не равны нулю
Если a =
Если b = 0, то x = c2 – прямая || Oy
Если с = 0, то прямая проходит через O (0; 0)
Ось Ox: y = 0
Ось Oy: x = 0
Слайд 13Угловой коэффициент прямой
Теорема о угловом коэффициенте прямой
Две параллельные прямые, не параллельные
Обратная теорема:
Если две прямые имеют одинаковые угловые коэффициенты, то эти прямые параллельны.
Прямые параллельны
Прямые НЕ параллельны
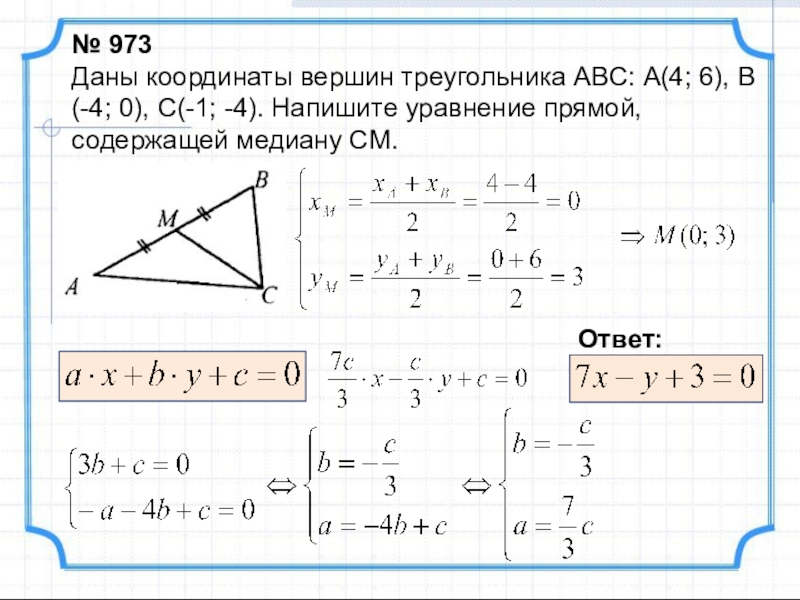
Слайд 15№ 973
Даны координаты вершин треугольника ABC: А(4; 6), В(-4; 0), C(-1;
Ответ:
Слайд 16№ 975
Найдите координаты точек пересечения прямой
3x - 4y + 12=0
Решение:
1) l Ox = A A (x; 0)
3x - 40 + 12=0
x = -4 A (-4; 0)
2) l Oy = B B (0; y)
30 - 4y + 12=0
y = 3 B (0; 3)
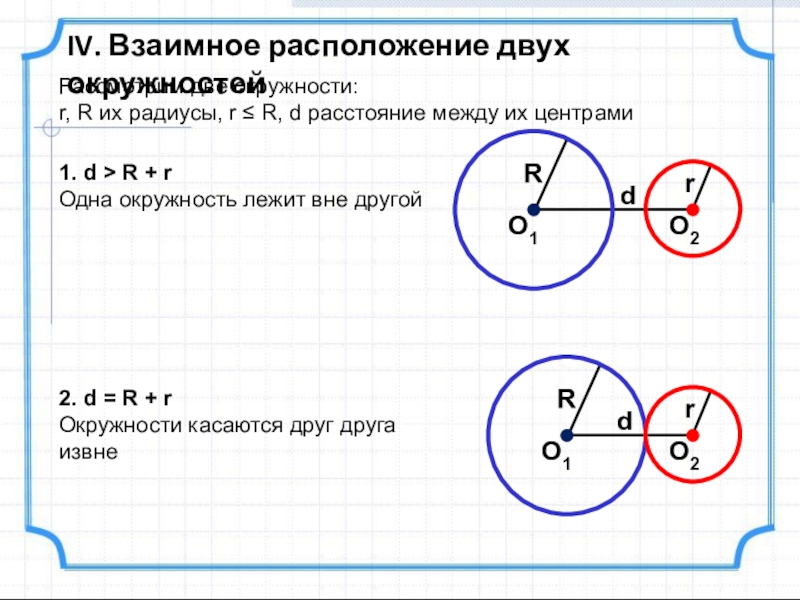
Слайд 18IV. Взаимное расположение двух окружностей
Рассмотрим две окружности:
r, R их радиусы, r
1. d > R + r
Одна окружность лежит вне другой
2. d = R + r
Окружности касаются друг друга извне
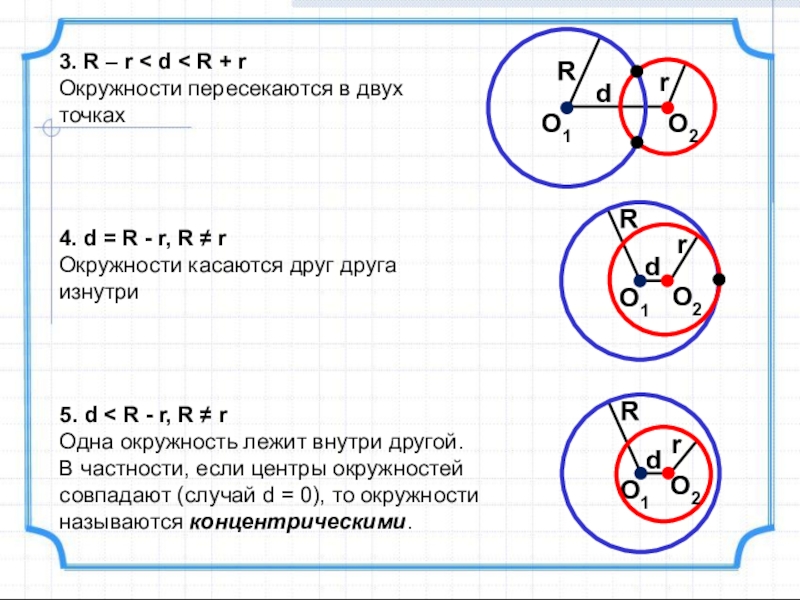
Слайд 193. R – r < d < R + r
Окружности
4. d = R - r, R ≠ r
Окружности касаются друг друга изнутри
5. d < R - r, R ≠ r
Одна окружность лежит внутри другой.
В частности, если центры окружностей совпадают (случай d = 0), то окружности называются концентрическими.
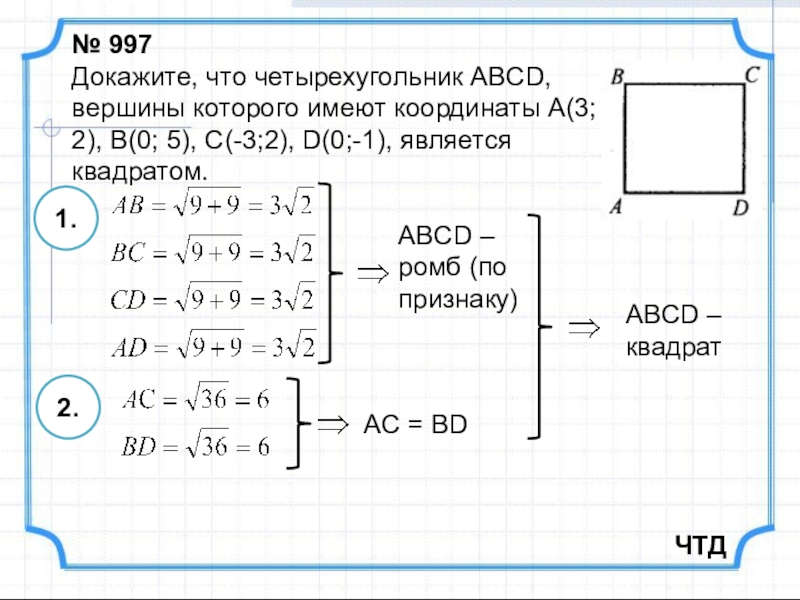
Слайд 20№ 997
Докажите, что четырехугольник ABCD, вершины которого имеют координаты A(3; 2),
1.
ABCD – ромб (по признаку)
2.
AC = BD
ABCD – квадрат
ЧТД
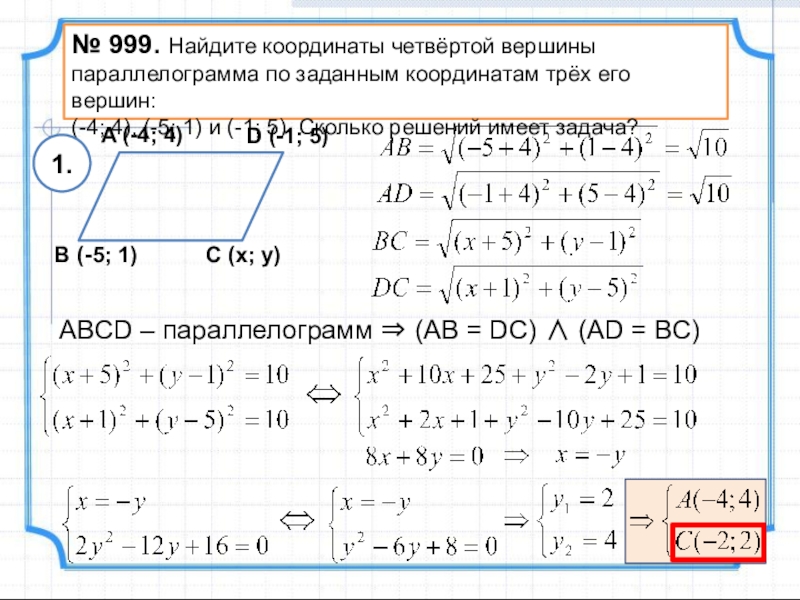
Слайд 21№ 999. Найдите координаты четвёртой вершины параллелограмма по заданным координатам трёх
(-4; 4), (-5; 1) и (-1; 5). Сколько решений имеет задача?
ABCD – параллелограмм (AB = DC) (AD = BC)
1.
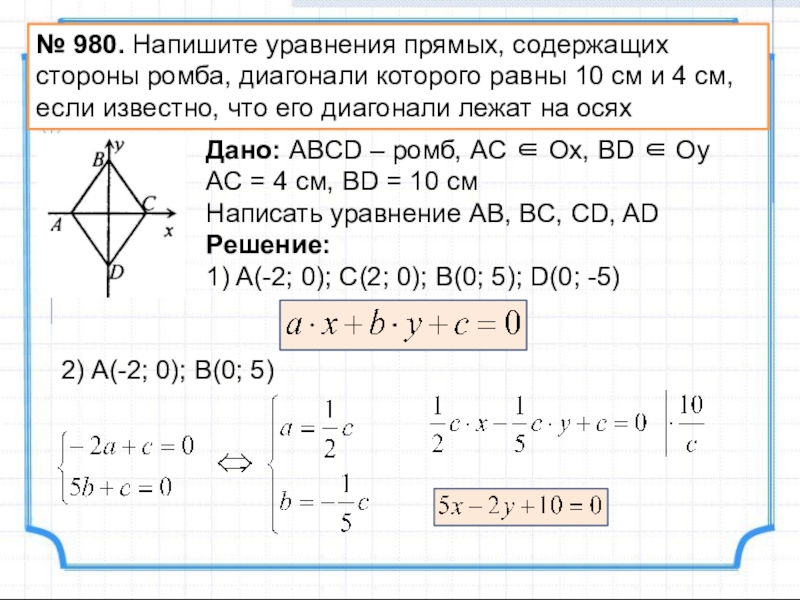
Слайд 23№ 980. Напишите уравнения прямых, содержащих стороны ромба, диагонали которого равны
Дано: ABCD – ромб, AC Ox, BD Oy
AC = 4 см, BD = 10 см
Написать уравнение AB, BC, CD, AD
Решение:
1) A(-2; 0); C(2; 0); B(0; 5); D(0; -5)
2) A(-2; 0); B(0; 5)
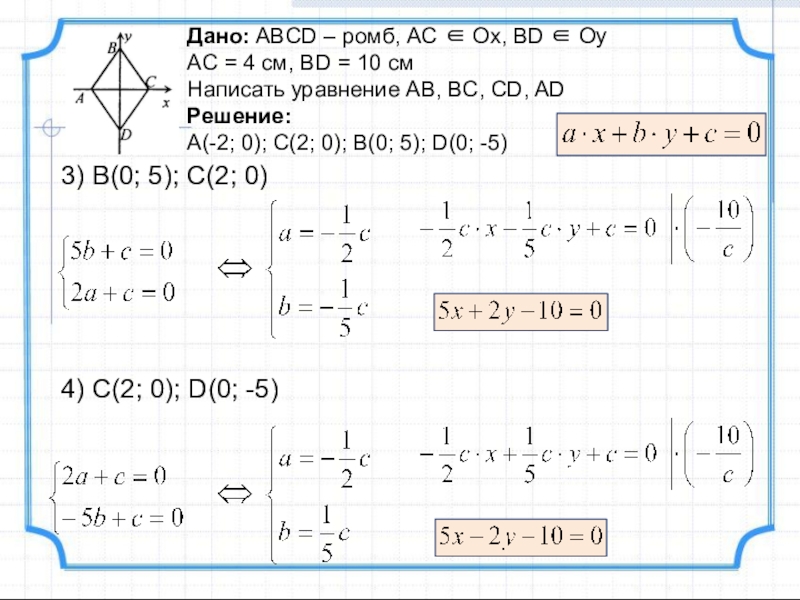
Слайд 24Дано: ABCD – ромб, AC Ox, BD Oy
AC =
Написать уравнение AB, BC, CD, AD
Решение:
A(-2; 0); C(2; 0); B(0; 5); D(0; -5)
3) B(0; 5); C(2; 0)
4) C(2; 0); D(0; -5)
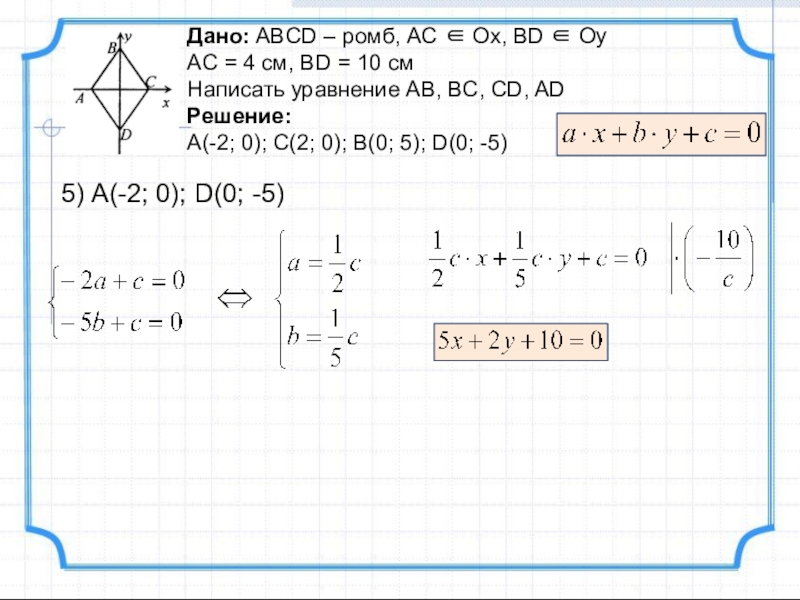
Слайд 25Дано: ABCD – ромб, AC Ox, BD Oy
AC =
Написать уравнение AB, BC, CD, AD
Решение:
A(-2; 0); C(2; 0); B(0; 5); D(0; -5)
5) A(-2; 0); D(0; -5)
Слайд 26№ 1007. Докажите, что отрезок, соединяющий середины диагоналей трапеции, равен полуразности
Дано: ABCD – трапеция,
MAC, AM=MC, NBD, BN=ND.
Доказать:
MN = ½ (AD – BC)
Доказательство:
ЧТД
Слайд 27Домашнее задание
П. 93-94, №966, №969(б), №981, 1002(б)
П. 95-96, №972(б), №979, №984
№990,
Подготовиться к КР