- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Трапеция и ее свойства.
Содержание
- 1. Трапеция и ее свойства.
- 2. Слайд 2
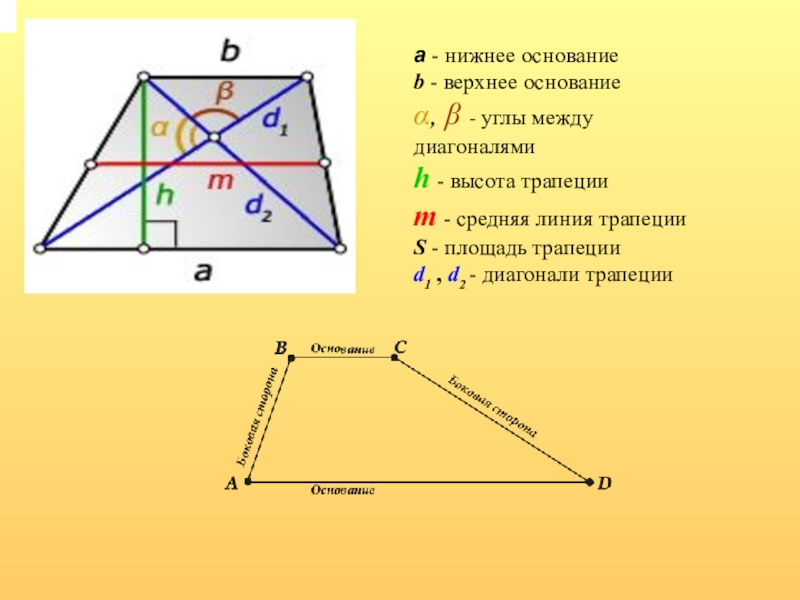
- 3. a - нижнее основаниеb - верхнее основаниеα, β - углы между диагоналямиh - высота трапецииm - средняя линия трапецииS - площадь трапецииd1 , d2 - диагонали трапеции
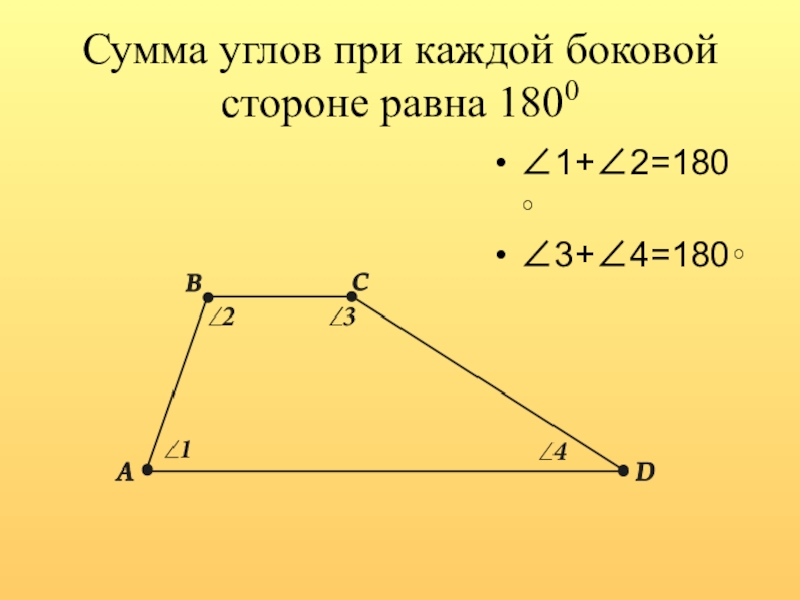
- 4. Сумма углов при каждой боковой стороне равна 1800∠1+∠2=180∘∠3+∠4=180∘
- 5. Биссектриса любого угла отсекает на ее основании
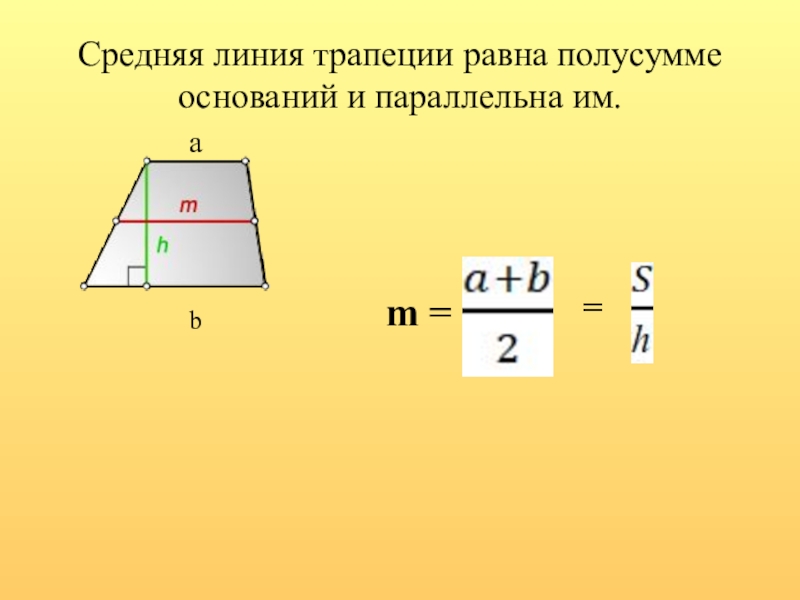
- 6. Средняя линия трапеции равна полусумме оснований и параллельна им.ab m = =
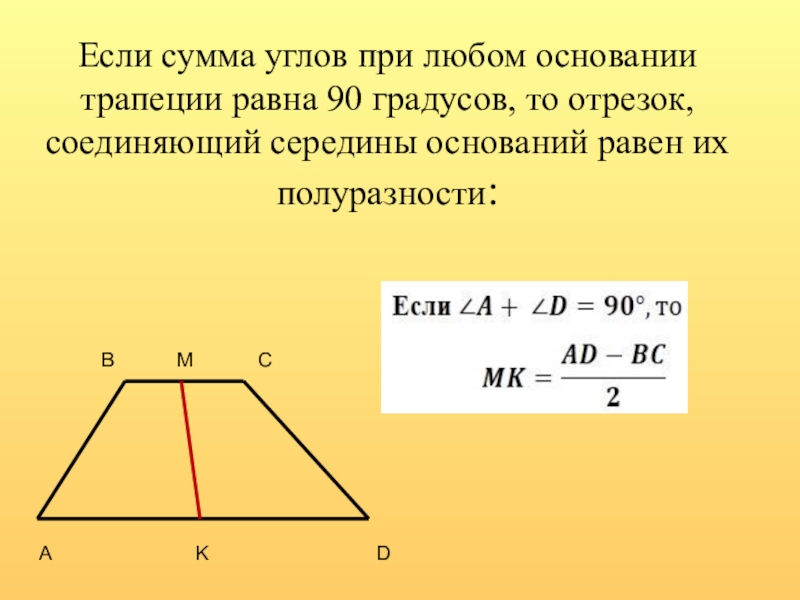
- 7. Если сумма углов при любом основании
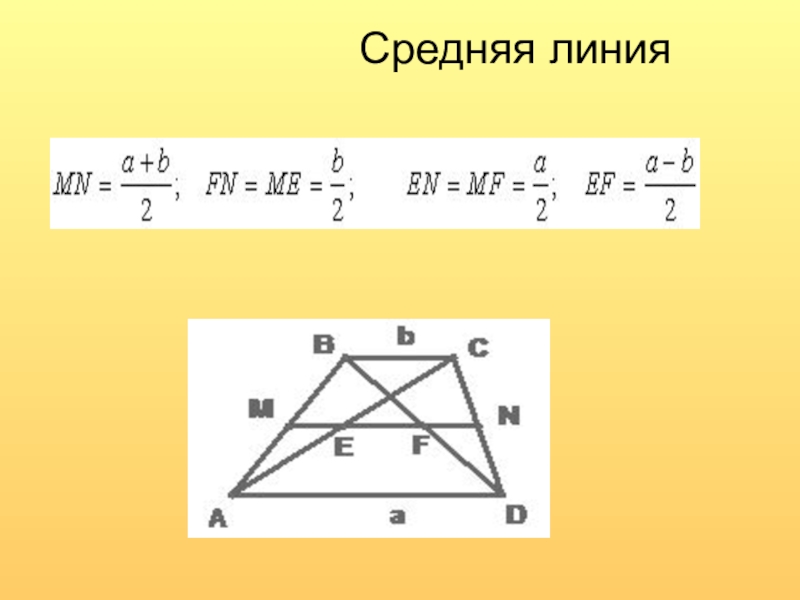
- 8. Средняя линия
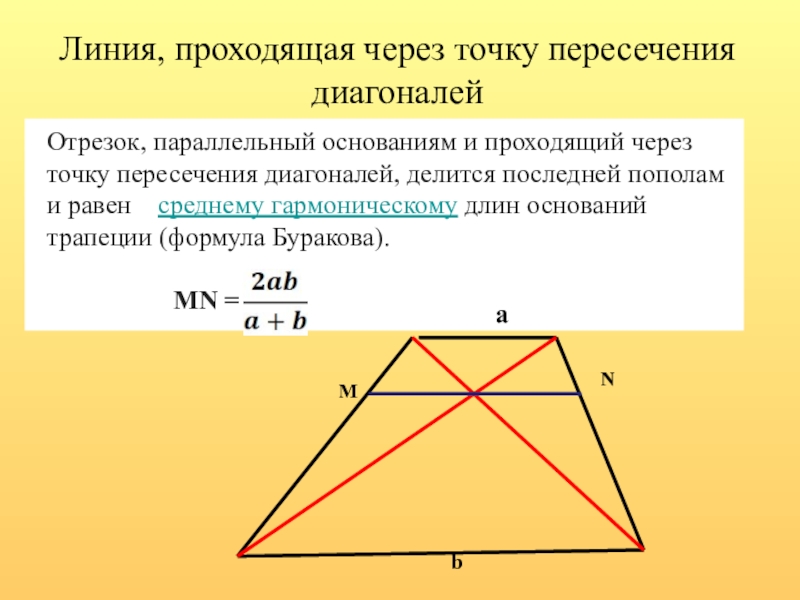
- 9. Линия, проходящая через точку пересечения диагоналейОтрезок, параллельный
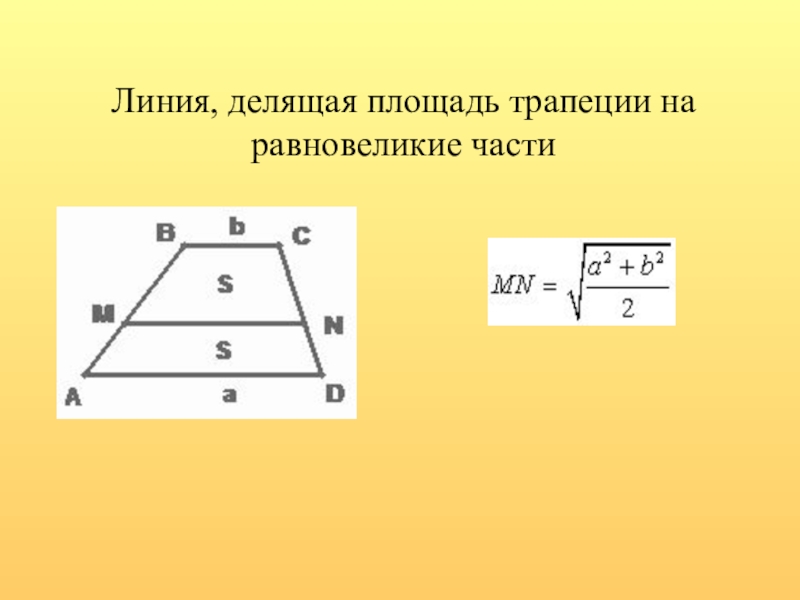
- 10. Линия, делящая площадь трапеции на равновеликие части
- 11. В трапеции с перпендикулярными диагоналями:
- 12. В равнобедренной трапеции равны не только
- 13. В любой трапеции следующие четыре точки лежат на одной
- 14. Если продлить стороны трапеции в сторону меньшего
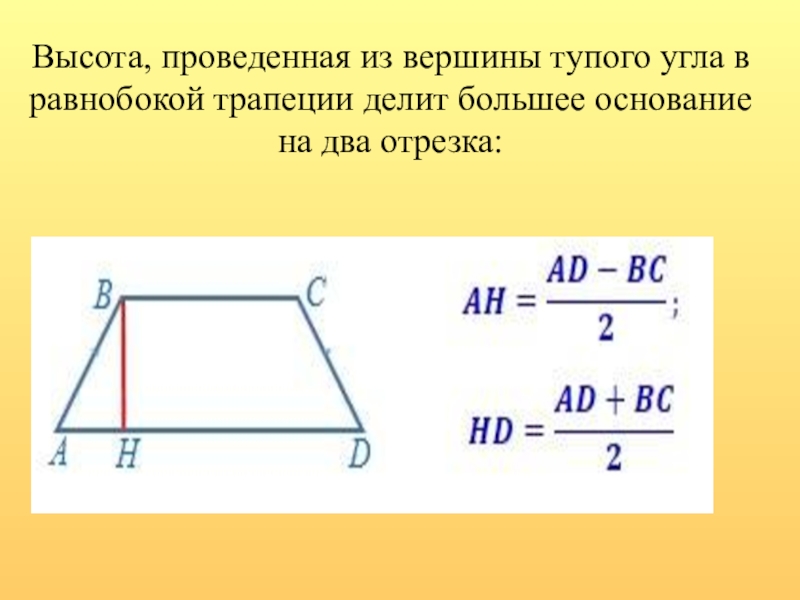
- 15. Высота, проведенная из вершины тупого угла в равнобокой трапеции делит большее основание на два отрезка:
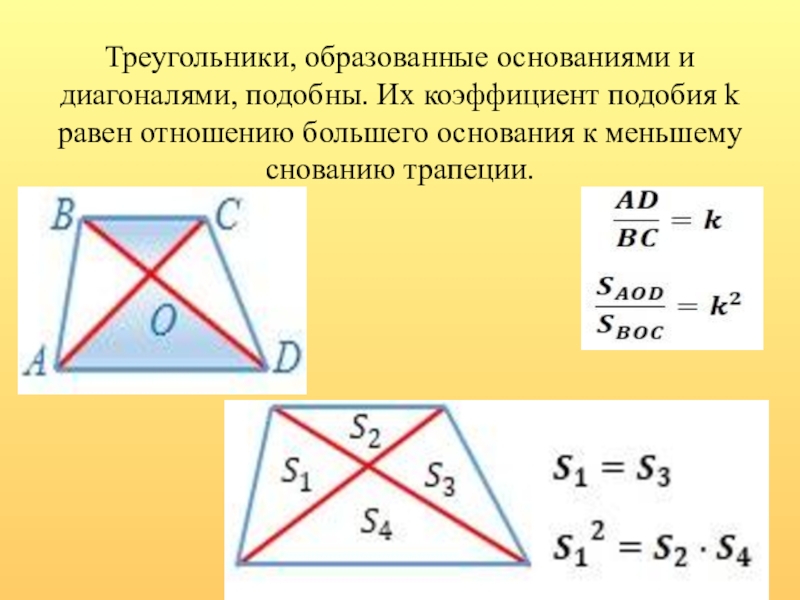
- 16. Треугольники, образованные основаниями и диагоналями, подобны. Их
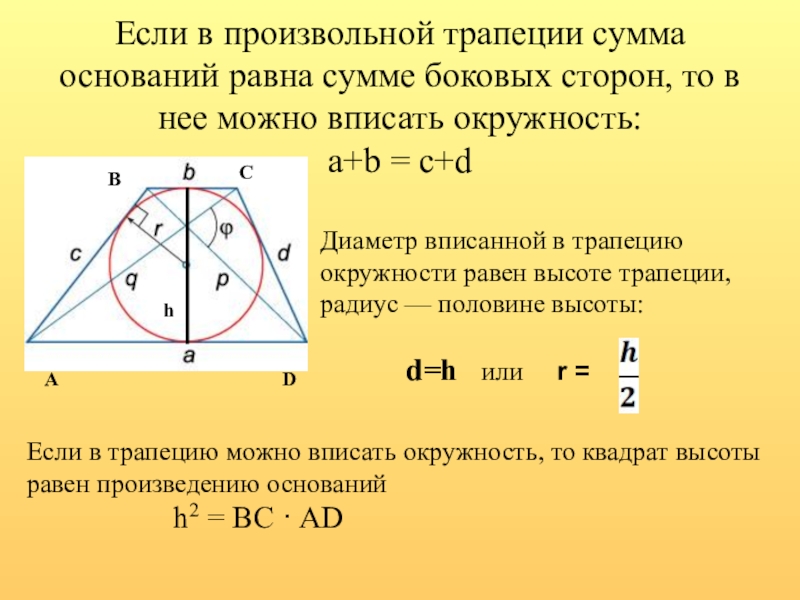
- 17. Если в произвольной трапеции сумма оснований
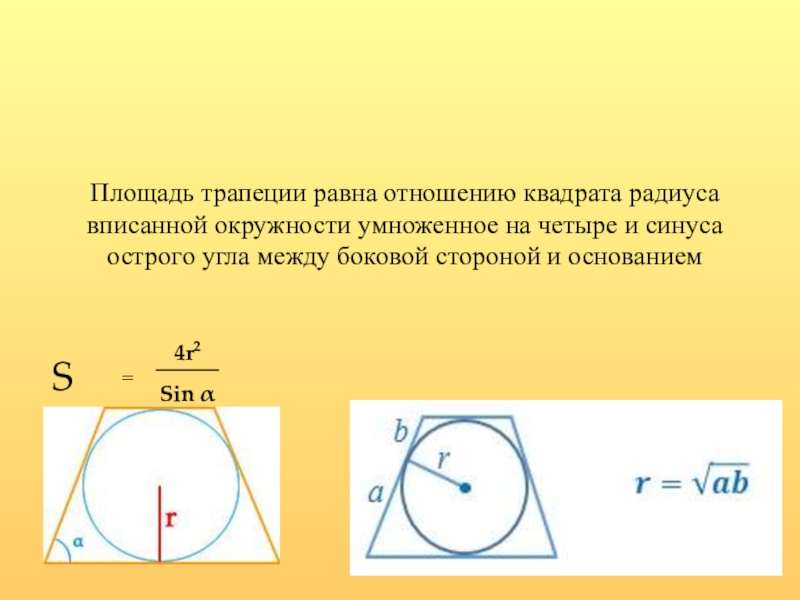
- 18.
- 19. В трапецию можно вписать окружность, если: сумма
- 20. Формулы в помощь: *Cредняя
- 21. Описанная окру́жность многоугольника — окружность, содержащая все вершины
- 22. Окружность, описанная около трапеции.
Слайд 1
Трапеция и ее свойства.
Работу выполнила учитель математики
Снегурова А.М.
МБОУ СОШ №5
Тот, кто учится самостоятельно, достигнет в семь раз больше того, кому все разъясняется.
Артур Гитерман.
Слайд 2
Элементы трапеции
Трапеция — четырехугольник,
Элементы трапеции:
Основания трапеции - параллельные стороны
Боковые стороны - две другие стороны
Средняя линия - отрезок, соединяющий середины боковых сторон.
Вторая средняя линия - отрезок, соединяющий середины оснований.
Диагонали трапеции – это отрезки, соединяющие противоположные вершины трапеции.
Высота трапеции - это расстояние между основаниями .
Слайд 3a - нижнее основание
b - верхнее основание
α, β - углы между диагоналями
h - высота трапеции
m - средняя линия
S - площадь трапеции
d1 , d2 - диагонали трапеции
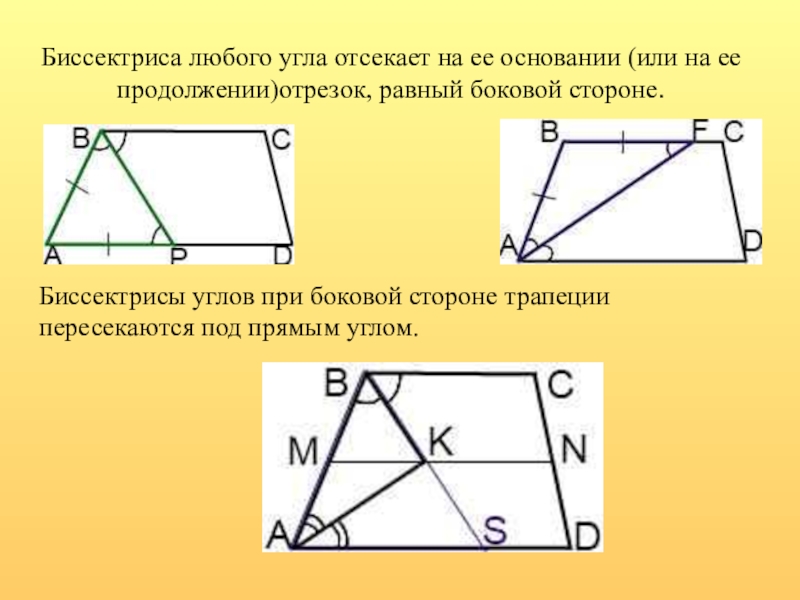
Слайд 5Биссектриса любого угла отсекает на ее основании (или на ее продолжении)отрезок,
Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
Слайд 7 Если сумма углов при любом основании трапеции равна 90 градусов, то
В
А
С
М
D
K
Слайд 9Линия, проходящая через точку пересечения диагоналей
Отрезок, параллельный основаниям и проходящий через
MN =
M
N
a
b
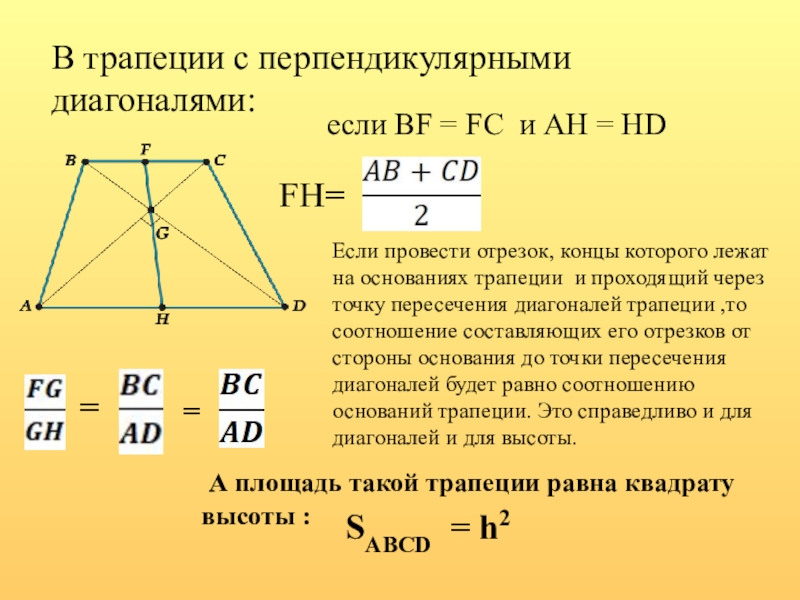
Слайд 11В трапеции с перпендикулярными диагоналями:
FH=
SABCD = h2
если BF =
Если провести отрезок, концы которого лежат на основаниях трапеции и проходящий через точку пересечения диагоналей трапеции ,то соотношение составляющих его отрезков от стороны основания до точки пересечения диагоналей будет равно соотношению оснований трапеции. Это справедливо и для диагоналей и для высоты.
А площадь такой трапеции равна квадрату высоты :
=
=
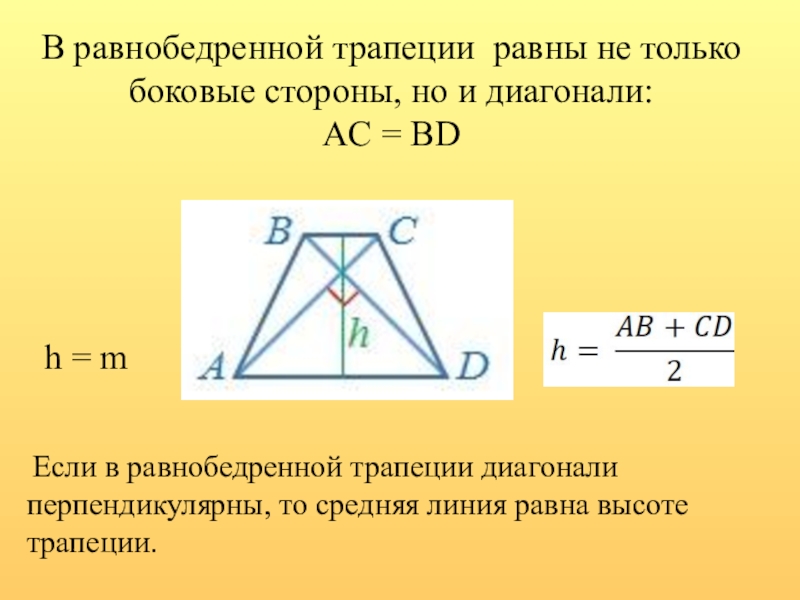
Слайд 12 В равнобедренной трапеции равны не только боковые стороны, но и диагонали: AC
h = m
Если в равнобедренной трапеции диагонали перпендикулярны, то средняя линия равна высоте трапеции.
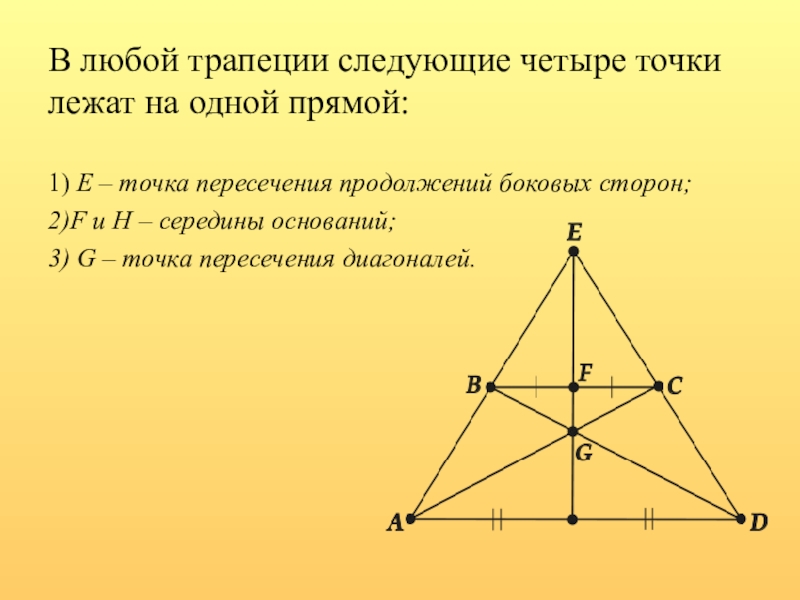
Слайд 13В любой трапеции следующие четыре точки лежат на одной прямой:
1) E – точка пересечения продолжений боковых
2)F и H – середины оснований;
3) G – точка пересечения диагоналей.
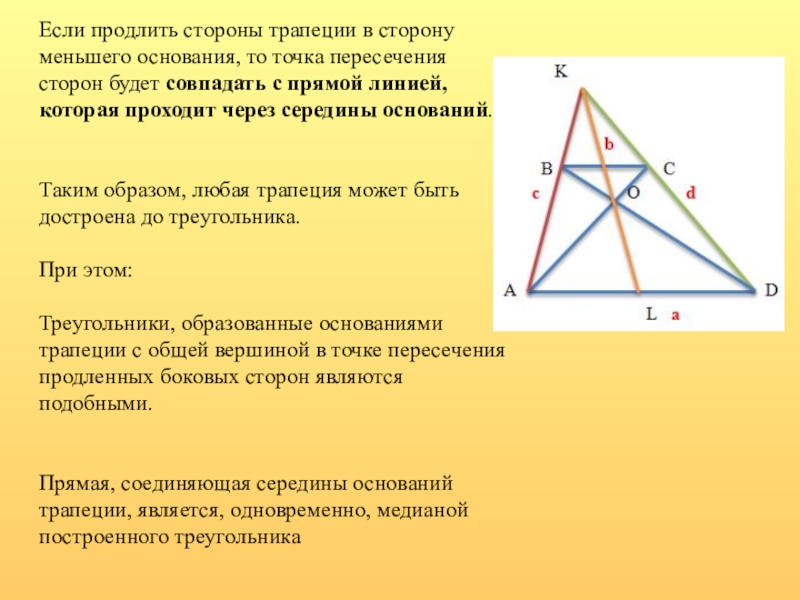
Слайд 14Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения
Таким образом, любая трапеция может быть достроена до треугольника.
При этом:
Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными.
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Слайд 15Высота, проведенная из вершины тупого угла в равнобокой трапеции делит большее
Слайд 16Треугольники, образованные основаниями и диагоналями, подобны. Их коэффициент подобия k равен
Слайд 17 Если в произвольной трапеции сумма оснований равна сумме боковых сторон, то
Диаметр вписанной в трапецию окружности равен высоте трапеции, радиус — половине высоты:
d=h или r =
Если в трапецию можно вписать окружность, то квадрат высоты равен произведению оснований
h2 = BC · AD
h
A
B
C
D
Слайд 18 Площадь трапеции равна отношению квадрата радиуса вписанной окружности умноженное на
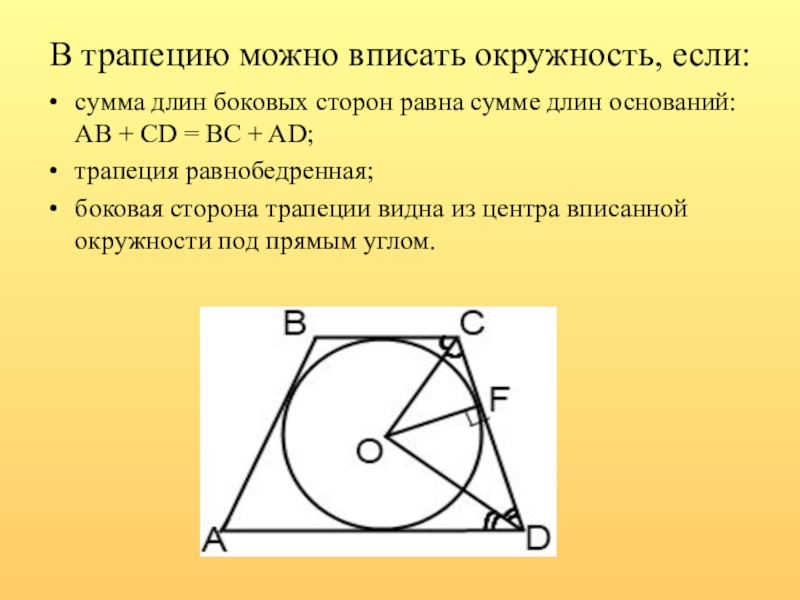
Слайд 19В трапецию можно вписать окружность, если:
сумма длин боковых сторон равна сумме
трапеция равнобедренная;
боковая сторона трапеции видна из центра вписанной окружности под прямым углом.
Слайд 20
Формулы в помощь:
*Cредняя линия через площадь и высоту:
*Высота
*Высота через площадь и длину средней линии:
*Площадь через среднюю линию и высоту S= h·m
*В равнобедренной трапеции длина диагонали равна d =
где с – боковая сторона, a и b – основания или
d =
*Длина основания через среднюю линию и другое основание
a = 2m - b и b = 2m - a
Слайд 21 Описанная окру́жность многоугольника — окружность, содержащая все вершины
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
Слайд 22 Окружность, описанная около трапеции. Четырехугольник можно вписать в окружность тогда и
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции.