- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Тесты по геометрии 7 класс
Содержание
- 1. Тесты по геометрии 7 класс
- 2. Сколько различных прямых можно провести через две точки?1) Три.2) Две.3) Одну.
- 3. 2. Точка М – середина отрезка АВ.Тогда
- 4. Какое предложение неверное? 1) В – середина АС.2) С – середина BD.3) B – середина АD.3.AB=BC=CD=DEABCDE
- 5. 4. Точки А, В и С лежат
- 6. 5. Луч ОК – биссектриса угла АОМ.Тогда неверно, что…∠ АOК =0,5∠ AOM∠ АOК= ∠ KOM∠AOM=0,5∠KOM
- 7. 6. Смежные углы могут быть равны…1) 36° и 154°;2) 59° и 121°;3) 93° и 77°.
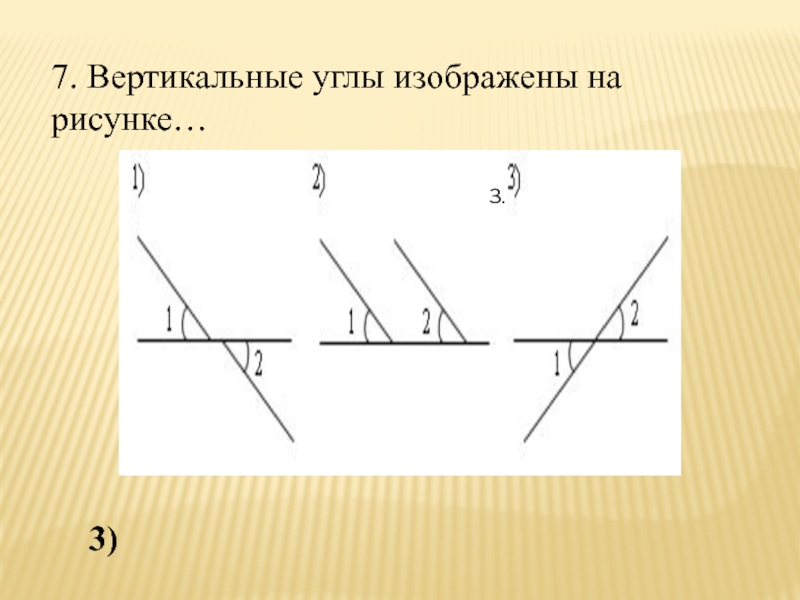
- 8. 7. Вертикальные углы изображены на рисунке…3.3)
- 9. 8. Один из смежных углов тупой.Тогда второй угол – …1) острый;2) прямой;3) тупой.
- 10. 9. Какое предложение неверное?1) Если смежные углы
- 11. Медианы, биссектрисы и высоты треугольника
- 12. Медианой треугольника называется отрезок, соединяющий…1) две стороны
- 13. 2. Треугольник является равнобедренным, если…1) биссектриса треугольника
- 14. 3. Какое высказывание неверное?1) Если медиана и
- 15. 4. Биссектрисы NK и МС треугольника MNF
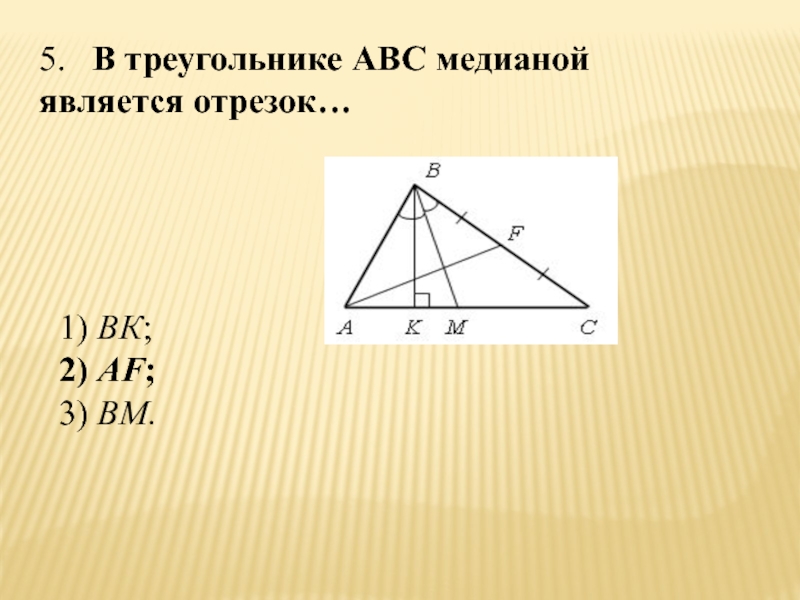
- 16. 5. В треугольнике АВС медианой является
- 17. 6. Какое высказывание неверное?1) Если треугольник равнобедренный,
- 18. 7. Если треугольник равнобедренный, то…1) любая его
- 19. 8. Какое утверждение неверное?1) В равностороннем треугольнике периметр
- 20. 9. Периметр равнобедренного треугольника равен 19 см, основание равно 7 см.Боковая сторона равна…765
- 21. Признаки равенства треугольников
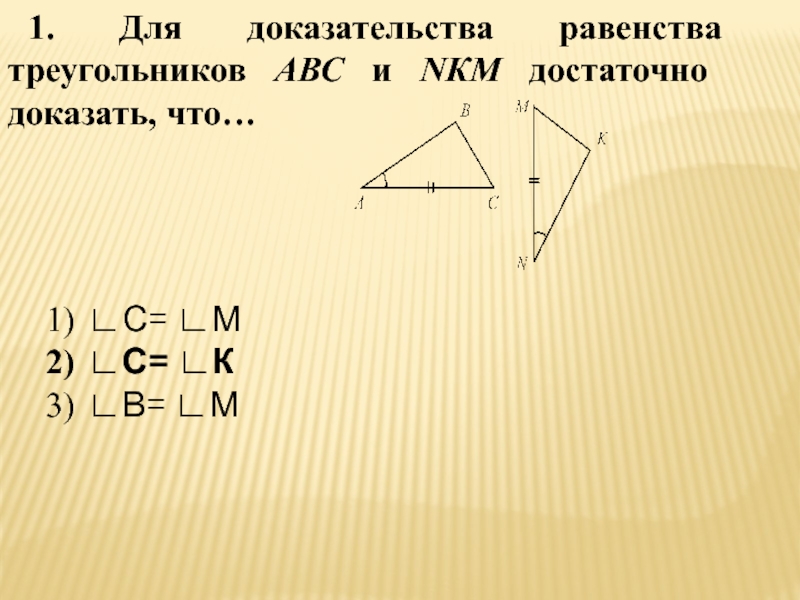
- 22. 1. Для доказательства равенства треугольников АВС и NКМ достаточно доказать, что…∟С= ∟М∟С= ∟К∟В= ∟М
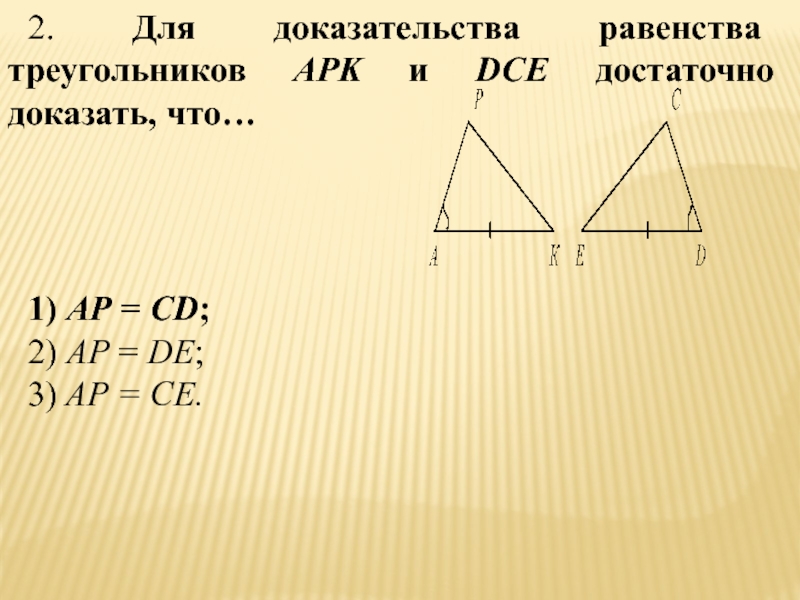
- 23. 2. Для доказательства равенства треугольников АPK и
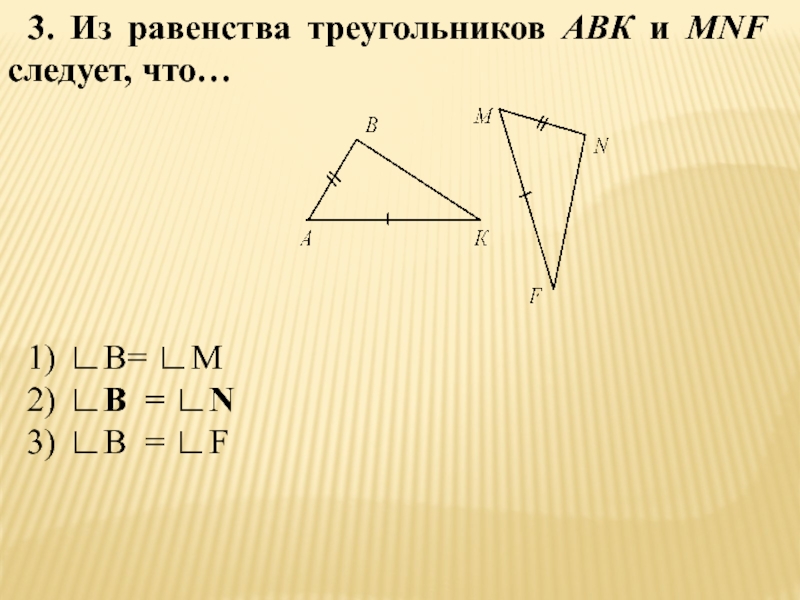
- 24. 3. Из равенства треугольников АВК и MNF следует, что…∟В= ∟M∟B = ∟N∟B = ∟F
- 25. 4. Чтобы доказать равенство двух равнобедренных треугольников,
- 26. 5. Верно, что…1) если сумма двух сторон
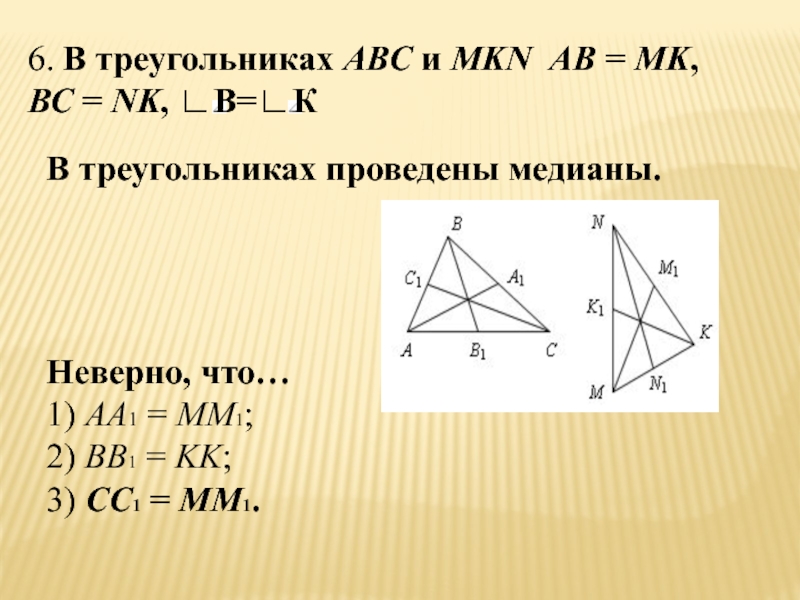
- 27. 6. В треугольниках АВС и MKN АВ
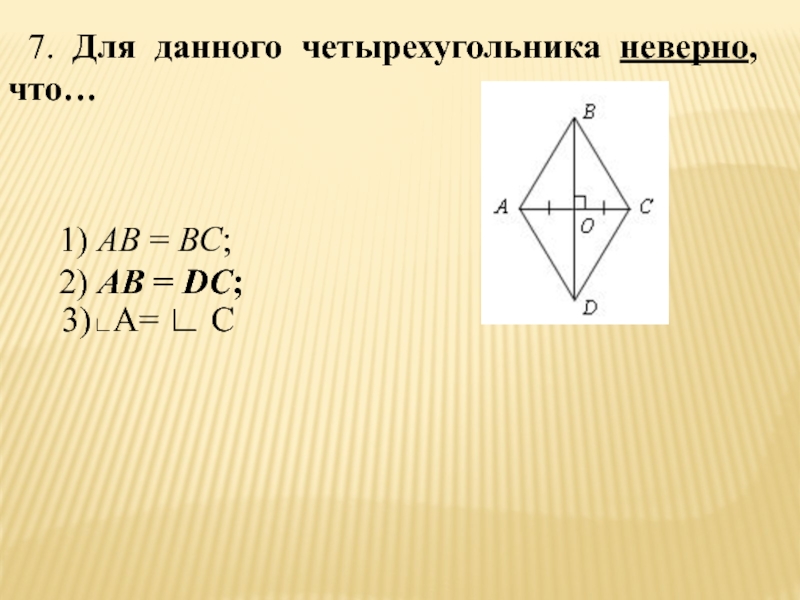
- 28. 7. Для данного четырехугольника неверно, что…1) АВ
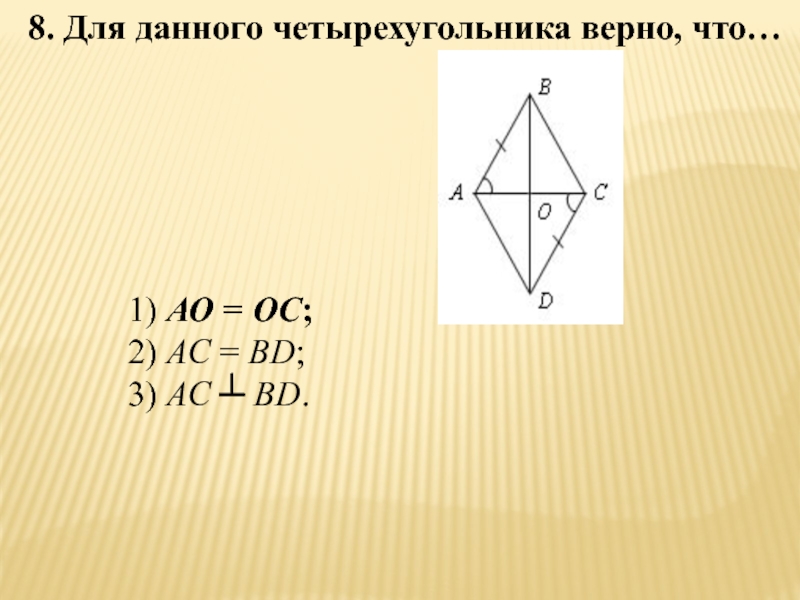
- 29. 8. Для данного четырехугольника верно, что…1) АО = ОС;2) АС = ВD;3) АС ┴ BD.
- 30. 9. Чтобы доказать равенство двух равнобедренных треугольников,
- 31. 10. Какое высказывание неверное?1) Если периметры равносторонних
- 32. ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
- 33. Две прямые на плоскости называются параллельными, если
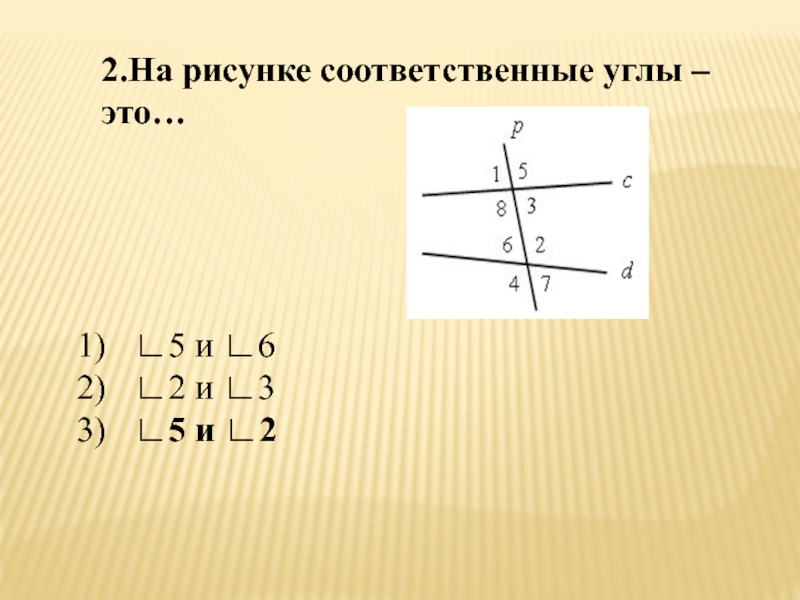
- 34. 2.На рисунке соответственные углы – это…∟5 и ∟6∟2 и ∟3∟5 и ∟2
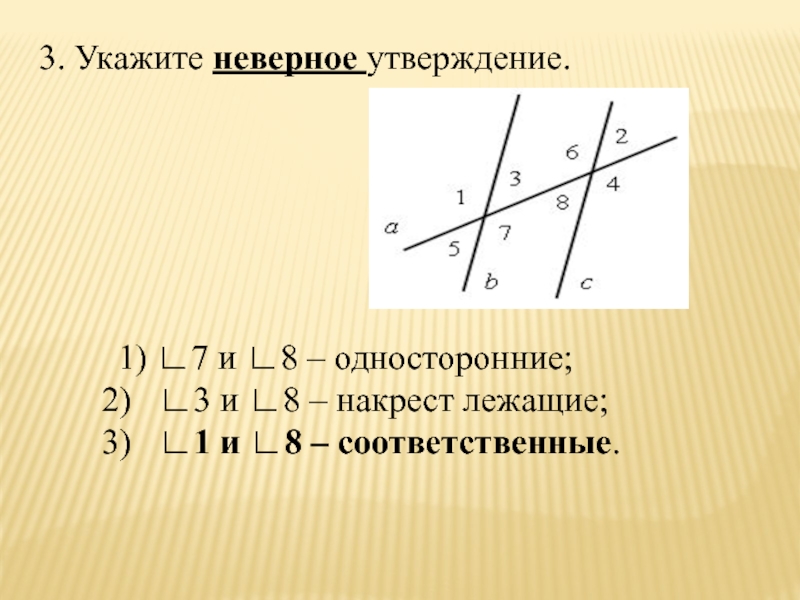
- 35. 3. Укажите неверное утверждение. 1) ∟7 и
- 36. 4. Прямые параллельны, если равны…1) вертикальные углы;2) односторонние углы;3) соответственные углы.
- 37. 5. На рисунке накрест лежащие углы –
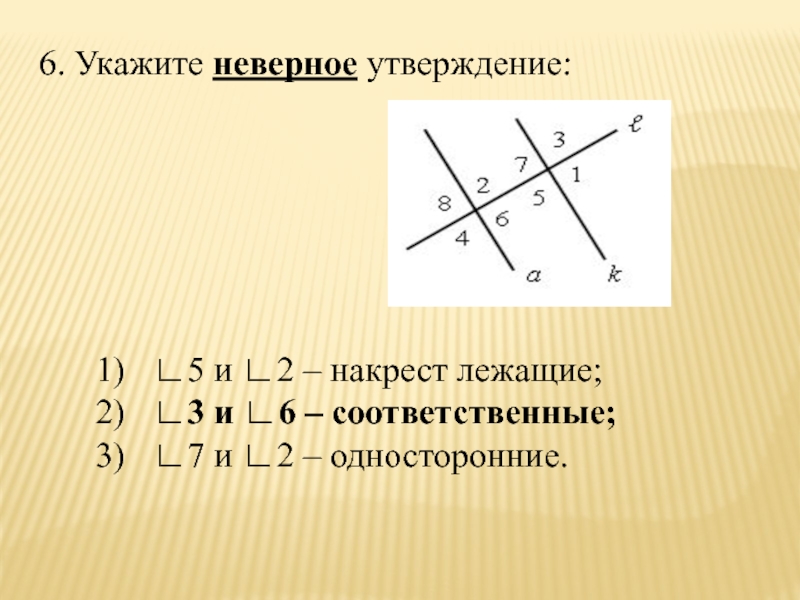
- 38. 6. Укажите неверное утверждение:∟5 и ∟2 –
- 39. 7. Прямые параллельны, если равны…1) смежные углы;2) накрест лежащие углы;3) односторонние углы.
- 40. 8. Если прямая пересекает одну из двух
- 41. УГЛЫ ТРЕУГОЛЬНИКА
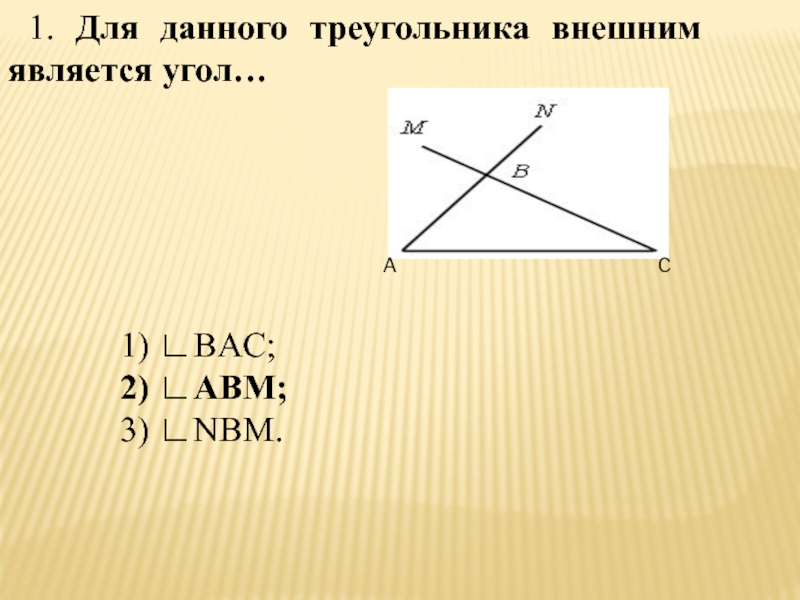
- 42. 1. Для данного треугольника внешним является угол…1) ∟BAC;2) ∟ABM;3) ∟NBM.AC
- 43. 2. Для данного треугольника MNK сумма каких углов равна 80°?1) ∟M+ ∟K;2) ∟N+ ∟K;3) ∟N+ ∟M.
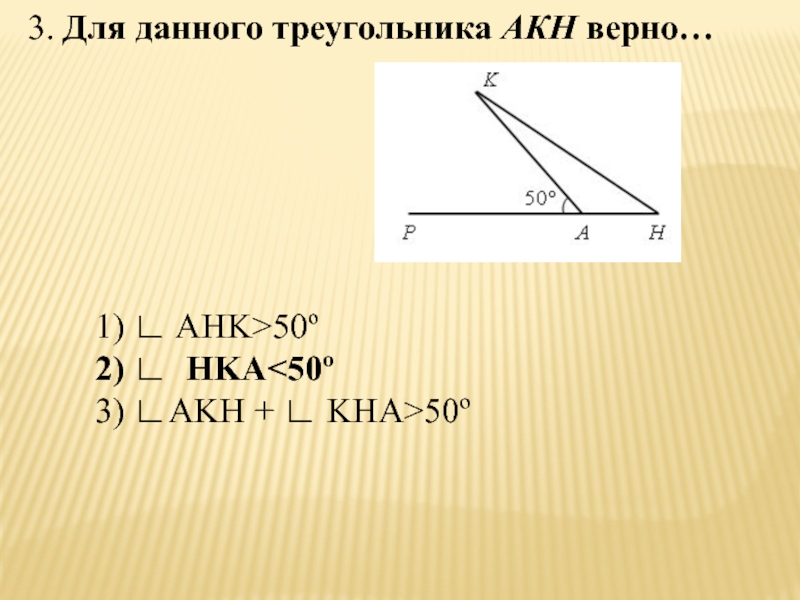
- 44. 3. Для данного треугольника АКН верно…1) ∟ AHK>50º2) ∟ HKA50º
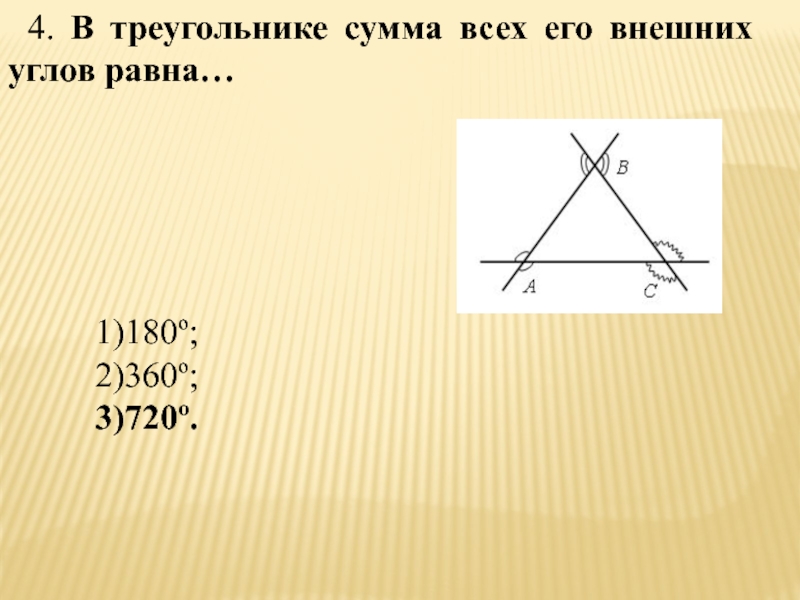
- 45. 4. В треугольнике сумма всех его внешних углов равна…1)180º;2)360º;3)720º.
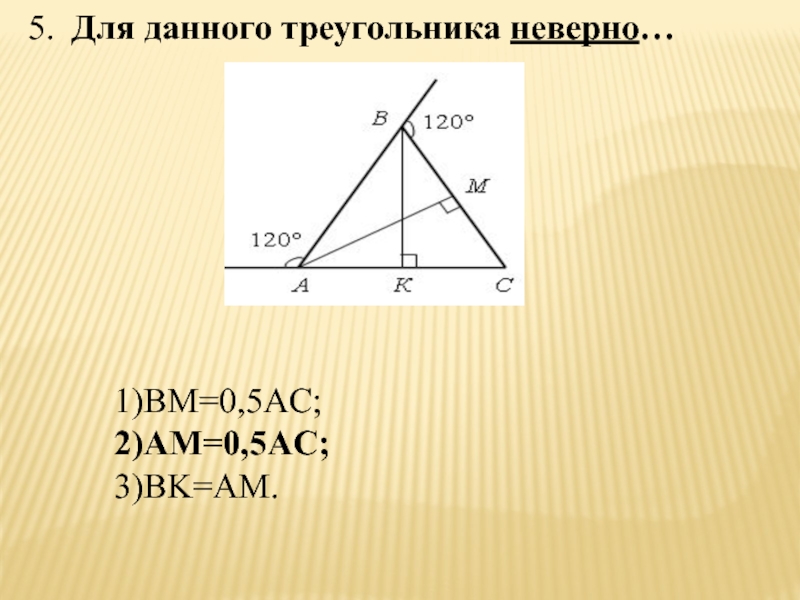
- 46. 5. Для данного треугольника неверно…1)BM=0,5AC;2)AM=0,5AC;3)BK=AM.
- 47. 6. В остроугольном треугольнике любой внешний угол…1) острый;2) прямой;3) тупой.
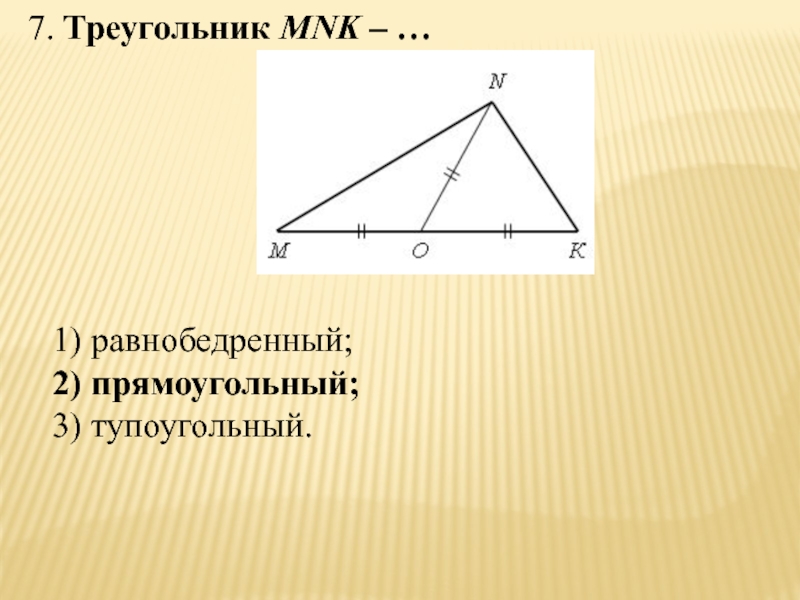
- 48. 7. Треугольник MNK – …1) равнобедренный;2) прямоугольный;3) тупоугольный.
- 49. НЕРАВЕНСТВО ТРЕУГОЛЬНИКА
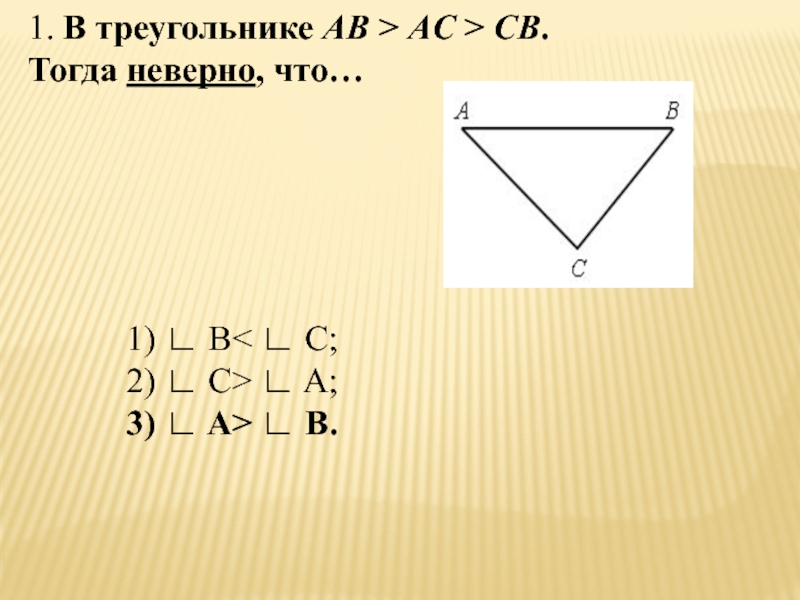
- 50. 1. В треугольнике АВ > AC >
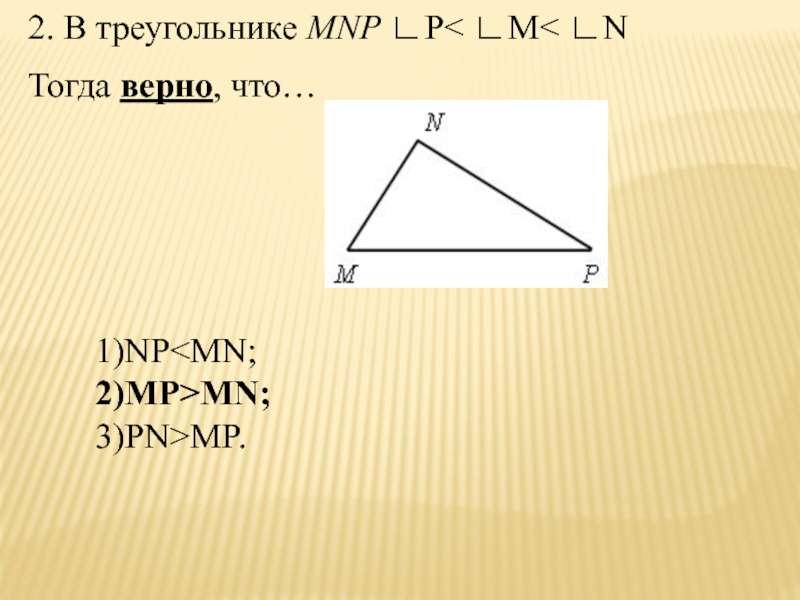
- 51. 2. В треугольнике MNP ∟P< ∟M< ∟N Тогда верно, что…1)NPMN;3)PN>MP.
- 52. 3. Длины сторон одного треугольника могут принимать
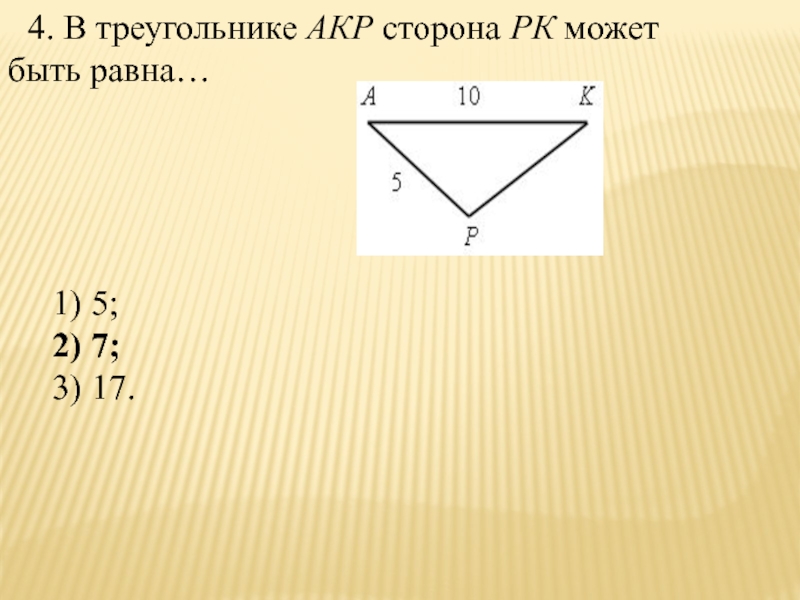
- 53. 4. В треугольнике АКР сторона РК может
- 54. 5. Периметр треугольника равен 24 см. Одна
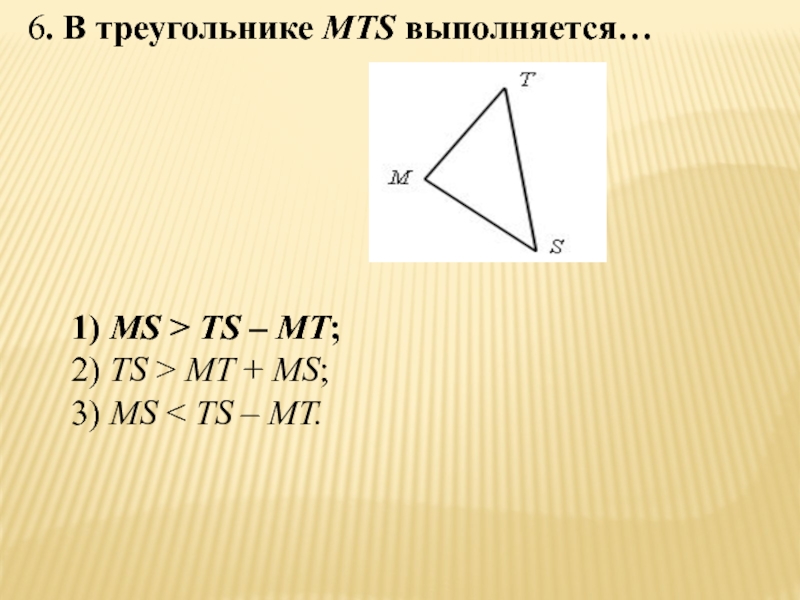
- 55. 6. В треугольнике MTS выполняется…1) MS >
- 56. ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
- 57. В прямоугольном треугольнике острые углы могут быть
- 58. 2. Для сторон данного треугольника справедливо равенство…1) x = z;2) x = y;3) 2y = z.
- 59. 3. Для сторон данного треугольника справедливо равенство…1)
- 60. 4. Из равенства каких элементов не следует,
- 61. 5. Если в треугольнике медиана равна половине
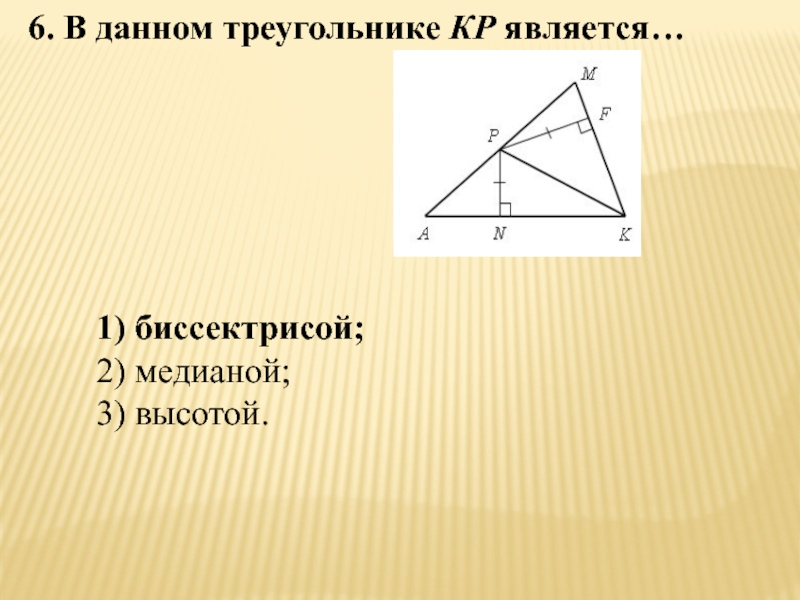
- 62. 6. В данном треугольнике КР является…1) биссектрисой;2) медианой;3) высотой.
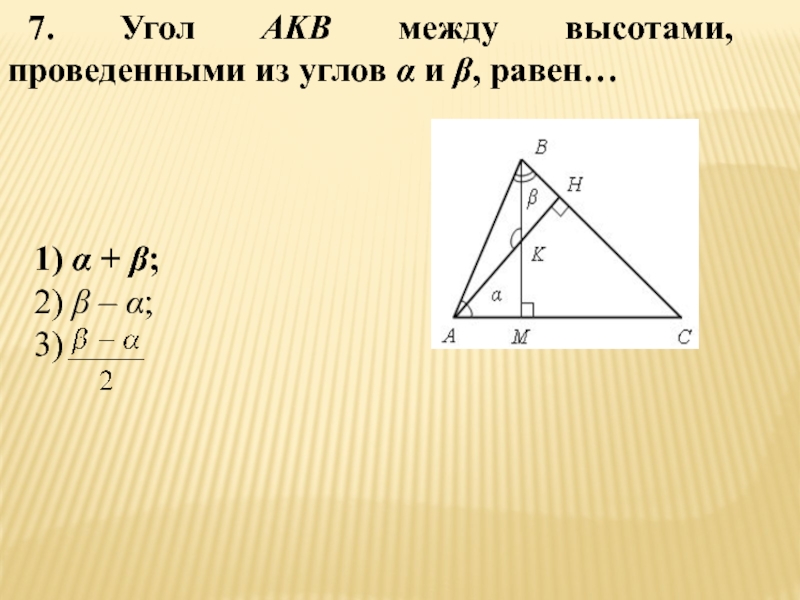
- 63. 7. Угол АKB между высотами, проведенными из
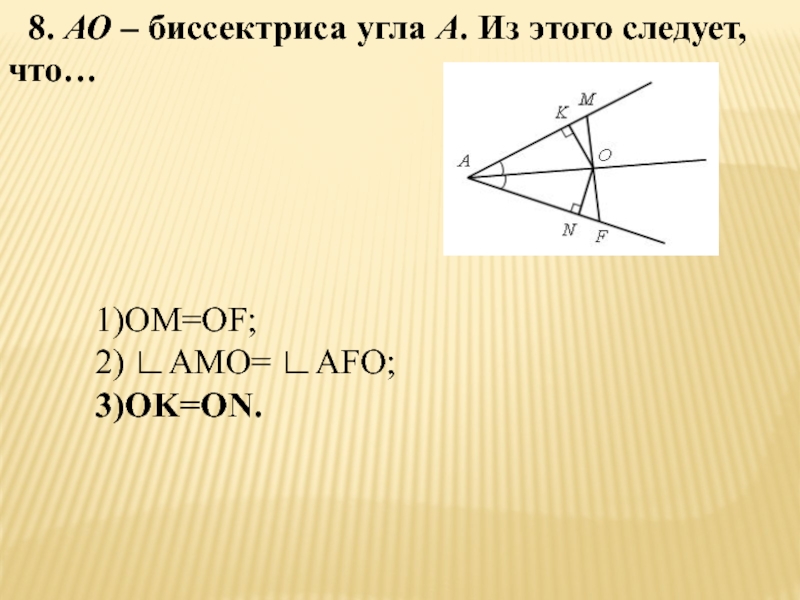
- 64. 8. АО – биссектриса угла А. Из этого следует, что…1)OM=OF;2) ∟AMO= ∟AFO;3)OK=ON.
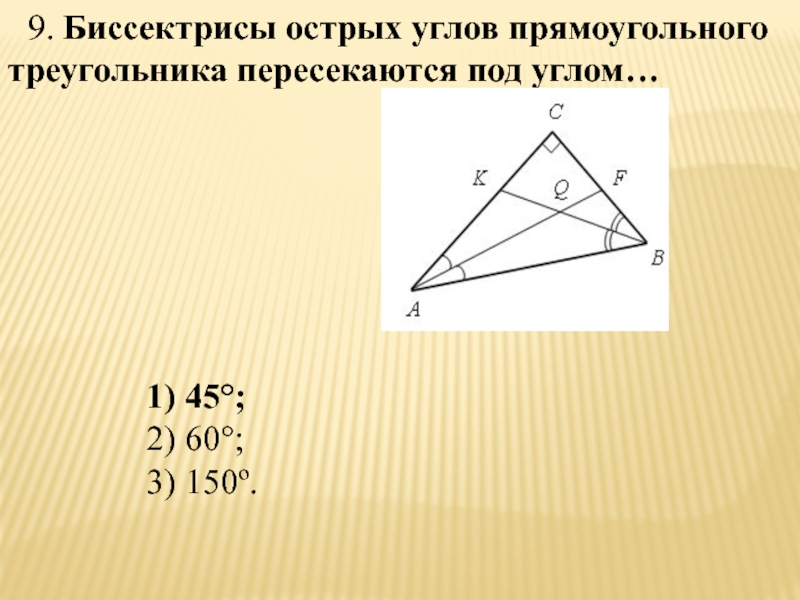
- 65. 9. Биссектрисы острых углов прямоугольного треугольника пересекаются под углом…1) 45°;2) 60°;3) 150º.
- 66. ОКРУЖНОСТЬ
- 67. 1. Диаметр окружности – это…1) два радиуса,
- 68. 2. Центр окружности – это…1) точка, куда
- 69. 3. Дуга окружности – это…1) часть окружности,
- 70. 4. Определить на сколько дуг делят окружность
- 71. 5. Как изображается хорда на чертеже окружности?
- 72. 6. Как называется отрезок, соединяющий центр окружности с любой точкой окружности?1)длина окружности2)радиус окружности3) половина диаметра окружности
Сколько различных прямых можно провести через две точки?1) Три.2) Две.3) Одну.
Слайд 4Какое предложение неверное?
1) В – середина АС.
2) С – середина
BD.
3) B – середина АD.
3) B – середина АD.
3.
AB=BC=CD=DE
A
B
C
D
E
Слайд 54. Точки А, В и С лежат на одной прямой.
АВ =
13,5 см, АС = 9,8 см, СВ = 3,7 см.
Тогда…
Тогда…
С € АВ
А € СВ
В € АВ
Слайд 109. Какое предложение неверное?
1) Если смежные углы равны, то они прямые.
2)
Если углы прямые, то они смежные.
3) Если углы вертикальные, то они равны.
3) Если углы вертикальные, то они равны.
Слайд 12Медианой треугольника называется отрезок, соединяющий…
1) две стороны треугольника;
2) середины двух сторон
треугольника;
3) вершину и середину противоположной стороны.
3) вершину и середину противоположной стороны.
Слайд 132. Треугольник является равнобедренным, если…
1) биссектриса треугольника совпадает с его высотой;
2)
медиана треугольника является его высотой и биссектрисой;
3) любая медиана является высотой.
3) любая медиана является высотой.
Слайд 143. Какое высказывание неверное?
1) Если медиана и высота, проведенные из одной
вершины треугольника, не совпадают, то этот треугольник не является равнобедренным.
2) Если биссектриса треугольника делит противоположную сторону на равные отрезки, то этот треугольник равнобедренный.
3) Если треугольник равносторонний, то сумма длин его высот равна сумме длин его биссектрис.
2) Если биссектриса треугольника делит противоположную сторону на равные отрезки, то этот треугольник равнобедренный.
3) Если треугольник равносторонний, то сумма длин его высот равна сумме длин его биссектрис.
Слайд 154. Биссектрисы NK и МС треугольника MNF пересекаются в точке О.
Тогда
FO – …
1) высота;
2) биссектриса;
3) медиана.
Слайд 176. Какое высказывание неверное?
1) Если треугольник равнобедренный, то любая его биссектриса
является и медианой.
2) Если хотя бы одна высота треугольника делит его противоположную сторону пополам, то этот треугольник равнобедренный.
3) Если треугольник равносторонний, то длина любой его высоты равна длине любой его биссектрисы.
2) Если хотя бы одна высота треугольника делит его противоположную сторону пополам, то этот треугольник равнобедренный.
3) Если треугольник равносторонний, то длина любой его высоты равна длине любой его биссектрисы.
Слайд 187. Если треугольник равнобедренный, то…
1) любая его биссектриса является и высотой;
2)
медианы, проведенные к боковым сторонам, равны;
3) наименьшей из сторон является основание.
3) наименьшей из сторон является основание.
Слайд 198. Какое утверждение неверное?
1) В равностороннем треугольнике периметр в 3 раза больше
одной из его сторон.
2) Если в треугольнике периметр в 3 раза больше одной из его сторон, то этот треугольник равносторонний.
3) В равностороннем треугольнике сумма длин медиан равна сумме длин его высот.
2) Если в треугольнике периметр в 3 раза больше одной из его сторон, то этот треугольник равносторонний.
3) В равностороннем треугольнике сумма длин медиан равна сумме длин его высот.
Слайд 209. Периметр равнобедренного треугольника равен 19 см, основание равно 7 см.
Боковая
сторона равна…
7
6
5
7
6
5
Слайд 221. Для доказательства равенства треугольников АВС и NКМ достаточно доказать, что…
∟С=
∟М
∟С= ∟К
∟В= ∟М
∟С= ∟К
∟В= ∟М
Слайд 232. Для доказательства равенства треугольников АPK и DCE достаточно доказать, что…
1)
АР = CD;
2) AP = DE;
3) AP = CE.
2) AP = DE;
3) AP = CE.
Слайд 254. Чтобы доказать равенство двух равнобедренных треугольников, недостаточно доказать равенство…
1) углов
при основаниях;
2) оснований и углов при основаниях;
3) оснований и углов при вершине.
2) оснований и углов при основаниях;
3) оснований и углов при вершине.
Слайд 265. Верно, что…
1) если сумма двух сторон и периметр одного треугольника
соответственно равны сумме двух сторон и периметру другого треугольника, то такие треугольники равны;
2) если сумма двух сторон и угол между ними одного треугольника соответственно равны сумме двух сторон и углу между ними другого треугольника, то такие треугольники равны;
3) если две стороны и периметр одного треугольника соответственно равны двум сторонам и периметру другого треугольника, то такие треугольники равны.
2) если сумма двух сторон и угол между ними одного треугольника соответственно равны сумме двух сторон и углу между ними другого треугольника, то такие треугольники равны;
3) если две стороны и периметр одного треугольника соответственно равны двум сторонам и периметру другого треугольника, то такие треугольники равны.
Слайд 276. В треугольниках АВС и MKN АВ = MK,
ВС =
NK, ∟В=∟К
В треугольниках проведены медианы.
Неверно, что…
1) АА1 = MM1;
2) BB1 = KK;
3) CC1 = MM1.
Слайд 309. Чтобы доказать равенство двух равнобедренных треугольников, достаточно доказать равенство…
1) оснований;
2)
боковых сторон;
3) оснований и боковых сторон.
3) оснований и боковых сторон.
Слайд 3110. Какое высказывание неверное?
1) Если периметры равносторонних треугольников равны, то равны
и треугольники.
2) Если периметры равнобедренных треугольников равны, то равны и треугольники.
3) Периметры равных равнобедренных треугольников равны.
2) Если периметры равнобедренных треугольников равны, то равны и треугольники.
3) Периметры равных равнобедренных треугольников равны.
Слайд 33Две прямые на плоскости называются параллельными, если они:
1) пересекаются под
прямым углом;
2) не пересекаются.
2) не пересекаются.
Слайд 353. Укажите неверное утверждение.
1) ∟7 и ∟8 – односторонние;
∟3 и
∟8 – накрест лежащие;
∟1 и ∟8 – соответственные.
∟1 и ∟8 – соответственные.
Слайд 364. Прямые параллельны, если равны…
1) вертикальные углы;
2) односторонние углы;
3) соответственные углы.
Слайд 386. Укажите неверное утверждение:
∟5 и ∟2 – накрест лежащие;
∟3 и ∟6
– соответственные;
∟7 и ∟2 – односторонние.
∟7 и ∟2 – односторонние.
Слайд 397. Прямые параллельны, если равны…
1) смежные углы;
2) накрест лежащие углы;
3) односторонние
углы.
Слайд 408. Если прямая пересекает одну из двух параллельных прямых, то:
1) она
не пересекает другую;
2) она пересекает и другую
2) она пересекает и другую
Слайд 523. Длины сторон одного треугольника могут принимать значения…
1) 16, 19, 28;
2)
39, 63, 24;
3) 80, 25, 54.
3) 80, 25, 54.
Слайд 57В прямоугольном треугольнике острые углы могут быть равны…
1) 42° и 38°;
2)
1°45′ и 88°15′;
3) 56° и 44°.
3) 56° и 44°.
Слайд 593. Для сторон данного треугольника справедливо равенство…
1) с = 0,5 b;
2)
с = 0,5 a;
3) а = 0,5 b.
3) а = 0,5 b.
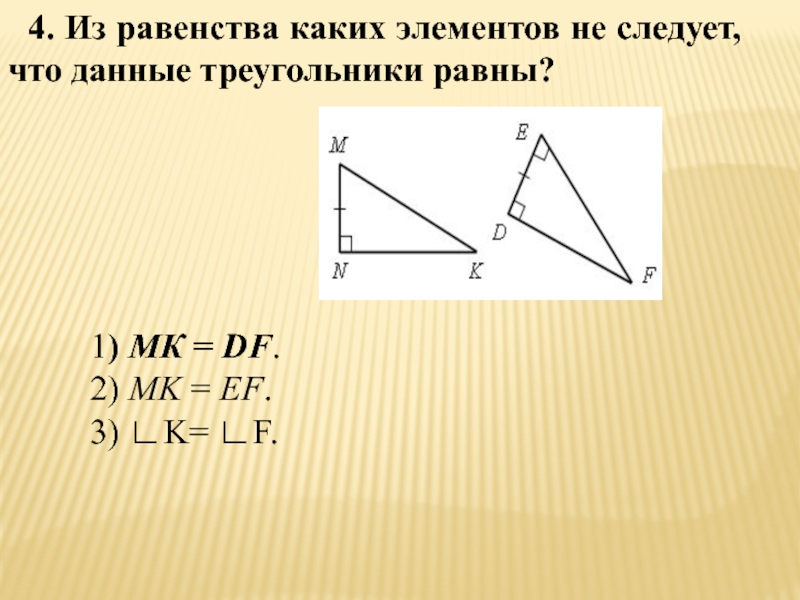
Слайд 604. Из равенства каких элементов не следует, что данные треугольники равны?
1)
МК = DF.
2) MK = EF.
3) ∟K= ∟F.
2) MK = EF.
3) ∟K= ∟F.
Слайд 615. Если в треугольнике медиана равна половине стороны, к которой она
проведена, то этот треугольник…
1) равнобедренный;
2) равносторонний;
3) прямоугольный.
1) равнобедренный;
2) равносторонний;
3) прямоугольный.
Слайд 659. Биссектрисы острых углов прямоугольного треугольника пересекаются под углом…
1) 45°;
2) 60°;
3)
150º.
Слайд 671. Диаметр окружности – это…
1) два радиуса, лежащие на одной прямой
2)
хорда, проходящая через центр окружности
3) прямая, проходящая через две точки и центр окружности
3) прямая, проходящая через две точки и центр окружности
Слайд 682. Центр окружности – это…
1) точка, куда ставится ножка циркуля при
начертания окружности
2) середина окружности
3) точка, равноудалённая от всех точек окружности
2) середина окружности
3) точка, равноудалённая от всех точек окружности
Слайд 693. Дуга окружности – это…
1) часть окружности, выделенная точками
2) часть окружности,
ограниченная двумя точками
3) часть окружности, ограниченная хордами
3) часть окружности, ограниченная хордами
Слайд 704. Определить на сколько дуг делят окружность две точки, лежащие на
окружности. Выбрать правильный ответ:
1) на одну
2) на две
Слайд 715. Как изображается хорда на чертеже окружности?
1) прямой линией
2) дугой
окружности
3) отрезком с концами, лежащими на окружности
3) отрезком с концами, лежащими на окружности
Слайд 726. Как называется отрезок, соединяющий центр окружности с любой точкой окружности?
1)длина
окружности
2)радиус окружности
3) половина диаметра окружности
2)радиус окружности
3) половина диаметра окружности