- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теорема Пифагора (8 класс)
Содержание
- 1. Теорема Пифагора (8 класс)
- 2. О жизни Пифагора известно немного. Он родился
- 3. О теореме Пифагора Пребудет вечной истина, как
- 4. Формулировка теоремы. « Доказать, что квадрат,
- 5. Современная формулировка:« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
- 6. Доказательства теоремы Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).
- 7. Теорема ПифагораДоказательство:В прямоугольном треугольнике квадрат гипотенузы равен
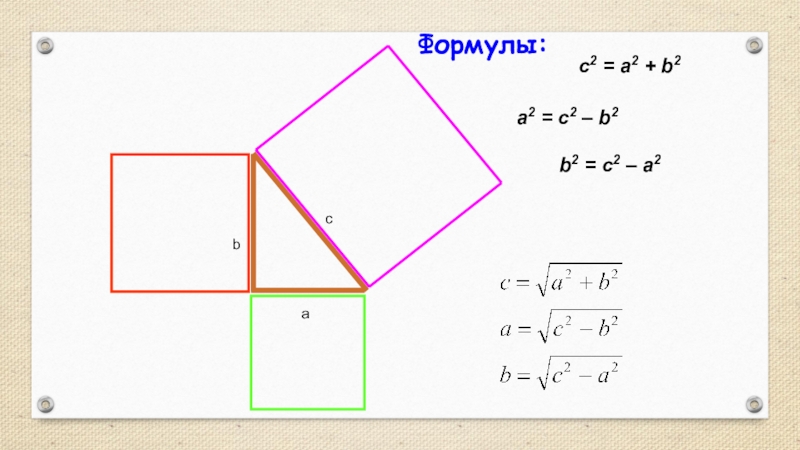
- 8. abc2 = a2 + b2a2 = c2 – b2b2 = c2 – a2Формулы:с
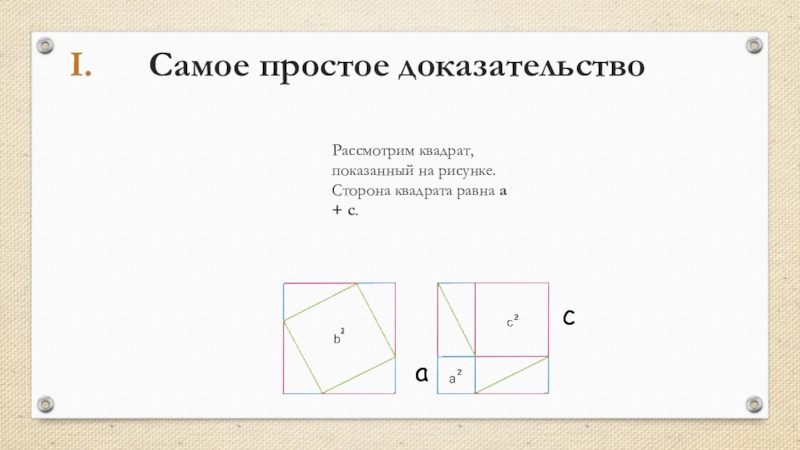
- 9. Самое простое доказательствоРассмотрим квадрат, показанный на рисунке. Сторона квадрата равна a + c. ca
- 10. В одном случае (слева) квадрат
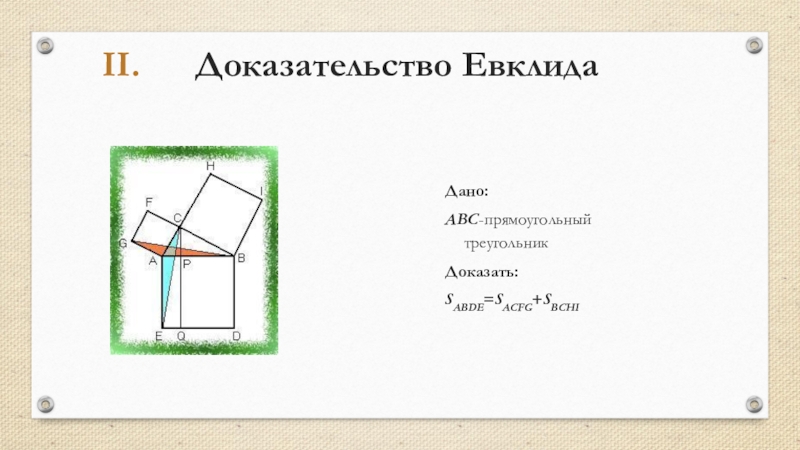
- 11. Доказательство Евклида Дано: ABC-прямоугольный треугольник Доказать:SABDE=SACFG+SBCHI
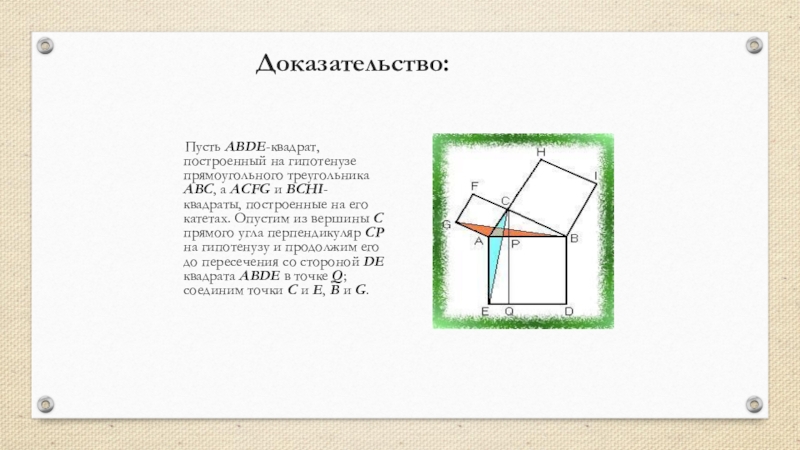
- 12. Доказательство: Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного
- 13. Алгоритм решения задач по теореме Пифагора Внимательно
- 14. Решение задачНайти неизвестную сторону треугольника
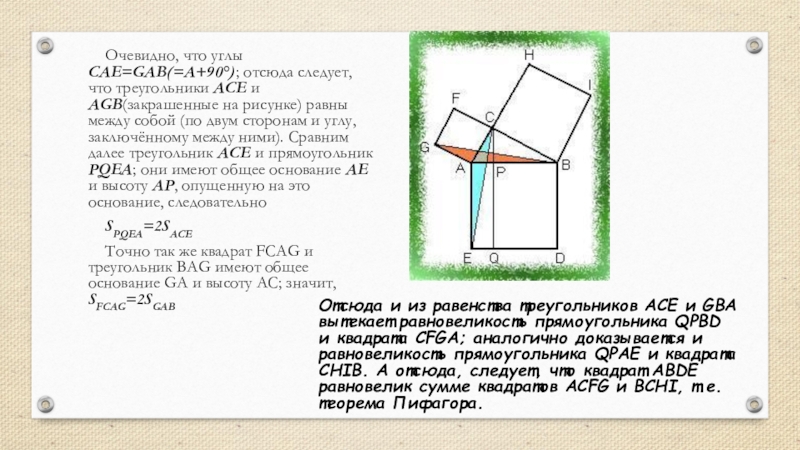
- 15. Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что
- 16. Спасибо за просмотр.
Слайд 1Теорема
Пифагора
Презентацию подготовил: Спесивцев Дмитрий
Школа №4 г. Долгопрудный 8 класс
Учитель математики: Абрамова
Слайд 2О жизни Пифагора известно немного. Он родился в 580 г. до
Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове.
Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет. Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу.
Он поселился в одной из греческих колоний Южной Италии в городе Кротоне. Там Пифагор организовал тайный союз молодёжи из представителей аристократии. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.
(ок. 580 – ок. 500 г. до н.э.)
Слайд 3О теореме Пифагора
Пребудет вечной истина, как скоро
Все познает слабый человек!
И
Слайд 4Формулировка
теоремы.
« Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника,
« Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».
Во времена Пифагора теорема звучала так:
или
Слайд 5Современная формулировка:
« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
Слайд 6Доказательства теоремы
Существует около 500 различных доказательств этой теоремы (геометрических,
Слайд 7Теорема Пифагора
Доказательство:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Дано: прямоугольный
Доказать:c2 = a2 + b2
Слайд 9Самое простое доказательство
Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна a +
c
a
Слайд 10
В одном случае (слева) квадрат разбит на квадрат со
a
c
a
c
В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.
a
c
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.
Слайд 12Доказательство:
Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного треугольника ABC, а ACFG
Слайд 13Алгоритм решения задач по теореме Пифагора
Внимательно прочти задачу, разберись с
По условию сделай чертеж.
Выдели на чертеже прямоугольный треугольник.
Найди катеты и гипотенузу.
Запиши теорему Пифагора и соотнеси данные в задаче с ней.
Выполни подстановку данных.
Соотнеси полученный ответ с вопросом задачи и смыслом условия.
Слайд 15Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники ACE и AGB(закрашенные
SPQEA=2SACE
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, SFCAG=2SGAB
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.