Презентация, доклад на тему Теорема Пифагора

Содержание

Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования» - www.edu-reforma.ru

Слайд 1Теорема Пифагора: с древнейших времен до наших дней
«Геометрия владеет двумя сокровищами:


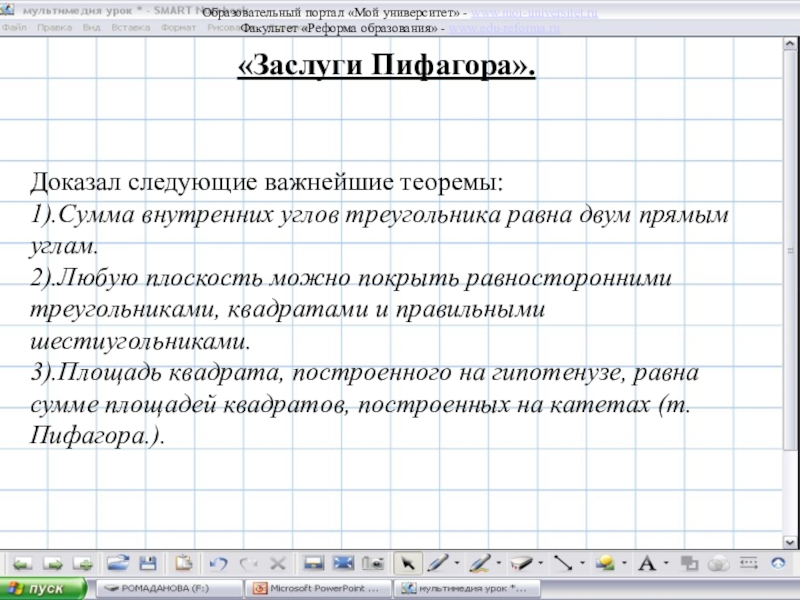
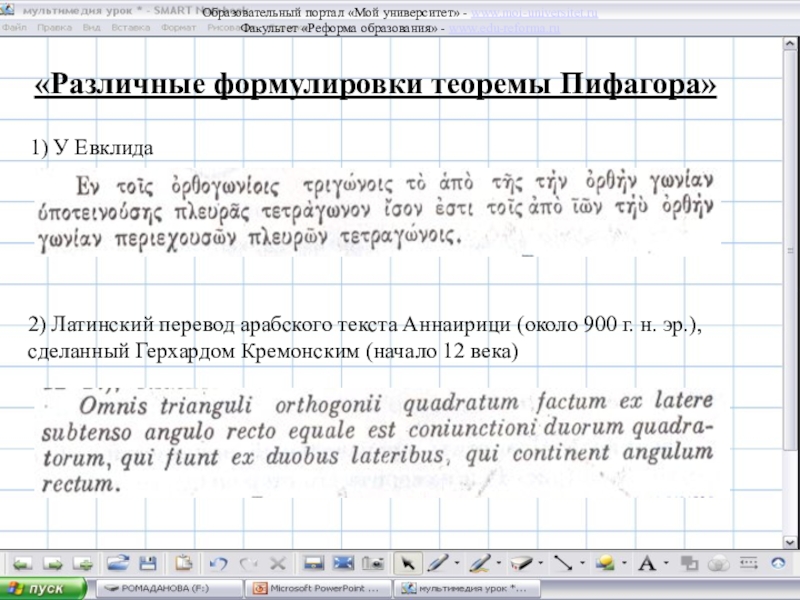
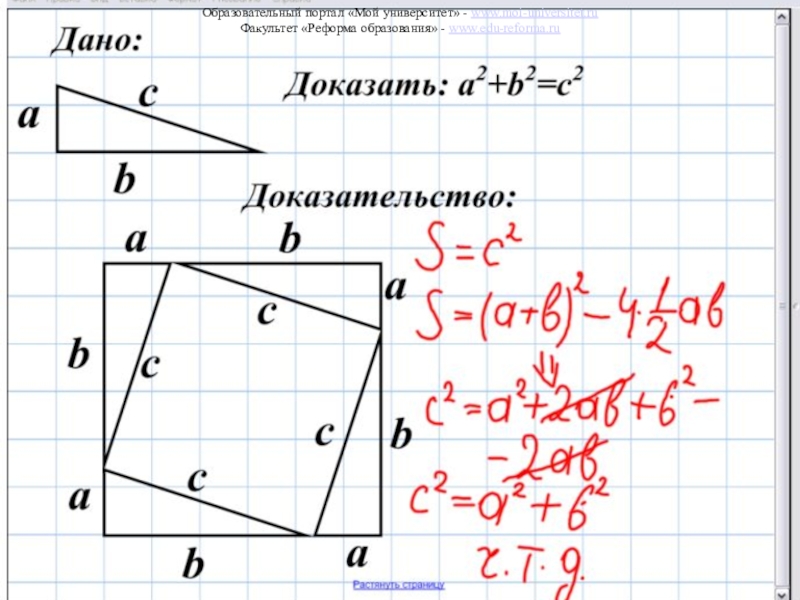
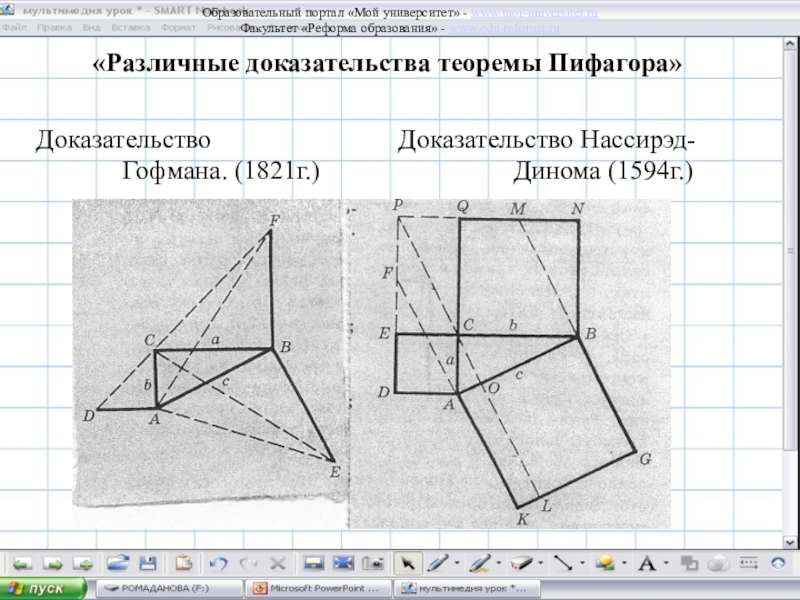
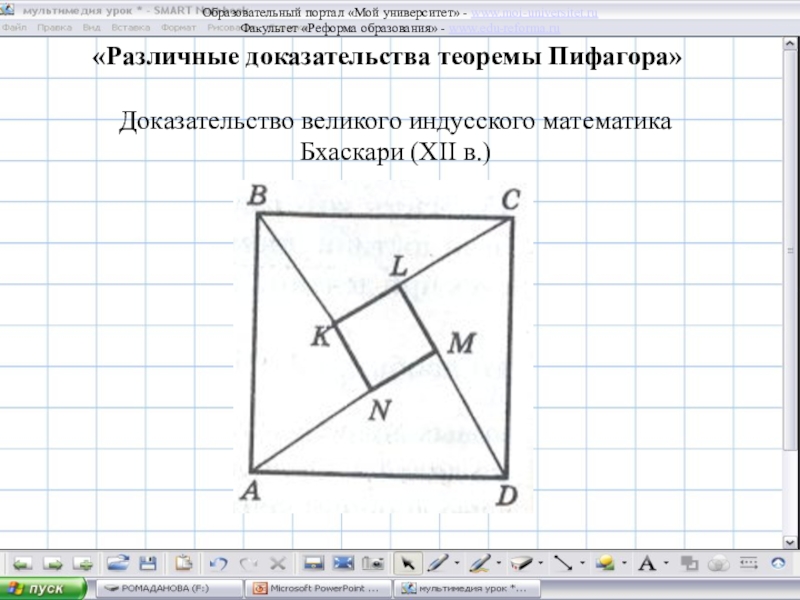
одно из них – это теорема Пифагора, а
другое – деление отрезка в среднем и
крайнем отношении… Первое можно
сравнить с мерой золота; второй же больше
напоминает драгоценный камень».
Иоганн Кеплер

Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

Теорема Пифагора: с древнейших времен до наших дней«Геометрия владеет двумя сокровищами: одно из них –

Слайд 2
Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования» - www.edu-reforma.ru

Слайд 3На берегу реки рос тополь одинокий.
Вдруг порыв ветра его ствол надломил.


Бедный тополь упал.
И угол прямой с теченьем реки его ствол составлял.
Запомни теперь, что в том месте река,
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?

Задачи из древнего мира.

Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

На берегу реки рос тополь одинокий.Вдруг порыв ветра его ствол надломил. Бедный тополь упал. И угол прямой

Слайд 4Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования» - www.edu-reforma.ru

Слайд 5«Заслуги Пифагора».

Доказал следующие важнейшие теоремы:
1).Сумма внутренних углов треугольника равна двум прямым

углам.
2).Любую плоскость можно покрыть равносторонними треугольниками, квадратами и правильными шестиугольниками.
3).Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах (т. Пифагора.).

Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

«Заслуги Пифагора».Доказал следующие важнейшие теоремы:1).Сумма внутренних углов треугольника равна двум прямым углам.2).Любую плоскость можно покрыть равносторонними треугольниками,

Слайд 6«Различные формулировки теоремы Пифагора»

1) У Евклида
2) Латинский перевод арабского текста Аннаирици

(около 900 г. н. эр.), сделанный Герхардом Кремонским (начало 12 века)


Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

«Различные формулировки теоремы Пифагора»1) У Евклида2) Латинский перевод арабского текста Аннаирици (около 900 г. н. эр.), сделанный

Слайд 7«Различные формулировки теоремы Пифагора»

3) В Geometric Culmonensis(около 1400

г.)


4) В первом русском переводе евклидовых «Начал», сделанном с греческого Ф.И.Петрушевским

«В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол».

Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

«Различные формулировки теоремы Пифагора» 3) В Geometric Culmonensis(около 1400 г.) 4) В первом русском переводе

Слайд 8 «Если дан

нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путём
К результату мы придём».

5) В стихотворной форме

«Различные формулировки теоремы Пифагора»

Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

«Если дан нам треугольник

Слайд 9Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования» - www.edu-reforma.ru

Слайд 10«Различные доказательства теоремы Пифагора»

Египетский треугольник со сторонами 3,4,5.
Его, по другому, называют

веревочный треугольник.
Им пользовались в Древнем Египте
для построения прямых углов на местности.

Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

«Различные доказательства теоремы Пифагора»Египетский треугольник со сторонами 3,4,5.Его, по другому, называют веревочный треугольник. Им пользовались в Древнем

Слайд 11«Различные доказательства теоремы Пифагора»
Чертеж к теореме Пифагора в арабской рукописи.

Образовательный портал

«Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

«Различные доказательства теоремы Пифагора»Чертеж к теореме Пифагора в арабской рукописи.Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования»

Слайд 12«Различные доказательства теоремы Пифагора»
ДоказательствоЕвклида в «Началах».

Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет

«Реформа образования» - www.edu-reforma.ru

«Различные доказательства теоремы Пифагора»ДоказательствоЕвклида в «Началах».Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования» - www.edu-reforma.ru

Слайд 13Доказательство Энштейна. Доказательство ан-Найризия.


«Различные доказательства теоремы Пифагора»


Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

Доказательство Энштейна. Доказательство ан-Найризия.

Слайд 14«Различные доказательства теоремы Пифагора»
А это принадлежит лондонскому биржевому маклеру и астроному

– любителю Генри Периэлу.


Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

«Различные доказательства теоремы Пифагора»А это принадлежит лондонскому биржевому маклеру и астроному – любителю Генри Периэлу.Образовательный портал «Мой

Слайд 15«Различные доказательства теоремы Пифагора»
Доказательство

Доказательство Нассирэд-
Гофмана. (1821г.) Динома (1594г.)


Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

«Различные доказательства теоремы Пифагора»Доказательство

Слайд 16Доказательство Гарфилда
«Различные доказательства теоремы Пифагора»
Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа

образования» - www.edu-reforma.ru

Доказательство Гарфилда«Различные доказательства теоремы Пифагора»Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования» - www.edu-reforma.ru

Слайд 17«Различные доказательства теоремы Пифагора»
Доказательство великого индусского математика Бхаскари (XII в.)
Образовательный портал

«Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

«Различные доказательства теоремы Пифагора»Доказательство великого индусского математика Бхаскари (XII в.)Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования»

Слайд 18Доказательство в Древней Индии приводимое без слов только «Смотри».
«Различные доказательства

теоремы Пифагора»


Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

Доказательство в Древней Индии приводимое без слов только «Смотри». «Различные доказательства теоремы Пифагора»Образовательный портал «Мой университет» -

Слайд 19Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования» - www.edu-reforma.ru

Слайд 20Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования» - www.edu-reforma.ru

Слайд 21Самостоятельная работа

Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» -

www.edu-reforma.ru

Самостоятельная работа Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования» - www.edu-reforma.ru

Слайд 22Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

Образовательный портал «Мой университет» - www.moi-universitet.ruФакультет «Реформа образования» - www.edu-reforma.ru

Слайд 23 Домашнее задание.

Найти или придумать задачу с практическим применением.

Задачу и ее решение оформить в программе POWER POINT для презентации на следующем уроке.

Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

Домашнее задание. Найти или придумать задачу с практическим применением. Задачу и ее решение оформить в
Скачать презентацию

Похожие презентации

Теоретический материал по планиметрии 7-9 классы Теоретический материал по планиметрии 7-9 классы 202
Презентация по геометрии Первый признак равенства треугольников Презентация по геометрии Первый признак равенства треугольников 222
Проект по инновационной деятельности на тему: Геометрические термины и символы. Проект по инновационной деятельности на тему: Геометрические термины и символы. 247
Приложение к уроку Прямоугольный треугольник Приложение к уроку Прямоугольный треугольник 247
Презентация по геометрии На тему Соотношения между сторонами и углами в прямоугольном треугольнике (8 класс) Презентация по геометрии На тему Соотношения между сторонами и углами в прямоугольном треугольнике (8 класс) 230
Медиана, биссектриса, высота Медиана, биссектриса, высота 251

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Яндекс.Метрика

Обратная связь

Email: Нажмите что бы посмотреть