Пахомова О.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теорема Пифагора
Содержание
- 1. Теорема Пифагора
- 2. Теорема Пифагора: Сумма площадей квадратов, опирающихся на
- 3. Обе формулировки теоремы эквивалентны, но вторая формулировка
- 4. Пусть ABC есть прямоугольный треугольник с прямым
- 5. Часто бывают случаи, когда ученики помнят формулировку
- 6. Теорема Пифагора – одна из главных теорем
- 7. Решение задач, в которых применяется теорема Пифагора.Задача
- 8. Задача 2Решение. ∆DCE - прямоугольный с
- 9. Задача 3Решение.∠KLM вписан в окружность и опирается
- 10. Задача 4 Высота, опущенная из вершины В
Теорема Пифагора: Сумма площадей квадратов, опирающихся на катеты (a и b), равна площади квадрата, построенного на гипотенузе (c).Геометрическая формулировка:Изначально теорема была сформулирована следующим образом: В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов,
Слайд 2Теорема Пифагора: Сумма площадей квадратов, опирающихся на катеты (a и b),
равна площади квадрата, построенного на гипотенузе (c).
Геометрическая формулировка:
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Алгебраическая формулировка:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы
треугольника через c, а длины катетов
через a и b:
a2 + b2 = c2
Геометрическая формулировка:
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Алгебраическая формулировка:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы
треугольника через c, а длины катетов
через a и b:
a2 + b2 = c2
Слайд 3Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не
требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.
Обратная теорема Пифагора:
Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Доказательства:
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Обратная теорема Пифагора:
Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Доказательства:
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Слайд 4Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту
из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам.
Аналогично, треугольник CBH подобен ABC.
Введя обозначения
Получаем:
Аналогично, треугольник CBH подобен ABC.
Введя обозначения
Получаем:
.
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим -
И таким простым путём
К результату мы придём
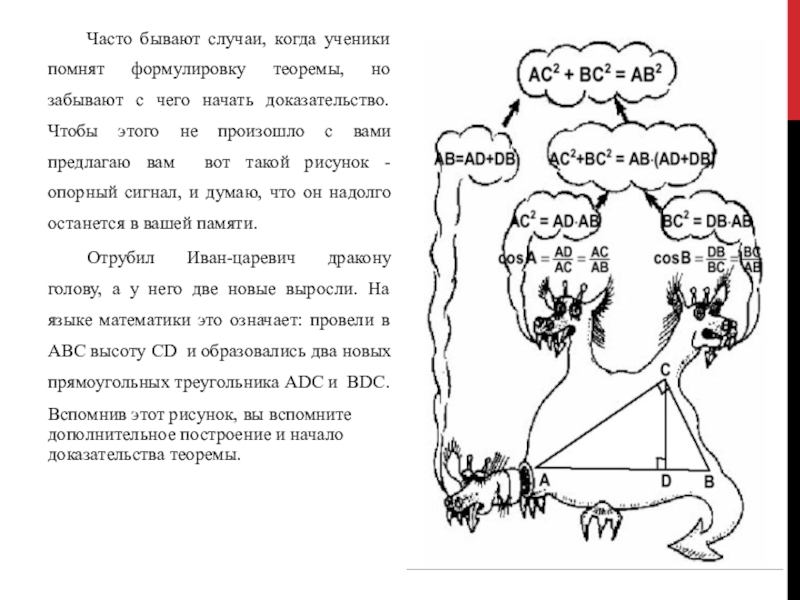
Слайд 5Часто бывают случаи, когда ученики помнят формулировку теоремы, но забывают с
чего начать доказательство. Чтобы этого не произошло с вами предлагаю вам вот такой рисунок - опорный сигнал, и думаю, что он надолго останется в вашей памяти.
Отрубил Иван-царевич дракону голову, а у него две новые выросли. На языке математики это означает: провели в ABC высоту CD и образовались два новых прямоугольных треугольника ADC и BDC.
Вспомнив этот рисунок, вы вспомните дополнительное построение и начало доказательства теоремы.
Отрубил Иван-царевич дракону голову, а у него две новые выросли. На языке математики это означает: провели в ABC высоту CD и образовались два новых прямоугольных треугольника ADC и BDC.
Вспомнив этот рисунок, вы вспомните дополнительное построение и начало доказательства теоремы.
Слайд 6Теорема Пифагора – одна из главных теорем геометрии, потому что с
её помощью доказывается много других теорем и решается множество задач.
Особенностью теоремы Пифагора является то, что она неочевидна. Например, свойства равнобедренного треугольника можно увидеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что его стороны находятся в соотношении
Особенностью теоремы Пифагора является то, что она неочевидна. Например, свойства равнобедренного треугольника можно увидеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что его стороны находятся в соотношении
Слайд 7Решение задач, в которых применяется теорема Пифагора.
Задача 1
Решение.
∆АВС – прямоугольный с
гипотенузой АВ,
по теореме Пифагора: АВ2 = АС2 + ВС2,
АВ2 = 82 + 62,
АВ2 = 64 + 36,
АВ2 = 100,
АВ = √100,
АВ = 10.
Замечание: Из курса алгебры известно, что уравнение АВ2 = 100 имеет два корня АВ = + √100. АВ = -10 не удовлетворяет условию задачи, так как длина стороны треугольника всегда положительна. Значит АВ = 10. В дальнейшем при решении уравнений в подобных задачах, мы будем находить только положительные корни, и не будем объяснять каждый раз, почему отрицательные корни отбрасываются.
по теореме Пифагора: АВ2 = АС2 + ВС2,
АВ2 = 82 + 62,
АВ2 = 64 + 36,
АВ2 = 100,
АВ = √100,
АВ = 10.
Замечание: Из курса алгебры известно, что уравнение АВ2 = 100 имеет два корня АВ = + √100. АВ = -10 не удовлетворяет условию задачи, так как длина стороны треугольника всегда положительна. Значит АВ = 10. В дальнейшем при решении уравнений в подобных задачах, мы будем находить только положительные корни, и не будем объяснять каждый раз, почему отрицательные корни отбрасываются.
Слайд 8Задача 2
Решение.
∆DCE - прямоугольный с гипотенузой DE,
по теореме
Пифагора: DE2 = DC2 + CE2,
DC2 = DE2 – CE2,
DC2 = 52 – 32,
DC2 = 25 – 9,
DC2 = 16,
DC = 4.
Мы с вами получили треугольник со сторонами 3, 4 и 5 единиц. Это единственный прямоугольный треугольник стороны которого равны трём последовательным натуральным числам. Его часто называют египетским треугольником, так как он был известен ещё древним египтянам. Они использовали этот треугольник в «правиле верёвки» для построения прямых углов при закладке зданий, храмов, алтарей и т.п.
DC2 = DE2 – CE2,
DC2 = 52 – 32,
DC2 = 25 – 9,
DC2 = 16,
DC = 4.
Мы с вами получили треугольник со сторонами 3, 4 и 5 единиц. Это единственный прямоугольный треугольник стороны которого равны трём последовательным натуральным числам. Его часто называют египетским треугольником, так как он был известен ещё древним египтянам. Они использовали этот треугольник в «правиле верёвки» для построения прямых углов при закладке зданий, храмов, алтарей и т.п.
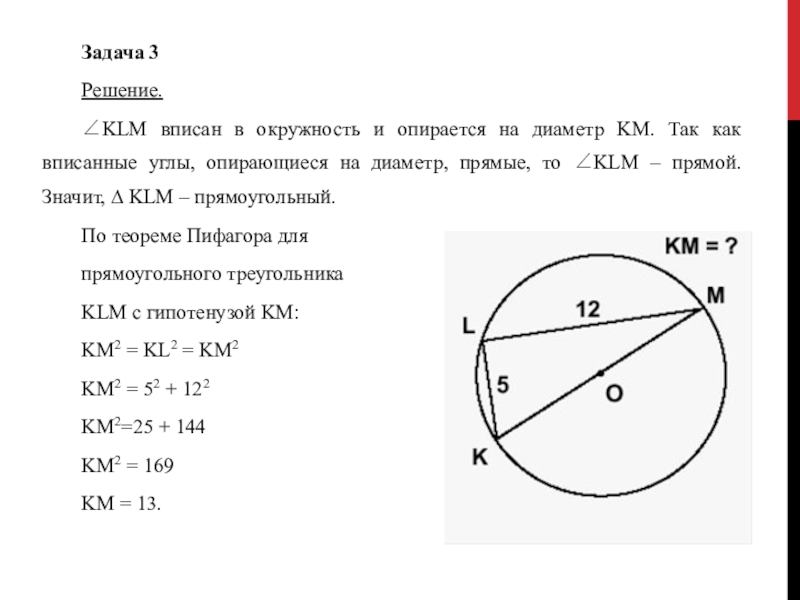
Слайд 9Задача 3
Решение.
∠KLM вписан в окружность и опирается на диаметр KM. Так
как вписанные углы, опирающиеся на диаметр, прямые, то ∠KLM – прямой. Значит, ∆ KLM – прямоугольный.
По теореме Пифагора для
прямоугольного треугольника
KLM с гипотенузой KM:
KM2 = KL2 = KM2
KM2 = 52 + 122
KM2=25 + 144
KM2 = 169
KM = 13.
По теореме Пифагора для
прямоугольного треугольника
KLM с гипотенузой KM:
KM2 = KL2 = KM2
KM2 = 52 + 122
KM2=25 + 144
KM2 = 169
KM = 13.
Слайд 10Задача 4
Высота, опущенная из вершины В АВС, делит сторону АС
на отрезки, равные 16 см. и 9 см. Найдите сторону ВС, если сторона АВ равна 20 см
Дано: ∆АВС, BD ┴ AC , АВ = 20 см, AD = 16 см, DC = 9 см.
Найти: ВС.
Решение. По условию задачи BD ┴ AC, значит, ∆ABD и ∆CBD – прямоугольные. По теореме Пифагора для ∆ ABD: AB2 = AD2 + BD2, отсюда
BD2 = AB2 - AD2,
BD2 = 202 – 162,
BD2 = 400 – 256,
BD2 = 144,
BD = 12см.
По теореме Пифагора для ∆CBD:
BC2 = BD2 + DC2, отсюда BC2 = 122 + 92, BC2 = 144 + 81,
BC2 = 225, BC = 15см.
Ответ: BC = 15 см.
Замечание: На втором этапе решения достаточно было найти BD и подставить его значение в равенство BC = BD +DC .
Дано: ∆АВС, BD ┴ AC , АВ = 20 см, AD = 16 см, DC = 9 см.
Найти: ВС.
Решение. По условию задачи BD ┴ AC, значит, ∆ABD и ∆CBD – прямоугольные. По теореме Пифагора для ∆ ABD: AB2 = AD2 + BD2, отсюда
BD2 = AB2 - AD2,
BD2 = 202 – 162,
BD2 = 400 – 256,
BD2 = 144,
BD = 12см.
По теореме Пифагора для ∆CBD:
BC2 = BD2 + DC2, отсюда BC2 = 122 + 92, BC2 = 144 + 81,
BC2 = 225, BC = 15см.
Ответ: BC = 15 см.
Замечание: На втором этапе решения достаточно было найти BD и подставить его значение в равенство BC = BD +DC .