- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Технология решения геометрических задач на уроках в 10-11 классах при подготовке к ЕГЭ
Содержание
- 1. Технология решения геометрических задач на уроках в 10-11 классах при подготовке к ЕГЭ
- 2. Биссектриса угла в треугольнике делит противоположную сторону
- 3. Задачи1) В прямоугольном треугольнике АВЕ с прямым
- 4. Свойство четырехугольника, описанного около окружности, и четырехугольника,
- 5. Технология решения планиметрических задач по геометрии на
- 6. Программа по планиметрии
- 7. Этапы блока1 этап – повторение необходимых теоретических
- 8. Площади многоугольниковРешение задач на готовых чертежах
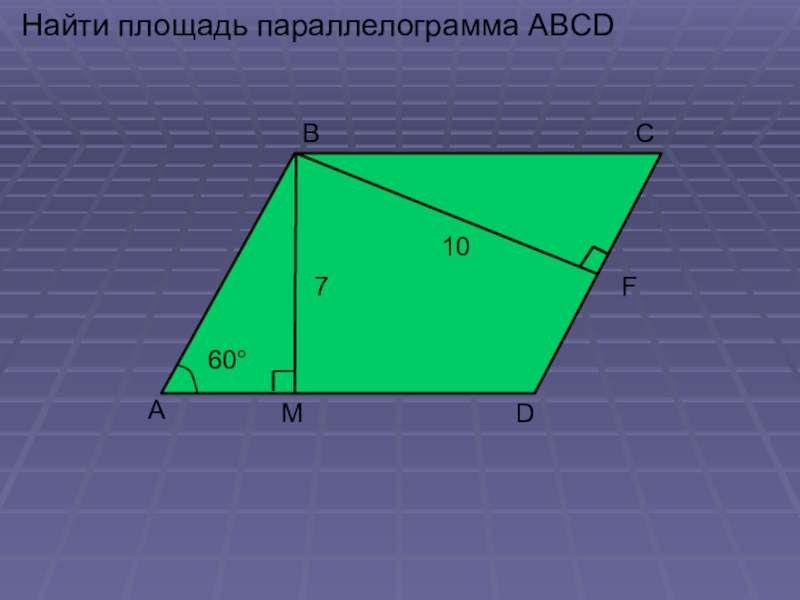
- 9. Найти площадь параллелограмма ABCD
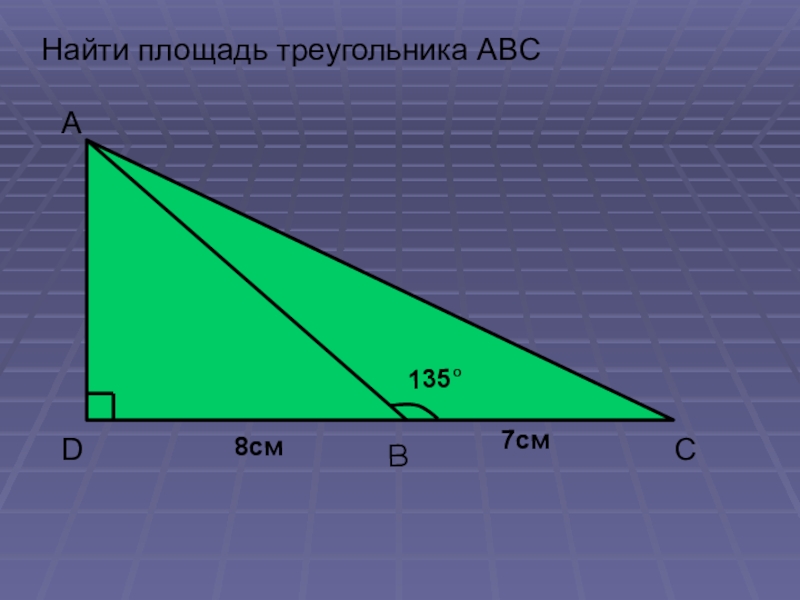
- 10. Найти площадь треугольника ABC
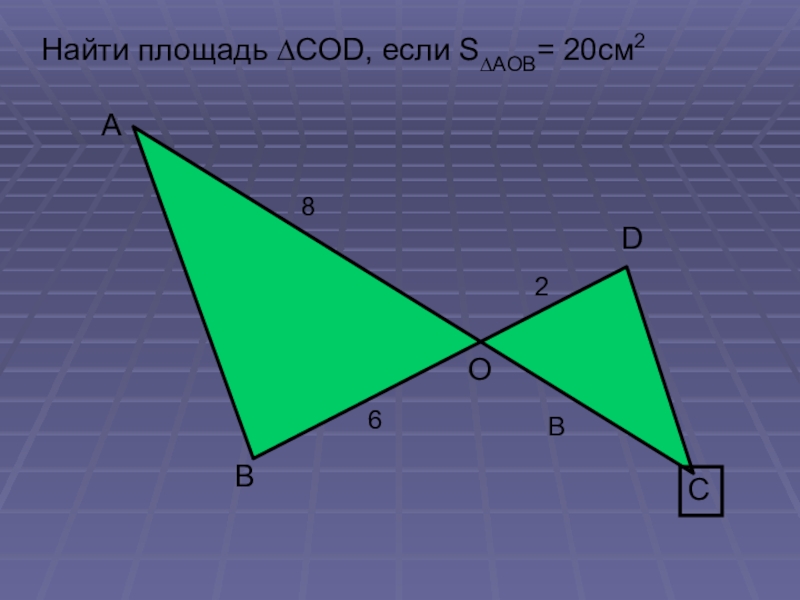
- 11. Найти площадь ∆COD, если S∆AOB= 20см2
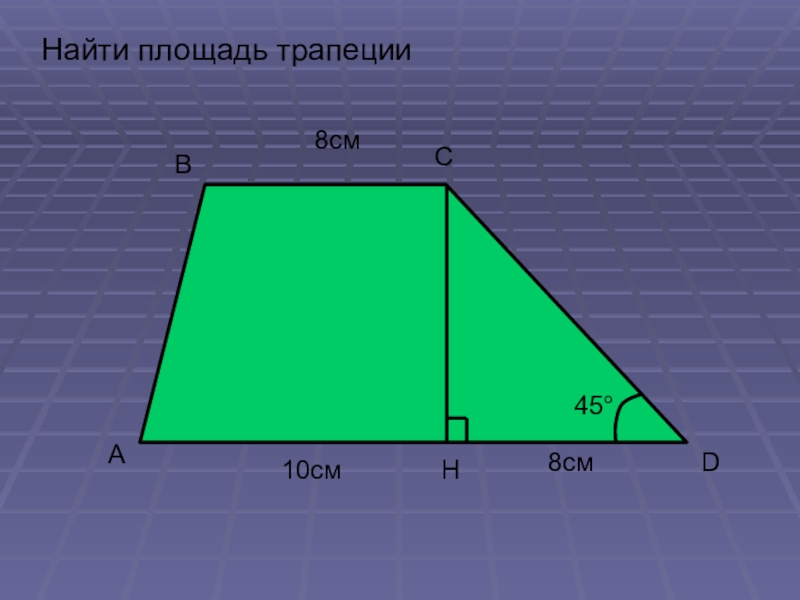
- 12. Найти площадь трапеции
- 13. Пример практического варианта домашней контрольной работы по
- 14. 7. Одна сторона прямоугольника на 2 см
- 15. Пример практического варианта домашней контрольной работы по
- 16. Учебный процесс должен
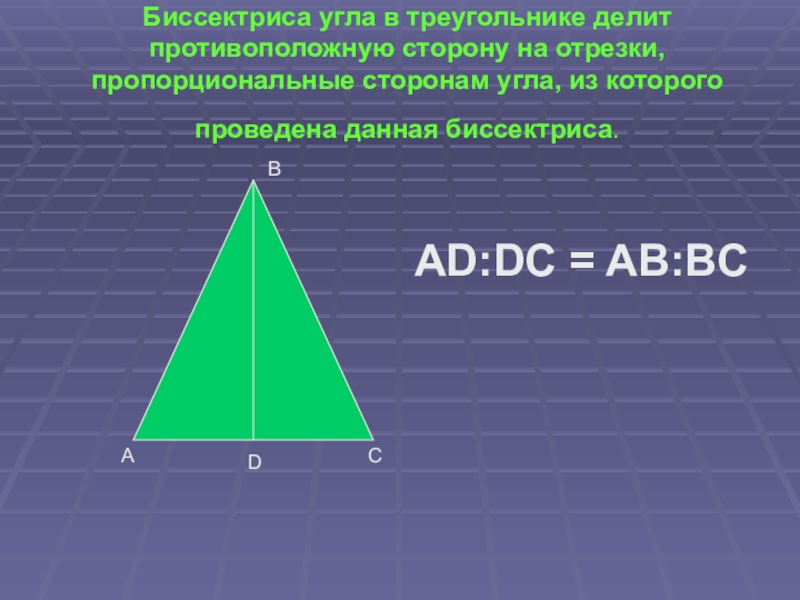
Биссектриса угла в треугольнике делит противоположную сторону на отрезки, пропорциональные сторонам угла, из которого проведена данная биссектриса. AD:DC = AB:BCАСВD
Слайд 2Биссектриса угла в треугольнике делит противоположную сторону на отрезки, пропорциональные сторонам
угла, из которого проведена данная биссектриса.
AD:DC = AB:BC
А
С
В
D
Слайд 3Задачи
1) В прямоугольном треугольнике АВЕ с прямым углом Е проведена биссектриса
ВТ, причем АТ = 15, ТЕ = 12. Найдите площадь треугольника АВТ.
2) В прямоугольном треугольнике АВС с прямым углом С проведена биссектриса ВК. Найдите площадь треугольника АВК, если площадь треугольника АВС равна 21, а синус угла А равна 0,4.
2) В прямоугольном треугольнике АВС с прямым углом С проведена биссектриса ВК. Найдите площадь треугольника АВК, если площадь треугольника АВС равна 21, а синус угла А равна 0,4.
Слайд 4Свойство четырехугольника, описанного около окружности, и четырехугольника, вписанного в окружность
У
четырехугольника, в который вписана окружность, суммы противоположных сторон равны.
У четырехугольника, около которого описана окружность, сумма противоположных углов равна 180 градусам.
У четырехугольника, около которого описана окружность, сумма противоположных углов равна 180 градусам.
Слайд 5Технология решения планиметрических задач по геометрии на уроках в 10–11-х классах
сформировать
целостное понятие геометрии на плоскости;
повысить мотивацию изучения геометрии;
повысить качество знаний;
повысить уровень образовательного процесса в целом.
повысить мотивацию изучения геометрии;
повысить качество знаний;
повысить уровень образовательного процесса в целом.
Слайд 7Этапы блока
1 этап – повторение необходимых теоретических знаний;
2 этап – решение
простейших задач и контроль в группах и в парах; работа по дидактическому материалу;
3 этап – решение нестандартных и трудных задач;
4 этап – предварительный контроль;
5 этап – домашняя контрольная работа.
3 этап – решение нестандартных и трудных задач;
4 этап – предварительный контроль;
5 этап – домашняя контрольная работа.
Слайд 13Пример практического варианта домашней контрольной работы по планиметрии
Вариант 1
1. Угол
ВАС при основании АВ равнобедренного треугольника АВС равен 50o. Высоты треугольника пересекаются в точке О.
Вычислить АОВ.
2. Высота равностороннего треугольника равна 5 см. На одной из его сторон дана точка, расстояние от которой до другой стороны равно 3 см. Найти расстояние от этой точки до другой стороны.
3. Сумма двух углов параллелограмма равна 100o. Вычислите углы параллелограмма.
4. Острый угол прямоугольной трапеции равен 45o. Определить ее среднюю линию, если меньшая диагональ и большая боковая сторона равны между собой и меньшее основание равно 12 см.
5. Средняя линия равнобедренной трапеции равна 18 см, отношение оснований равно 1 : 5. Определить высоту трапеции, если ее боковая сторона равна 15 см.
6. Сумма длин диагоналей квадрата равна 16 см. Найти площадь прямоугольника, если одна его сторона на 3 см меньше другой, а периметр равен периметру квадрата.
2. Высота равностороннего треугольника равна 5 см. На одной из его сторон дана точка, расстояние от которой до другой стороны равно 3 см. Найти расстояние от этой точки до другой стороны.
3. Сумма двух углов параллелограмма равна 100o. Вычислите углы параллелограмма.
4. Острый угол прямоугольной трапеции равен 45o. Определить ее среднюю линию, если меньшая диагональ и большая боковая сторона равны между собой и меньшее основание равно 12 см.
5. Средняя линия равнобедренной трапеции равна 18 см, отношение оснований равно 1 : 5. Определить высоту трапеции, если ее боковая сторона равна 15 см.
6. Сумма длин диагоналей квадрата равна 16 см. Найти площадь прямоугольника, если одна его сторона на 3 см меньше другой, а периметр равен периметру квадрата.
Слайд 14
7. Одна сторона прямоугольника на 2 см меньше другой, а его
площадь равна 35. Найти площадь квадрата, периметр которого равен периметру данного прямоугольника.
8. Найти площадь равнобедренного треугольника, если высоты, опущенные на его основание и боковую сторону, соответственно равны 5 и 6.
9. Диагонали равнобочной трапеции взаимно перпендикулярны, а площадь равна 4. Определить высоту трапеции.
10. Около окружности описана равнобедренная трапеция с тупым углом 120o и периметром 36. Найти ее площадь.
11. В равнобедренном треугольнике основание равно 30, а боковая сторона – 39. Определить радиус вписанной окружности.
12. В равнобочную трапецию, площадь которой равна 20, вписана окружность радиуса 2. Определить стороны трапеции.
13. В параллелограмме острый угол равен 60o. Найти стороны параллелограмма, если его периметр равен 22, а меньшая диагональ равна 7.
14. В трапеции АВСД Д=АСВ. АС – биссектриса угла А. Определить диагональ АС, если средняя линия трапеции равна 8, а основания относятся как 3: 5.
8. Найти площадь равнобедренного треугольника, если высоты, опущенные на его основание и боковую сторону, соответственно равны 5 и 6.
9. Диагонали равнобочной трапеции взаимно перпендикулярны, а площадь равна 4. Определить высоту трапеции.
10. Около окружности описана равнобедренная трапеция с тупым углом 120o и периметром 36. Найти ее площадь.
11. В равнобедренном треугольнике основание равно 30, а боковая сторона – 39. Определить радиус вписанной окружности.
12. В равнобочную трапецию, площадь которой равна 20, вписана окружность радиуса 2. Определить стороны трапеции.
13. В параллелограмме острый угол равен 60o. Найти стороны параллелограмма, если его периметр равен 22, а меньшая диагональ равна 7.
14. В трапеции АВСД Д=АСВ. АС – биссектриса угла А. Определить диагональ АС, если средняя линия трапеции равна 8, а основания относятся как 3: 5.
Слайд 15Пример практического варианта домашней контрольной работы по стереометрии
Вариант
1
1. Радиус основания цилиндра равен 6, а высота равна 2. Отрезки AB и CD – диаметры одного из оснований цилиндра, а отрезок АА – его образующая. Известно, что ВС= 2√21. Найдите синус угла между прямыми АС и BD.
2. Радиус основания цилиндра равен 4, а высота равна 9. Отрезок АВ и СD – диаметры одного из оснований цилиндра, а отрезок АА1 - его образующая. Известно, что ВС = 1. Найдите синус угла между прямыми А1С и ВD.
3. Угол между образующими СА и СВ конуса равен 60˚, высота
конуса равна 4, образующая равна. Найдите расстояние от центра основания конуса до плоскости АВС
4. Угол между образующими СА и СВ конуса равен 120 градусов, высота конуса равна 5, а образующая равна 12,5. Найдите расстояние от центра основания конуса до плоскости АВС
5. Угол между образующими СА и CD конуса равен 90˚, высота конуса равна6, а образующая равна 4. Найдите расстояние от центра основания конуса до плоскости АВС.
6. Угол между образующими СА и СВ конуса равен 60˚, высота
конуса равна 5, образующая равна . Найдите расстояние от центра основания конуса до плоскости АВС
1. Радиус основания цилиндра равен 6, а высота равна 2. Отрезки AB и CD – диаметры одного из оснований цилиндра, а отрезок АА – его образующая. Известно, что ВС= 2√21. Найдите синус угла между прямыми АС и BD.
2. Радиус основания цилиндра равен 4, а высота равна 9. Отрезок АВ и СD – диаметры одного из оснований цилиндра, а отрезок АА1 - его образующая. Известно, что ВС = 1. Найдите синус угла между прямыми А1С и ВD.
3. Угол между образующими СА и СВ конуса равен 60˚, высота
конуса равна 4, образующая равна. Найдите расстояние от центра основания конуса до плоскости АВС
4. Угол между образующими СА и СВ конуса равен 120 градусов, высота конуса равна 5, а образующая равна 12,5. Найдите расстояние от центра основания конуса до плоскости АВС
5. Угол между образующими СА и CD конуса равен 90˚, высота конуса равна6, а образующая равна 4. Найдите расстояние от центра основания конуса до плоскости АВС.
6. Угол между образующими СА и СВ конуса равен 60˚, высота
конуса равна 5, образующая равна . Найдите расстояние от центра основания конуса до плоскости АВС
Слайд 16
Учебный процесс должен быть организован так, чтобы
все учащиеся освоили материал курса на обязательном уровне и, кроме того, чтобы обучение способствовало удовлетворению потребностей и запросов школьников, проявляющих интерес, склонности и способности к математике. Такие школьники должны получать индивидуальные задания (и в первую очередь нестандартные математические задачи), их следует привлекать к участию в математических кружках, олимпиадах, факультативных занятиях; желательно рекомендовать им дополнительную литературу.
(Программа по математике для средней школы)
(Программа по математике для средней школы)