- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Симметрия в пространстве. Презентация по математике
Содержание
- 1. Симметрия в пространстве. Презентация по математике
- 2. Точки А и А1 называются симметричными относительно
- 3. Точки А и А1 называются симметричными относительно
- 4. Точки А и А1 называются симметричными относительно
- 5. Точка (прямая, плоскость) называется центром (осью, плоскостью)
- 6. На рисунках показаны центр О, ось а
- 7. Фигура может иметь один или несколько центров
- 8. С симметрией мы часто сталкиваемся в природе, технике, архитектуре, быту.
- 9. В геометрии центр, оси и плоскости симметрии многогранника называются элементами симметрии этого многогранника
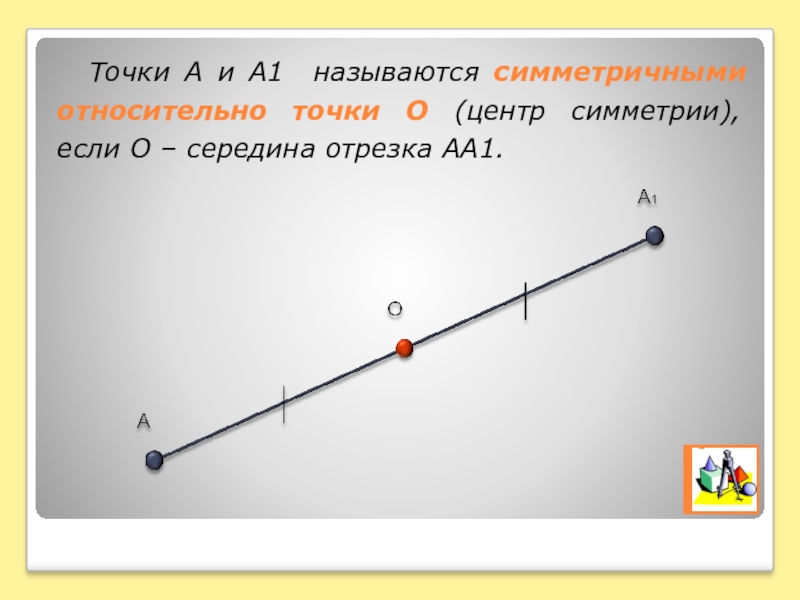
Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА1.
Слайд 2Точки А и А1 называются симметричными относительно точки О (центр симметрии),
если О – середина отрезка АА1.
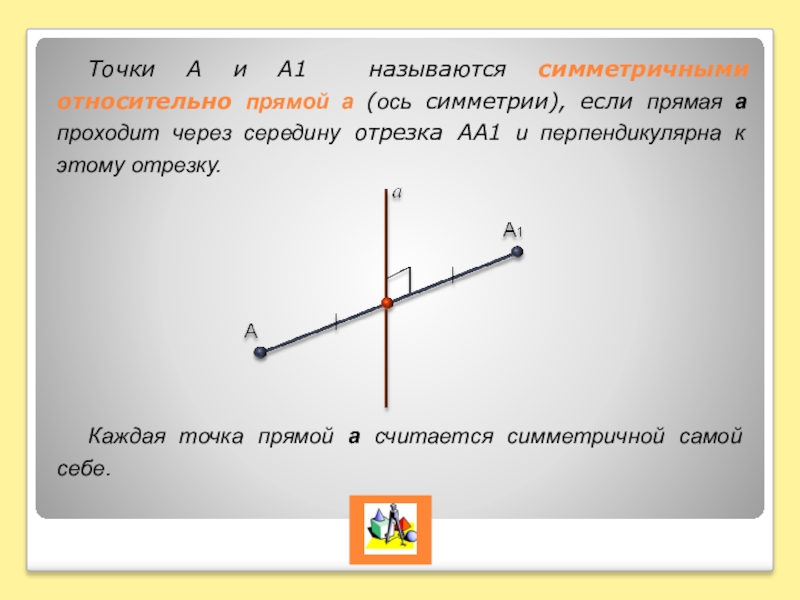
Слайд 3Точки А и А1 называются симметричными относительно прямой а (ось симметрии),
если прямая а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку.
Каждая точка прямой а считается симметричной самой себе.
Каждая точка прямой а считается симметричной самой себе.
Слайд 4
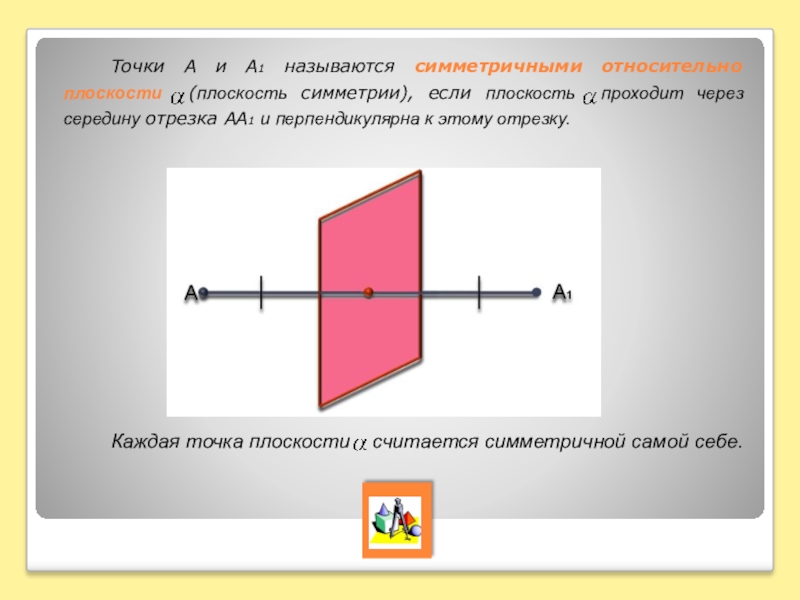
Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии), если
плоскость проходит через середину отрезка АА1 и перпендикулярна к этому отрезку.
Каждая точка плоскости считается симметричной самой себе.
Каждая точка плоскости считается симметричной самой себе.
Слайд 5Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая
точка фигуры симметрична относительно нее некоторой точке той же фигуры.
Слайд 6
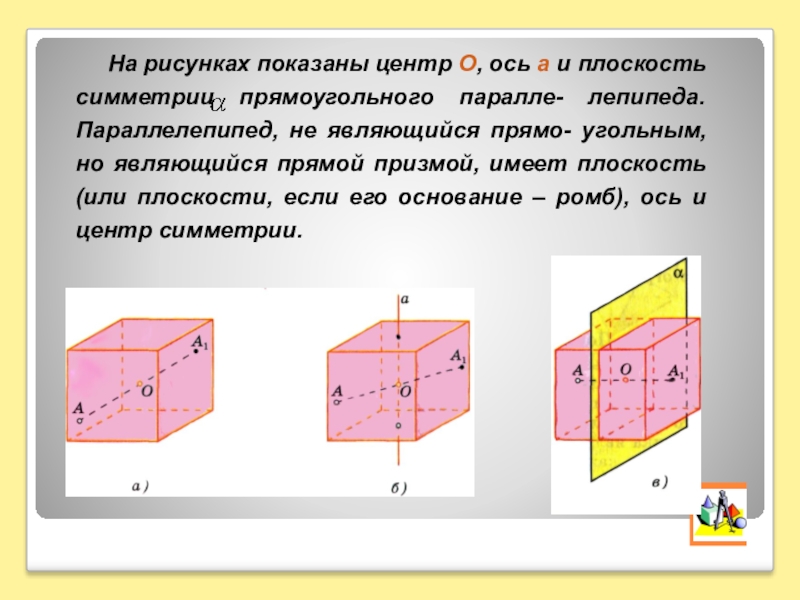
На рисунках показаны центр О, ось а и плоскость симметрии прямоугольного
паралле- лепипеда. Параллелепипед, не являющийся прямо- угольным, но являющийся прямой призмой, имеет плоскость (или плоскости, если его основание – ромб), ось и центр симметрии.
Слайд 7Фигура может иметь один или несколько центров симметрии (осей, плоскостей симметрии)
– куб. Существуют фигуры, имеющие бесконечно много центров, осей или плоскостей симметрии - прямая или плоскость. Так же существуют фигуры, не имеющие центров, осей или плоскостей симметрии – параллелепипед, призма, пирамида.
Слайд 9В геометрии центр, оси и плоскости симметрии многогранника называются элементами симметрии
этого многогранника