- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Симметрия на плоскости
Содержание
- 1. Симметрия на плоскости
- 2. СОДЕРЖАНИЕ1)Определение симметрии 2)Виды симметрии 3)Симметрия относительно
- 3. Симметрия, в широком смысле — соответствие, неизменность (инвариантность),
- 4. ВИДЫ СИММЕТРИИ ✔Центральная симметрия ✔Осевая (зеркальная) симметрия ✔Поворотная симметрия ✔Параллельный перенос
- 5. Слайд 5
- 6. Слайд 6
- 7. ЦЕНТРАЛЬНАЯ СИММЕТРИЯЦентральной симметрией относительно точки A называют преобразование
- 8. ОСЕВАЯ СИММЕТРИЯ Вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии
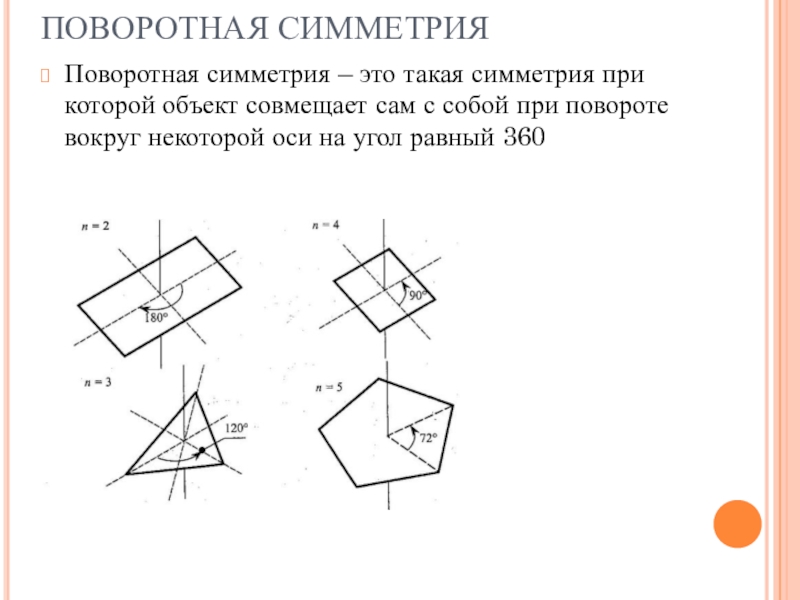
- 9. ПОВОРОТНАЯ СИММЕТРИЯПоворотная симметрия – это такая симметрия
- 10. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСНаглядно параллельный перенос определяется как преобразование, при котором
- 11. ОСЬ СИММЕТРИИОсь симметрии – воображаемая ось, при повороте
- 12. ЦЕНТР СИММЕТРИИЦентр симметрии – это точка внутри кристалла,
- 13. Зеркальная симметрия или отражение — движение пространства, множество неподвижных
- 14. ВИНТОВАЯ СИММЕТРИЯОСЬ СИММЕТРИИ ВИНТОВАЯ — элемент симметрии бесконечных
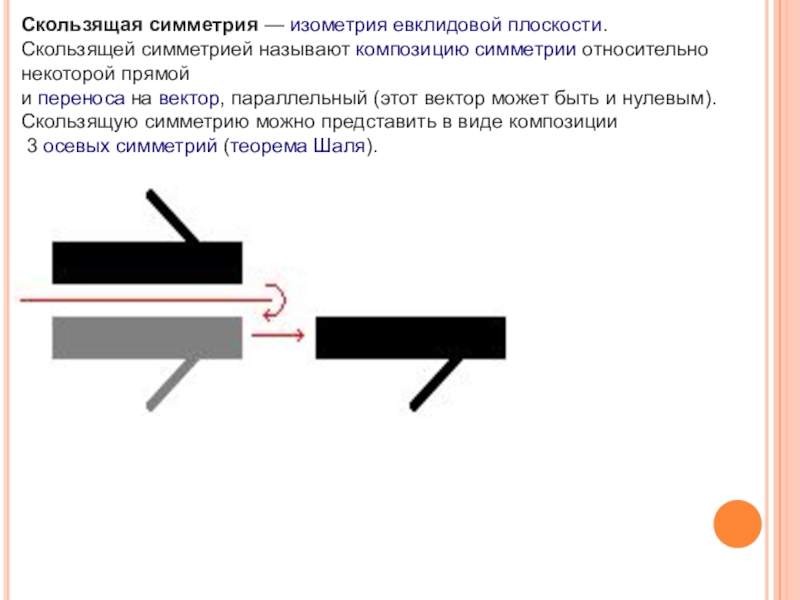
- 15. Скользящая симметрия — изометрия евклидовой плоскости.Скользящей симметрией называют композицию симметрии относительно
- 16. СПАСИБО ЗА ВНИМАНИЕ.
СОДЕРЖАНИЕ1)Определение симметрии 2)Виды симметрии 3)Симметрия относительно плоскости 4)Определение Центральной симметрии 5)Определение Осевой симметрии 6)Определение Поворотной симметрии 7)Параллельный перенос 8)Определение Оси симметрии 9)Определение Центр симметрии 10)Зеркальная симметрия 11)Винтовая ось симметрии 12)Скользящая симметрия
Слайд 2СОДЕРЖАНИЕ
1)Определение симметрии
2)Виды симметрии
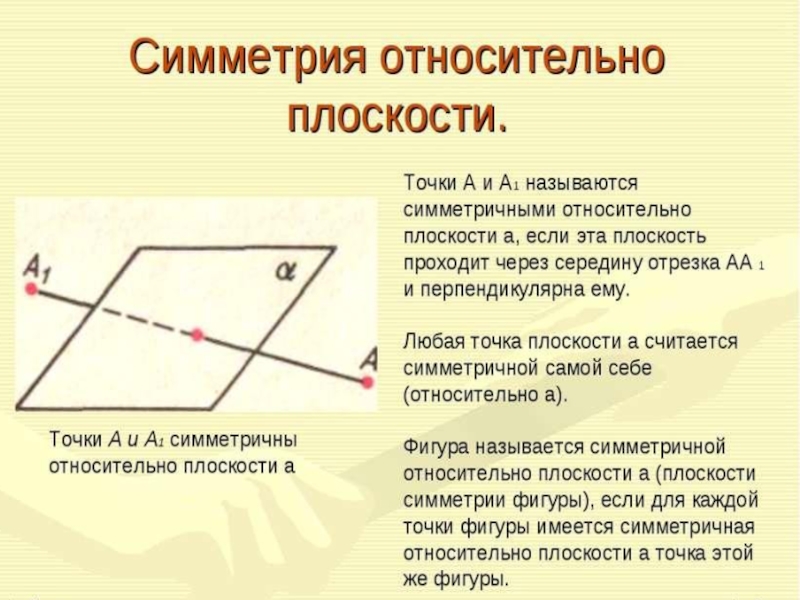
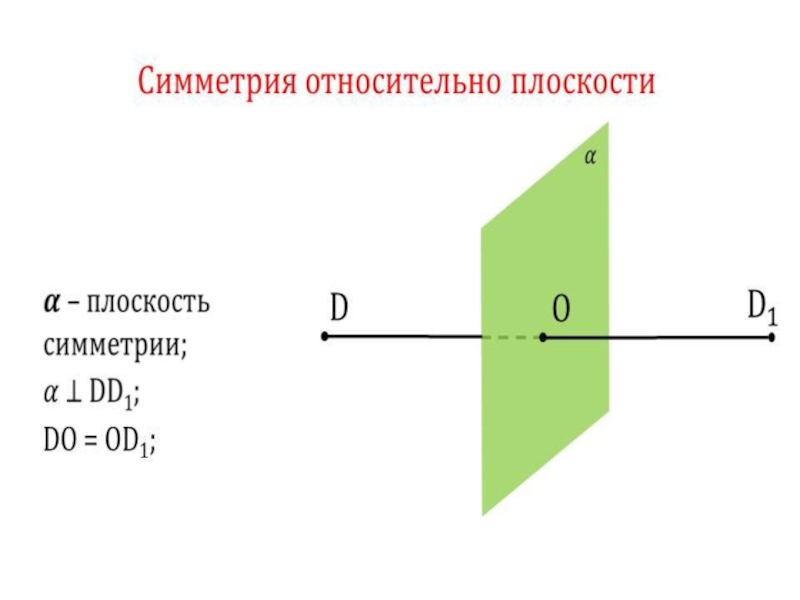
3)Симметрия относительно плоскости
4)Определение Центральной симметрии
5)Определение Осевой симметрии
6)Определение
Поворотной симметрии
7)Параллельный перенос
8)Определение Оси симметрии
9)Определение Центр симметрии
10)Зеркальная симметрия
11)Винтовая ось симметрии
12)Скользящая симметрия
Слайд 3Симметрия, в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях (например: положения, энергии, информации,
другого). Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.
Слайд 4ВИДЫ СИММЕТРИИ
✔Центральная симметрия
✔Осевая (зеркальная) симметрия
✔Поворотная симметрия
✔Параллельный перенос
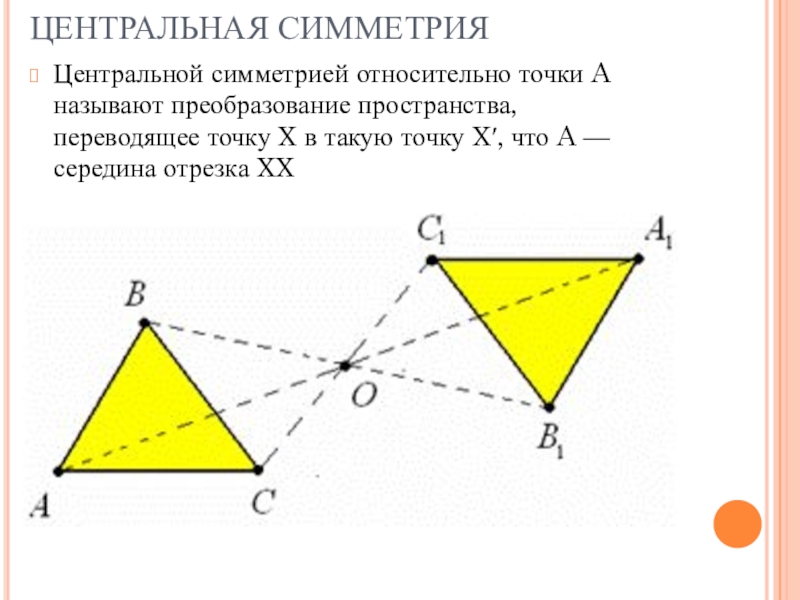
Слайд 7ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
Центральной симметрией относительно точки A называют преобразование пространства, переводящее точку X
в такую точку X′, что A — середина отрезка XX
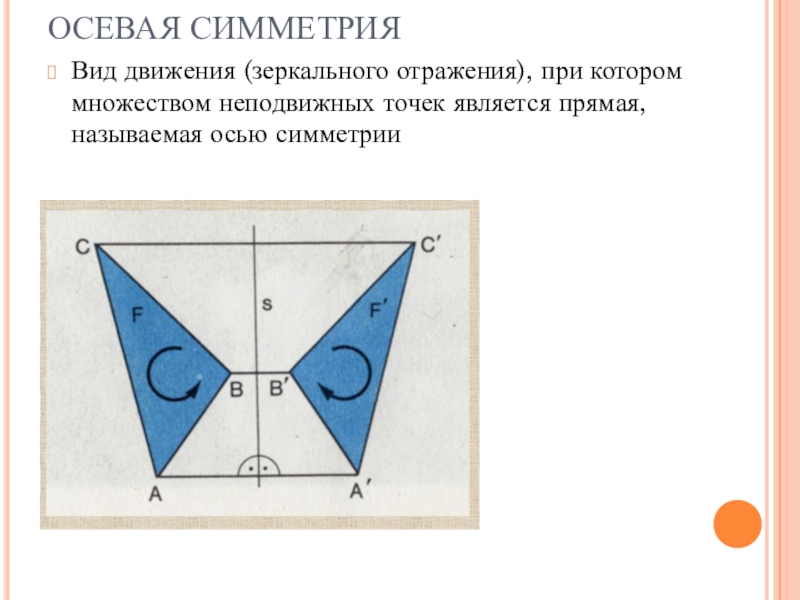
Слайд 8ОСЕВАЯ СИММЕТРИЯ
Вид движения (зеркального отражения), при котором множеством неподвижных точек
является прямая, называемая осью симметрии
Слайд 9ПОВОРОТНАЯ СИММЕТРИЯ
Поворотная симметрия – это такая симметрия при которой объект совмещает
сам с собой при повороте вокруг некоторой оси на угол равный 360
Слайд 10ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном
и том же направлении на одно и то же расстояние. Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении», которое само нуждается в точном определении.
Слайд 11ОСЬ СИММЕТРИИ
Ось симметрии – воображаемая ось, при повороте вокруг которой на некоторый
угол фигура совмещается сама с собой в пространстве. Она обозначается буквой L. У кристаллов при вращении вокруг оси симметрии на полный оборот одинаковые элементы ограничения (грани, ребра, углы) могут повторяться только 2, 3, 4, 6 раз. Соответственно этому оси будут называться осями симметрии второго, третьего, четвертого и шестого порядка и обозначаться: L2, L3, L4 и L6.Порядок оси определяется числом совмещений при повороте на 360⁰С.
Слайд 12ЦЕНТР СИММЕТРИИ
Центр симметрии – это точка внутри кристалла, в которой пересекаются и
делятся пополам линии, соединяющие одинаковые элементы ограничения кристалла (грани, ребра, углы). Обозначается она буквой С. Практически присутствие центра симметрии будет сказываться в том, что каждое ребро многогранника имеет параллельное себе ребро, каждая грань – такую же параллельную себе зеркально-обратную грань. Если же в многограннике присутствуют грани, не имеющие себе параллельных, то такой многогранник не обладает центром симметрии.
Слайд 13Зеркальная симметрия или отражение — движение пространства, множество неподвижных точек которого является гиперплоскостью (в случае
трехмерного пространства — просто плоскостью). Термин зеркальная симметрия употребляется также для описания соответствующего типа симметрии объекта, то есть, когда объект при операции отражения переходит в себя. Это математическое понятие в оптике описывает соотношение объектов и их (мнимых) изображений при отражении в плоском зеркале. Проявляется во многих законах природы (в кристаллографии, химии, физике, биологии и т. д., а также в искусстве и искусствоведении).
Слайд 14ВИНТОВАЯ СИММЕТРИЯ
ОСЬ СИММЕТРИИ ВИНТОВАЯ — элемент симметрии бесконечных фигур (правильных систем точек).
Действие винтовой оси состоит из поворота вокруг оси симметрии и параллельного ей поступания. В зависимости от направления вращения вокруг оси (по часовой стрелке или против часовой стрелки) они могут быть правыми и левыми. В кристаллических структурах могут быть лишь двойные, тройные, четверные и шестерные
Слайд 15
Скользящая симметрия — изометрия евклидовой плоскости.
Скользящей симметрией называют композицию симметрии относительно
некоторой прямой
и переноса на вектор, параллельный (этот вектор может
быть и нулевым).
Скользящую симметрию можно представить в виде композиции 3 осевых симметрий (теорема Шаля).
Скользящую симметрию можно представить в виде композиции 3 осевых симметрий (теорема Шаля).