- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Школьная лекция по теме Параллельность в пространстве 10 класс
Содержание
- 1. Школьная лекция по теме Параллельность в пространстве 10 класс
- 2. Основные определения: две прямые в пространстве
- 3. Теоремы-признаки Две прямые параллельны между собой,
- 4. Теорема –признак параллельности прямой и
- 5. Теорема-признак параллельности плоскостейЕсли две пересекающихся прямых
- 6. Теоремы (для построения) Через точку вне прямой
- 7. Изображение пространственных фигур.Свойство 1. Если прямая параллельна
- 8. Основное правило: параллельность и отношение
- 9. Из свойств параллельного проектирования следует, что параллельной
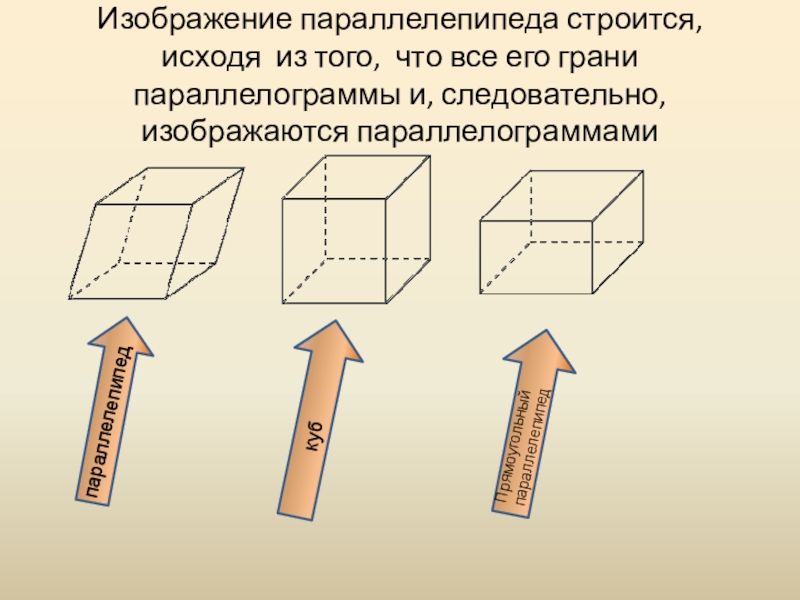
- 10. Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами
- 11. Для того чтобы построить изображение призмы, достаточно
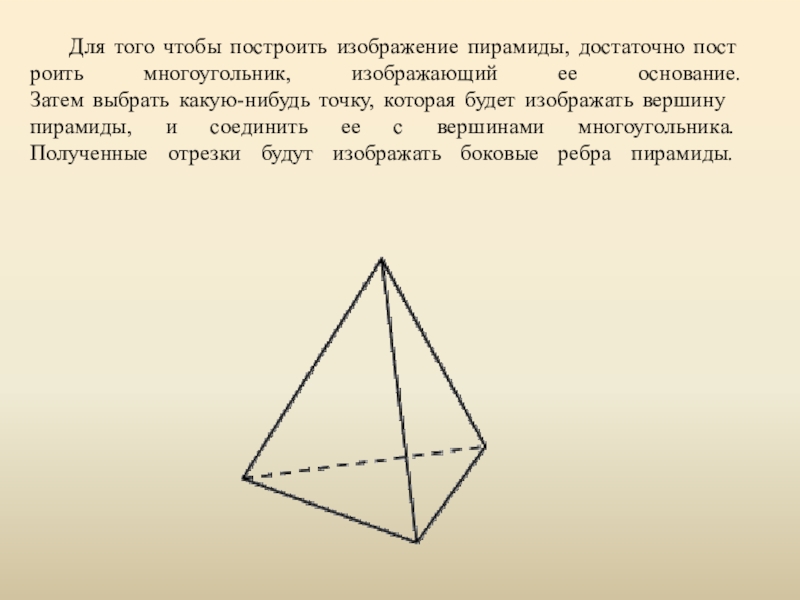
- 12. Для того чтобы построить изображение пирамиды, достаточно
- 13. Упражнения 1. В каком случае параллельной
- 14. 5. Верно ли, что если длина отрезка
- 15. Параллельными проекциями каких многогранников являются фигуры, изображенные
- 16. Верно ли? Для любых двух прямых
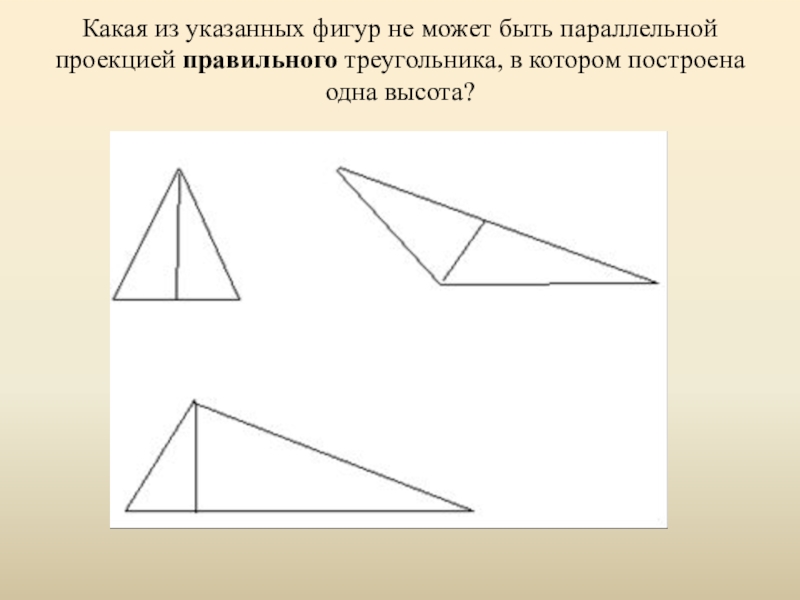
- 17. Какая из указанных фигур не может быть
- 18. Какая из указанных фигур не может быть проекцией пространственного четырёхугольника?
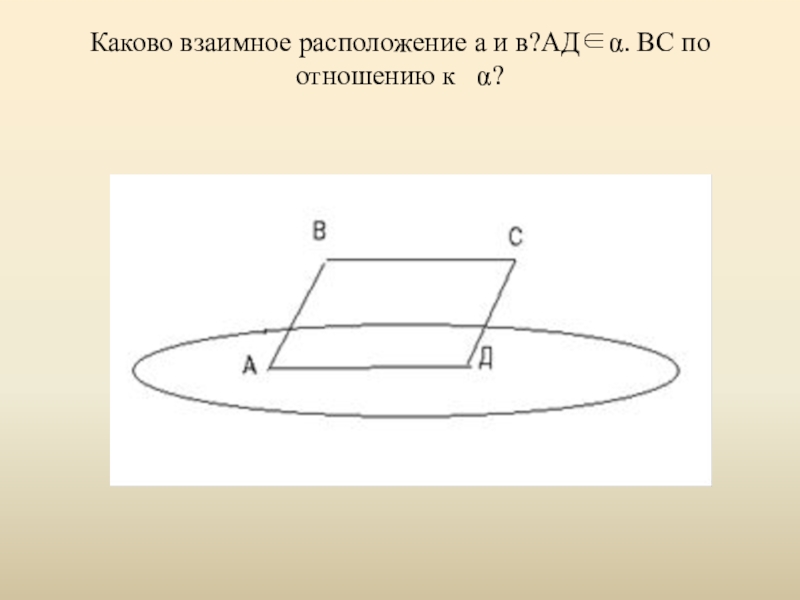
- 19. Каково взаимное расположение а и в?АДα. ВС по отношению к α?
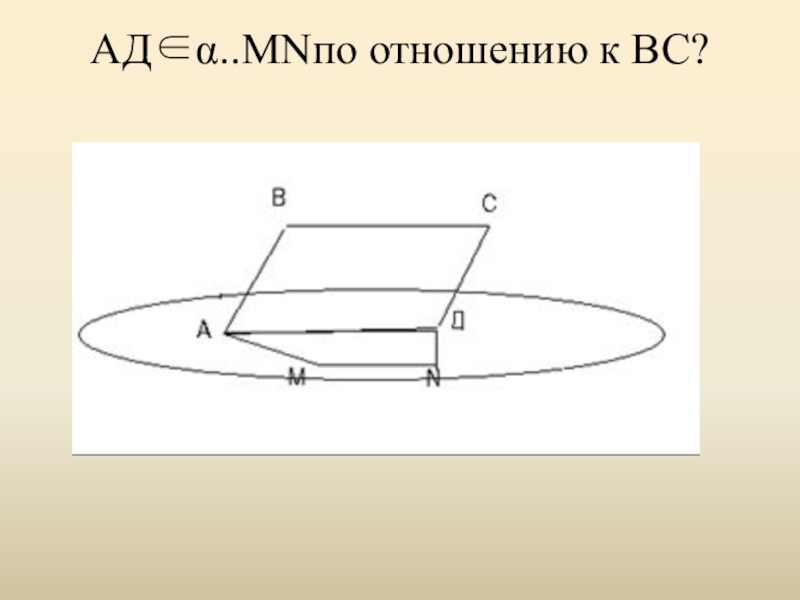
- 20. АДα..МNпо отношению к ВС?
- 21. В пространстве даны прямая и точка А.
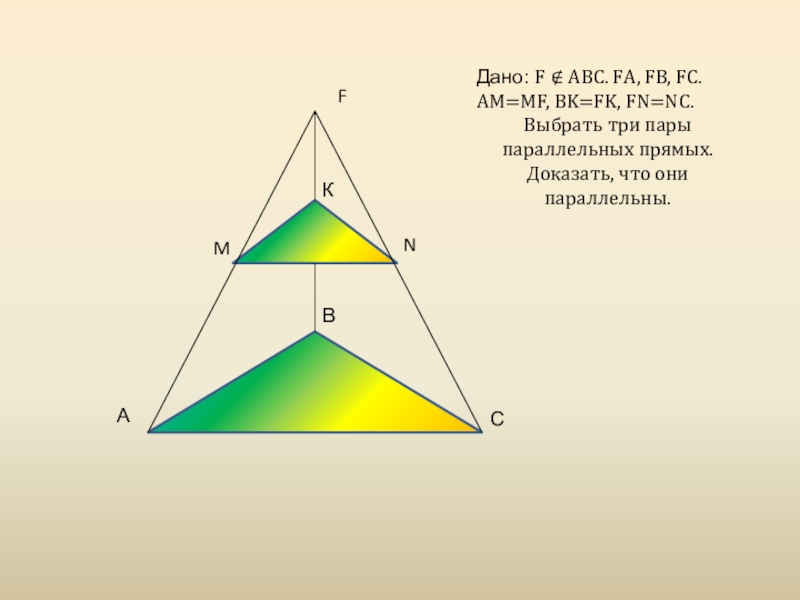
- 22. САВFNMКДано: F ∉ АВС. FА, FВ, FС.
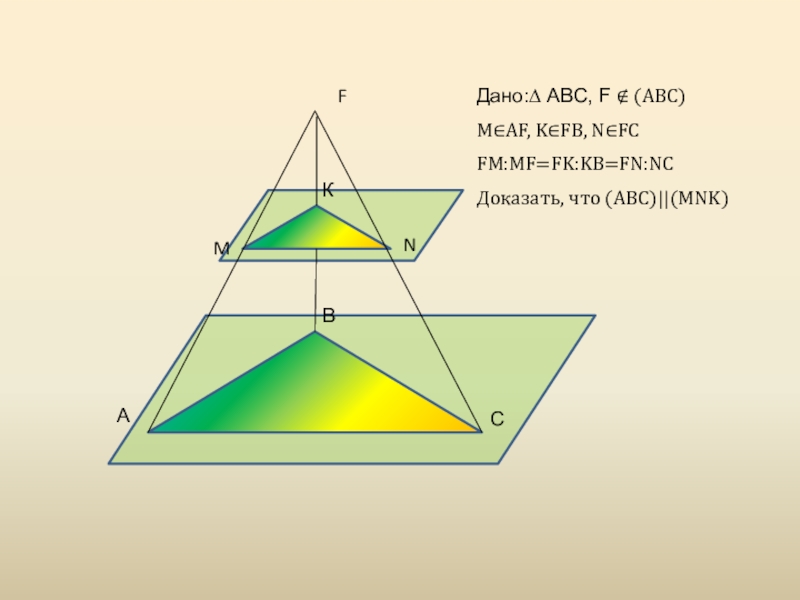
- 23. САВFNMКДано:∆ АВС, F ∉ (АВС)M∈AF, K∈FB, N∈FCFM:MF=FK:KB=FN:NCДоказать, что (ABC)||(MNK)
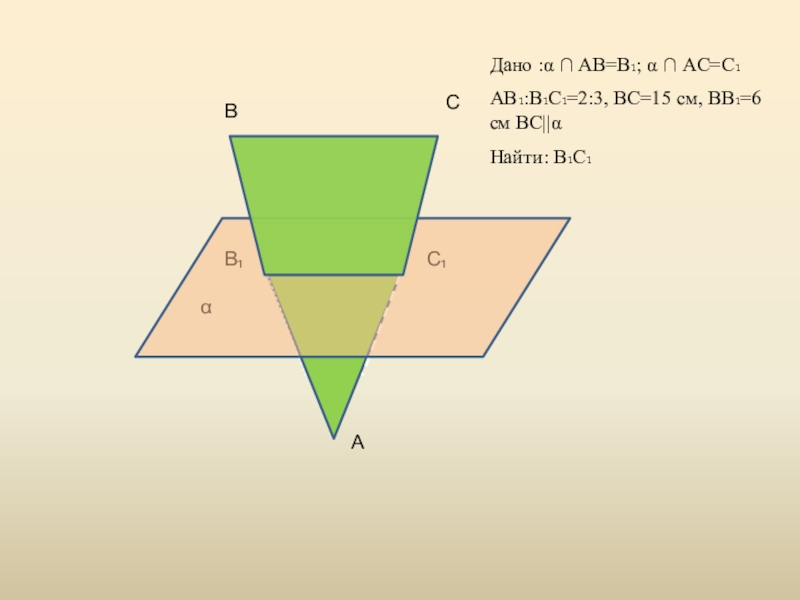
- 24. ВСС₁В₁АαДано :α ∩ AB=B₁; α ∩ AC=C₁AB₁:B₁C₁=2:3, BC=15 см, ВВ₁=6 см BC||αНайти: В₁С₁
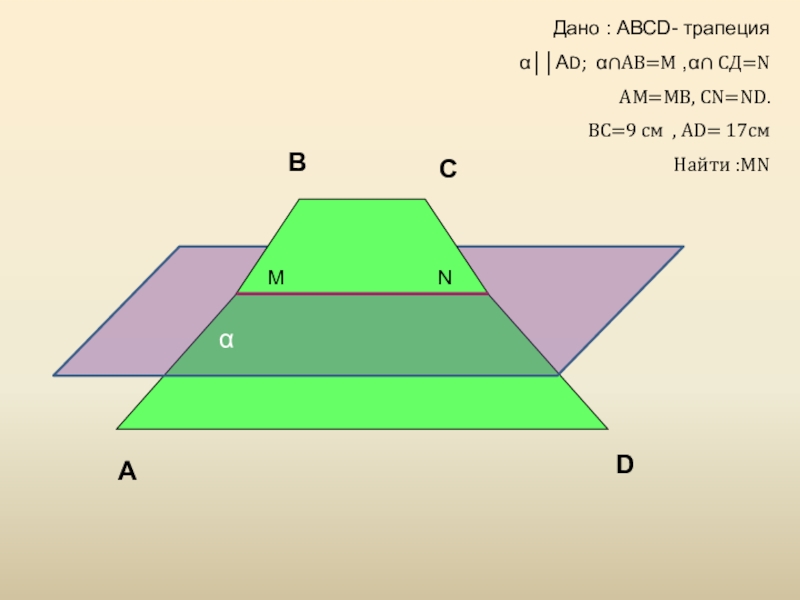
- 25. αMNABCDДано : АВСD- трапецияα││АD; α∩АВ=М ,α∩ СД=NAM=MB, CN=ND.BC=9 см , AD= 17смНайти :MN
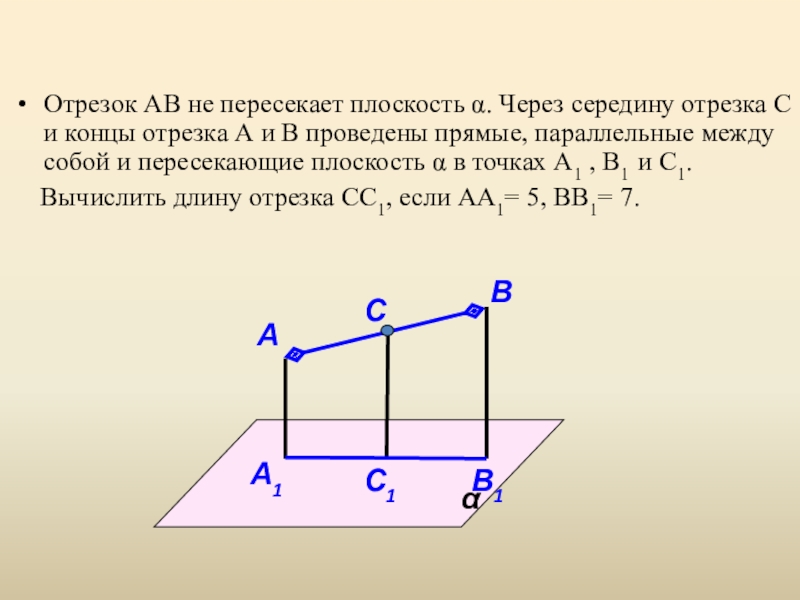
- 26. Отрезок АВ не пересекает плоскость α. Через
Слайд 2Основные определения:
две прямые в пространстве параллельны, если они лежат в
две плоскости называются параллельными, если они не пересекаются.
плоскость и прямая называются параллельными, если они не пересекаются.
Слайд 3Теоремы-признаки
Две прямые параллельны между собой, если они каждая параллельны третьей
Если прямая, не принадлежащая плоскости параллельна какой-либо прямой в этой плоскости, то она параллельна самой плоскости.
Если две пересекающихся прямых одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны между собой.
Слайд 4
Теорема –признак
параллельности прямой и плоскости.
Если прямая, не лежащая в плоскости
Доказательство:
Пусть есть прямая а в плоскости α , а вне её есть прямая в, причём а//в. Докажем , что в//α.
Пусть не параллельна, тогда прямая в пересекает плоскость в некоторой точке С.
Так как через две пересекающиеся прямые проходит плоскость β, то плоскость α имеет с плоскостью β общую точку С, а значит пересекается по прямой а.
Тогда через точку С проходят две различные прямые, которые по предположению пересекаются, а по условию параллельны.
Этого быть не может, значит, предположение не верно, и прямая а//α.
Слайд 5Теорема-признак
параллельности плоскостей
Если две пересекающихся прямых одной плоскости соответственно параллельны двум
Пусть плоскости пересекаются. Тогда прямая с принадлежит и плоскости α и плоскости β.
Получается, что если сα, то с//а и с//в, лежащих в плоскости β , так как если прямая параллельна плоскости, тогда она параллельна любой прямой этой плоскости.
Значит, через точку С проходит две различные параллельные прямые. Что является противоречием, а значит плоскость α параллельна плоскости β.
Слайд 6Теоремы
(для построения)
Через точку вне прямой можно провести прямую параллельную данной и
Через точку вне плоскости можно провести плоскость параллельную данной и только одну.
Если две параллельные плоскости пересечены третьей, то прямые пересечения параллельны.
Отрезки параллельных прямых, заключённые между двумя параллельными прямыми равны между собой .
Слайд 7Изображение пространственных фигур.
Свойство 1. Если прямая параллельна или совпадает с прямой
Свойство 2. Проекция отрезка при параллельном проектировании есть точка или отрезок, в зависимости от того лежит он на прямой, параллельной или совпадающей с прямой l, или нет. Параллельное проектирование сохраняет отношение длин отрезков, лежащих на прямой, не параллельной и не совпадающей с прямой l. В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.
Свойство 3. Если две параллельные прямые не параллельны прямой l, то их проекции в направлении l могут быть или параллельными прямыми или одной прямой.
Свойство 4. Если плоская фигура F лежит в плоскости, параллельной плоскости проектирования π, то ее проекция F’ на эту плоскость будет равна фигуре F.
Пусть F - некоторая фигура в пространстве.
Проекции ее точек на плоскость α образуют фигуру F ', которая называется параллельной проекцией фигуры Ф на плоскость α в направлении прямой l.
Говорят также, что фигура F ' получена из фигуры F параллельным проектированием.
Слайд 8 Основное правило: параллельность и отношение длин сохраняется, длины отрезков и углы,
на основании этого правила скажите
квадрат изображается?
прямоугольник изображается?
параллелограмм изображается?
медиана изображается?
высота изображается?
Круг изображается овалом или эллипсом .
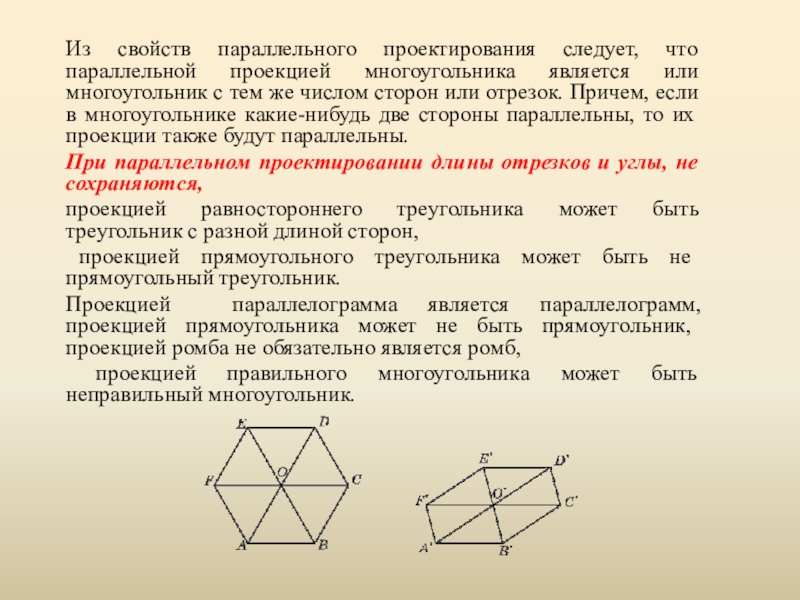
Слайд 9Из свойств параллельного проектирования следует, что параллельной проекцией многоугольника является или
При параллельном проектировании длины отрезков и углы, не сохраняются,
проекцией равностороннего треугольника может быть треугольник с разной длиной сторон,
проекцией прямоугольного треугольника может быть не прямоугольный треугольник.
Проекцией параллелограмма является параллелограмм, проекцией прямоугольника может не быть прямоугольник, проекцией ромба не обязательно является ромб,
проекцией правильного многоугольника может быть неправильный многоугольник.
Слайд 10Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы
Слайд 11Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий ее
Слайд 12Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий ее
Слайд 13
Упражнения
1. В каком случае параллельной проекцией прямой будет точка?
Ответ: Если прямая
2. В каком случае параллельной проекцией двух параллельных прямых является одна прямая?
Ответ: Если плоскость, в которой лежат эти прямые, параллельна направлению проектирования.
3. Какие фигуры могут быть параллельными проекциями двух скрещивающихся прямых?
Ответ: Две пересекающиеся прямые; две параллельные прямые; прямая и точка, ей не принадлежащая.
4. Сохраняются ли при параллельном проектировании: а) длины отрезков; б) величины углов?
Ответ: а), б) Нет.
Слайд 145. Верно ли, что если длина отрезка равна длине его параллельной
Ответ: Нет.
6. Может ли параллельной проекцией равностороннего треугольника быть: а) прямоугольный треугольник; б) равнобедренный треугольник; в) разносторонний треугольник?
Ответ: а), б), в) Да.
7. Может ли параллельной проекцией прямоугольника быть: а) квадрат; б) параллелограмм; в) ромб; г) трапеция?
Ответ: а), б), в) Да; г) нет.
8. Верно ли, что при параллельном проектировании треугольника: а) медианы проектируются в медианы; б) высоты проектируются в высоты; в) биссектрисы проектируются в биссектрисы?
Ответ: а) Да; б), в) нет.
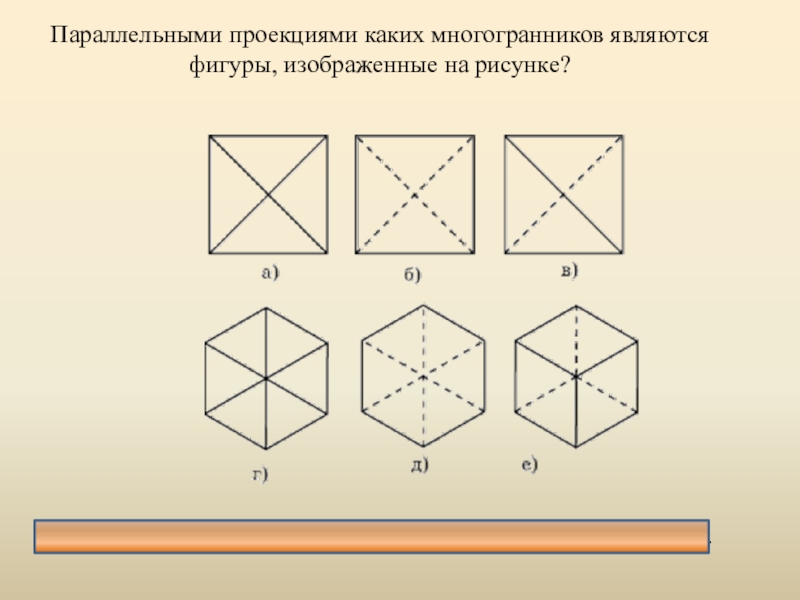
Слайд 15Параллельными проекциями каких многогранников являются фигуры, изображенные на рисунке?
Ответ: а), б)
Слайд 16
Верно ли?
Для любых двух прямых можно провести плоскость, параллельную каждой из
Все прямые , проходящие через данную точку, параллельно данной плоскости, лежат в одной плоскости.(да).
Сохраняется ли при параллельном проектировании отрезков одной плоскости их отношение?(да)
Может ли при параллельном проектировании трапеции получиться прямоугольник? (нет).
Может ли при параллельном проектировании параллелограмма получиться прямоугольник?(да)
Может ли параллельная проекция произвольного параллелограмма быть ромбом? (нет)
Если прямая параллельна плоскости, то она параллельна любой прямой, лежащей в плоскости? (нет)
Слайд 17Какая из указанных фигур не может быть параллельной проекцией правильного треугольника,
Слайд 21В пространстве даны прямая и точка А. Сколько существует прямых, которые
Через стороны АВ и СД четырёхугольника АВСД и точку К вне его проведены две плоскости , пересекающиеся по прямой параллельной каждой из прямых АВ иСД. Установите вид четырёхугольника АВСД, если известно, что АВ=СД.
Слайд 22С
А
В
F
N
M
К
Дано: F ∉ АВС. FА, FВ, FС.
АМ=MF, BK=FK, FN=NC.
Выбрать три
Слайд 26Отрезок АВ не пересекает плоскость α. Через середину отрезка С и
Вычислить длину отрезка СС1, если АА1= 5, ВВ1= 7.
α
А
В
С
А1
В1
С1