Галилео Галилей.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Сечения материал по геометрии для 10-11 класса
Содержание
- 1. Сечения материал по геометрии для 10-11 класса
- 2. СодержаниеОсновные понятияДемонстрация сеченийМетод следовМетод вспомогательных сеченийКомбинированный методТестЗащита проектов
- 3. Многогранником называюттело, поверхность которого состоит из конечного числа плоских многоугольников.Элементы многогранника: вершины, ребра, грани.
- 4. Сечением поверхности геометрических тел называется плоская фигура, полученная
- 5. сечение
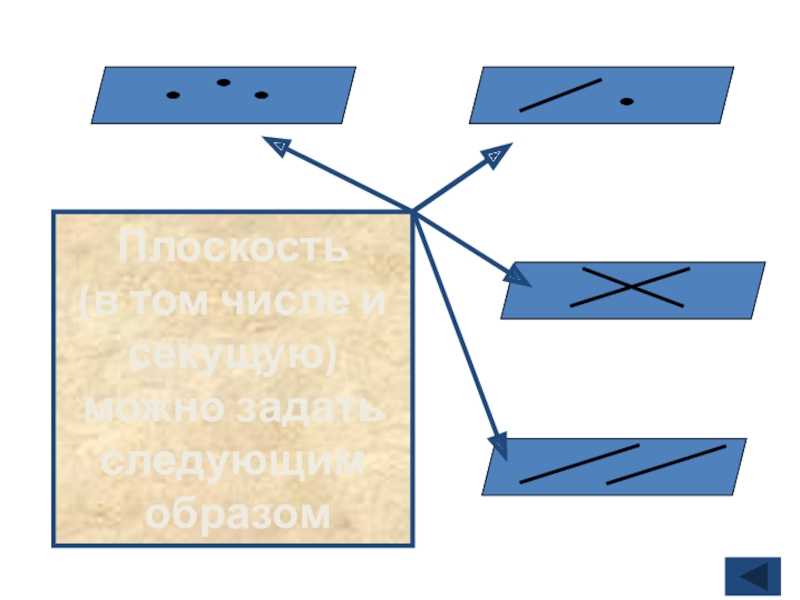
- 6. Плоскость (в том числе и секущую) можно задать следующим образом
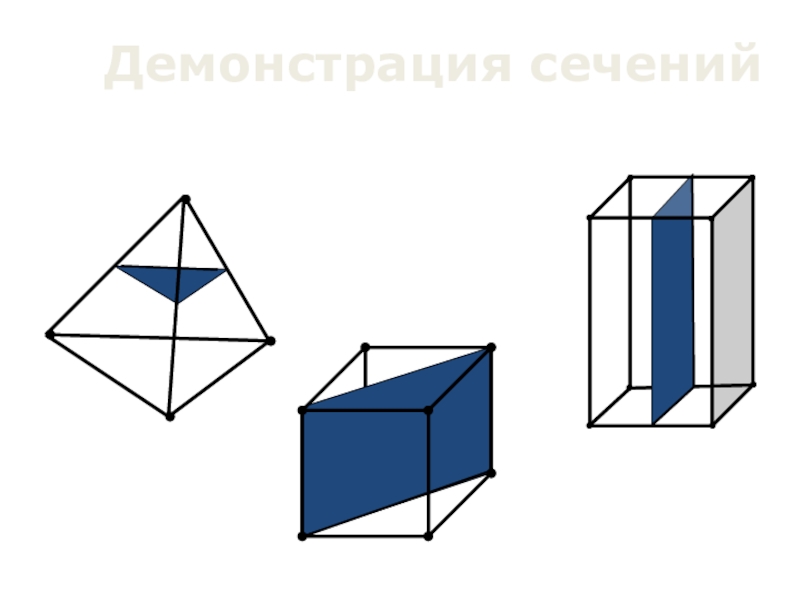
- 7. Демонстрация сечений
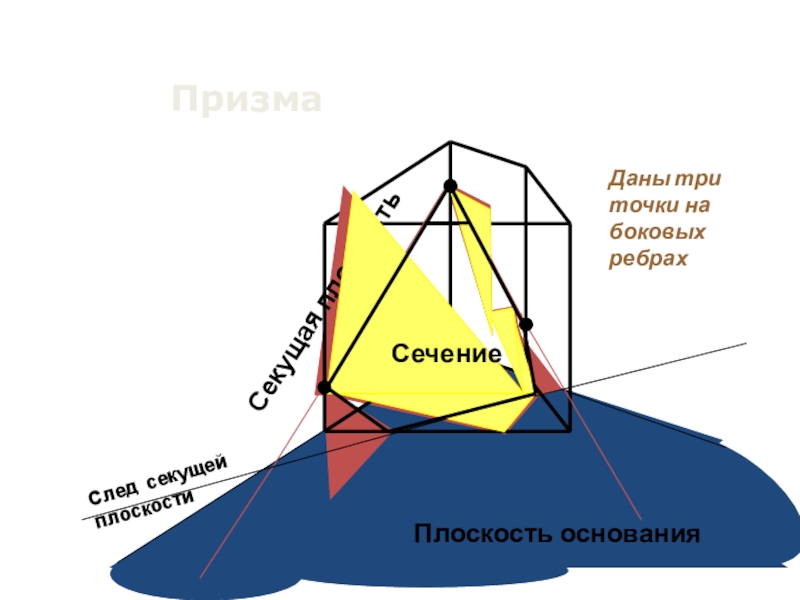
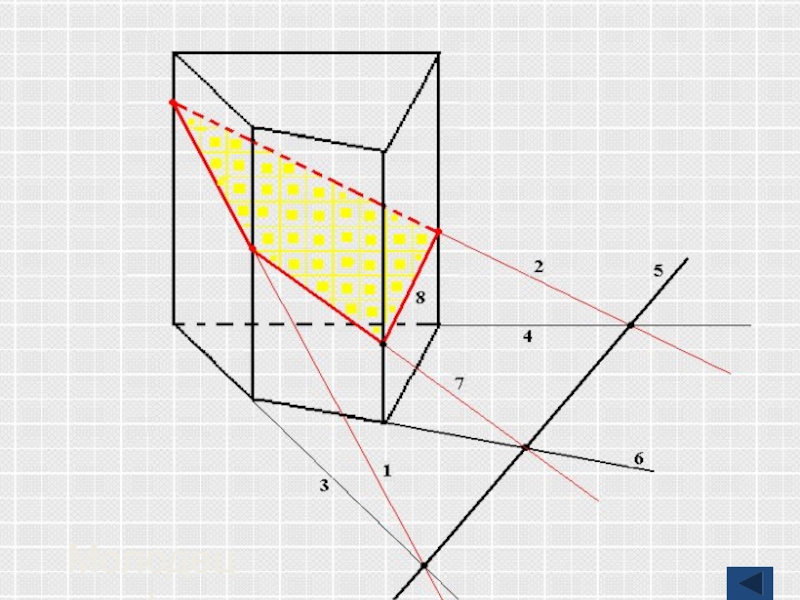
- 8. ПризмаПлоскость основанияСекущая плоскостьДаны три точки на боковых ребрахСечение
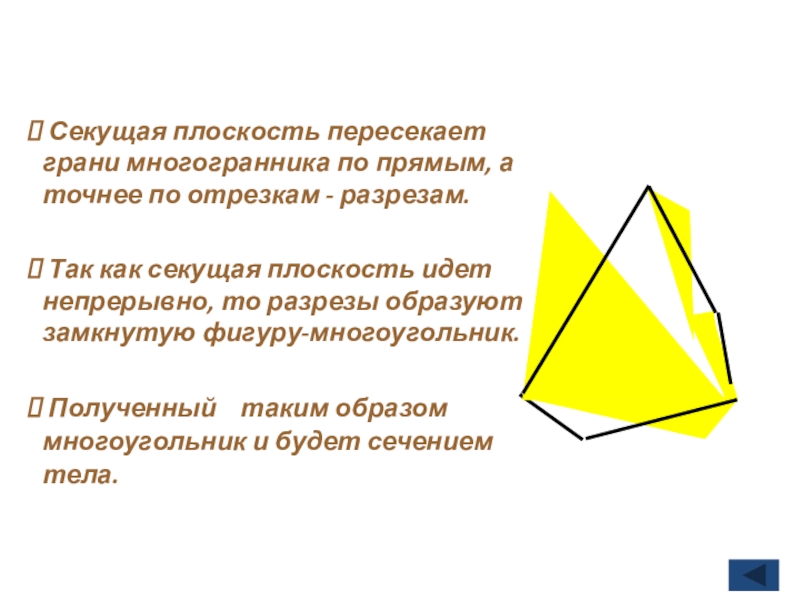
- 9. Секущая плоскость пересекает грани многогранника по
- 10. Методы построения сеченийАксиоматический метод Аксиомы стереометрии
- 11. Аксиоматический метод
- 12. ABCDKLMNFG Проводим через точки F и O
- 13. ABCDKLMNFG Шаг 2: ищем след секущей плоскости
- 14. ABCDKLMNFGШаг 3: делаем разрезы на других
- 15. CBADKLMNFGШаг 4: выделяем сечение многогранника Все разрезы
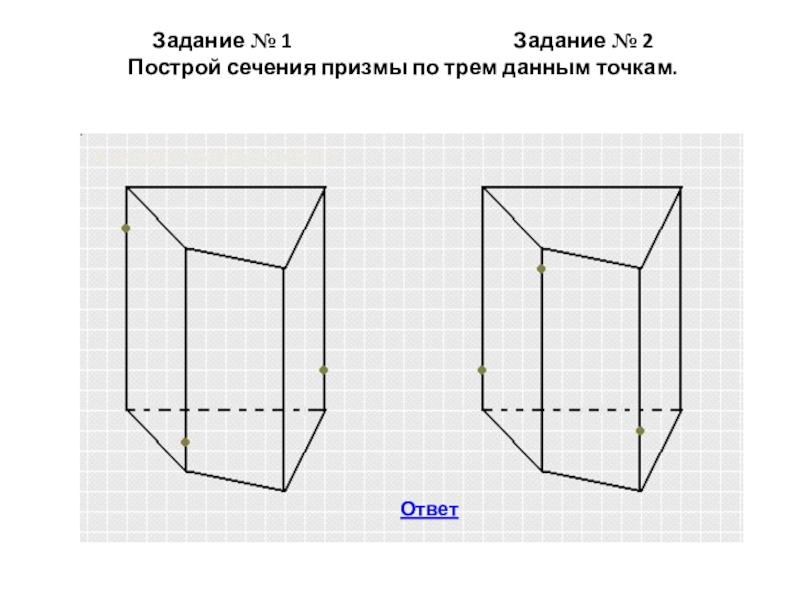
- 16. Задание № 1
- 17. Метод вспомогательных сечений Этот метод
- 18. На ребре BM пирамиды MABCD зададим точку
- 19. 3. Находим точку F, в которой пересекаются
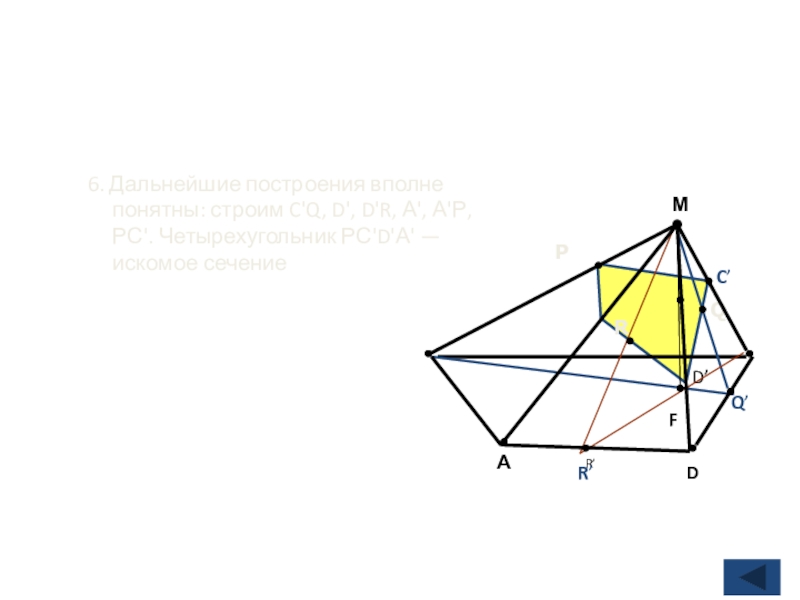
- 20. 6. Дальнейшие построения вполне понятны: строим C'Q,
- 21. Задание № 3
- 22. Комбинированный метод Суть комбинированного метода
- 23. Постройте сечение куба, проходящее через точки P,
- 24. ABCDA’B’C’D’RPQ4. Найдём точку пересечения прямых PR и
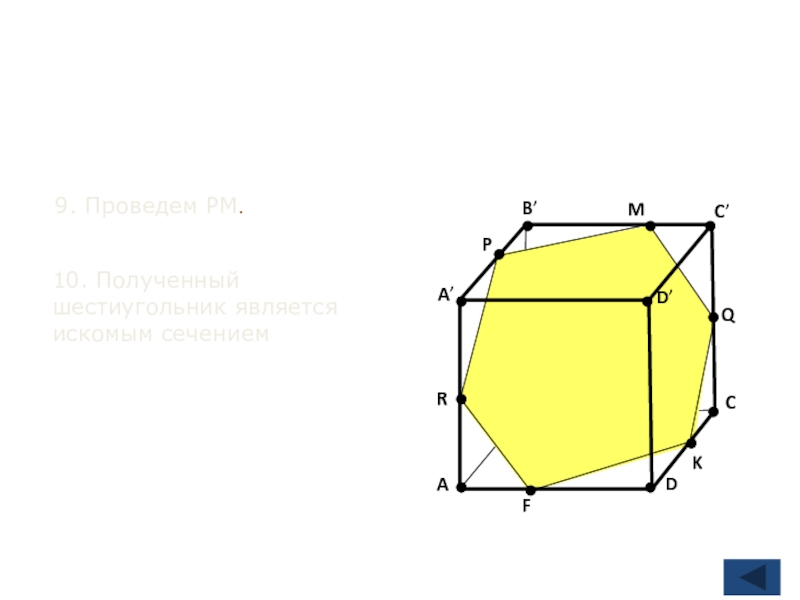
- 25. BACDA’B’C’D’RPQKFM9. Проведем PM.10. Полученный шестиугольник является искомым сечением
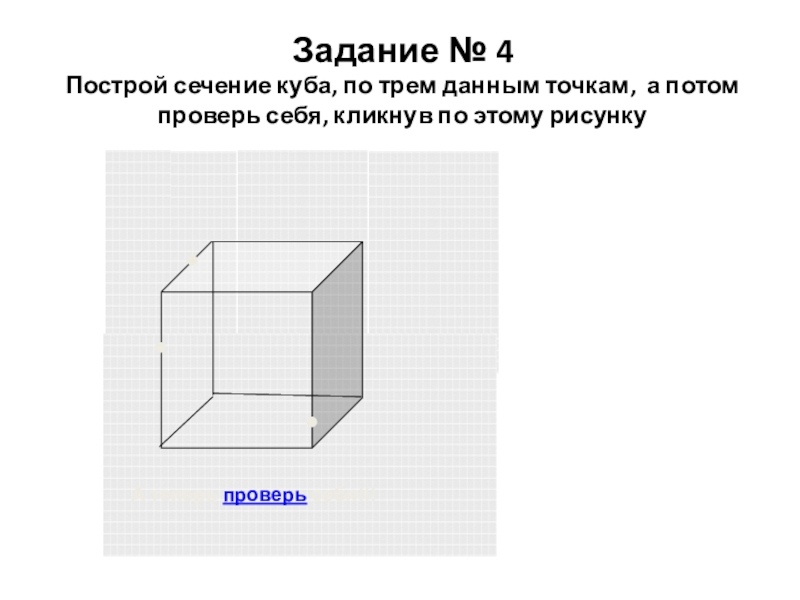
- 26. Задание № 4 Построй сечение куба, по
- 27. Защита проектов
- 28. ТЕСТДавайте, протестируемсяЖелаю удачи!
- 29. Отлично!
- 30. Молодец!
- 31. Молодцы! Я за вас рада. Если все сечения совпали, то тема усвоена!
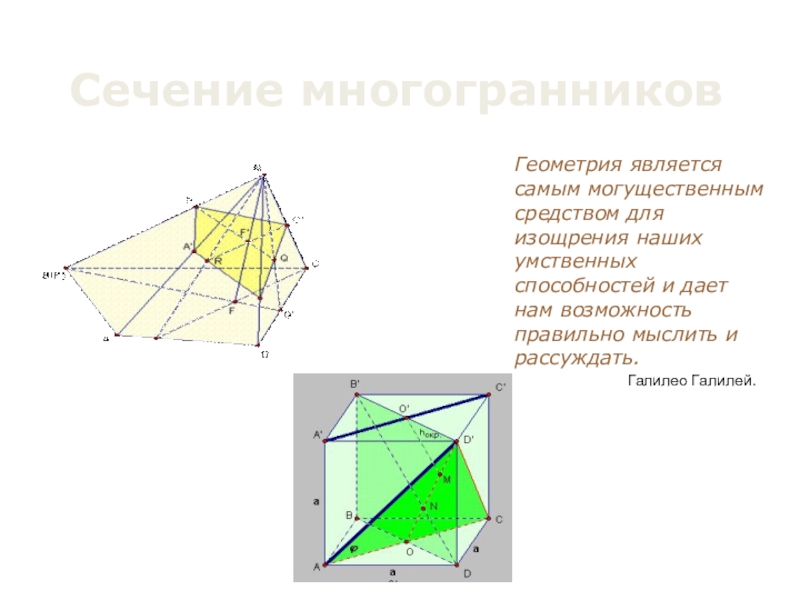
Слайд 1Сечение многогранников
Геометрия является самым могущественным средством для изощрения наших умственных способностей
Слайд 2Содержание
Основные понятия
Демонстрация сечений
Метод следов
Метод вспомогательных сечений
Комбинированный метод
Тест
Защита проектов
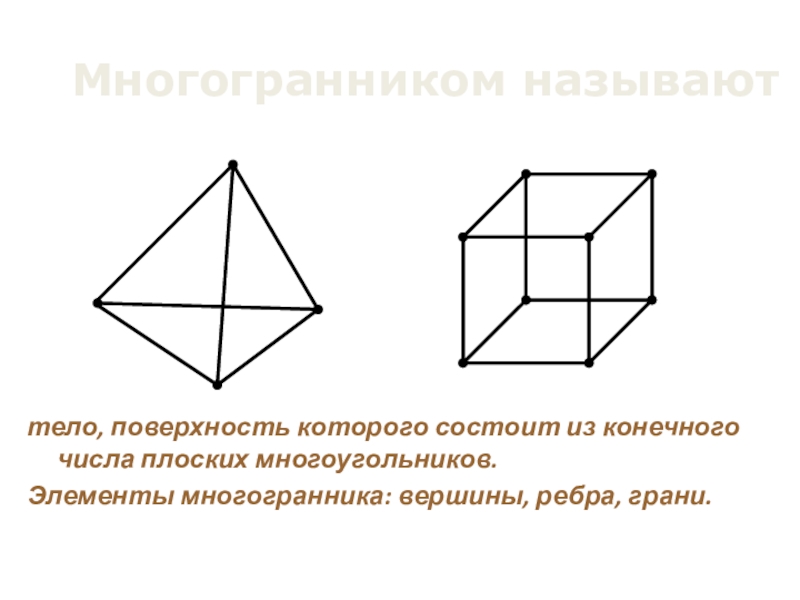
Слайд 3Многогранником называют
тело, поверхность которого состоит из конечного числа плоских многоугольников.
Элементы многогранника:
Слайд 4
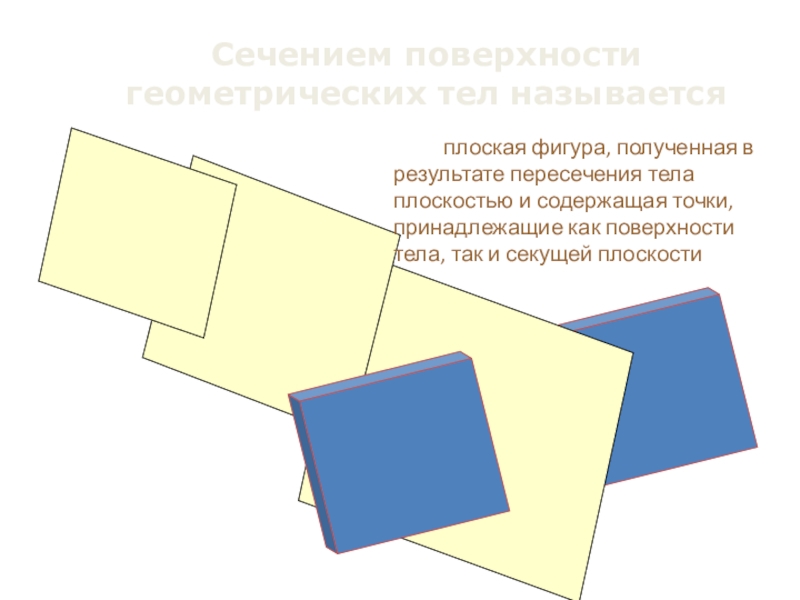
Сечением поверхности
геометрических тел называется
плоская фигура, полученная в результате пересечения тела плоскостью
Слайд 9 Секущая плоскость пересекает грани многогранника по прямым, а точнее по
Так как секущая плоскость идет непрерывно, то разрезы образуют замкнутую фигуру-многоугольник.
Полученный таким образом многоугольник и будет сечением тела.
Слайд 11 Аксиоматический метод
Метод следов
Суть метода заключается в построении
Слайд 12
A
B
C
D
K
L
M
N
F
G
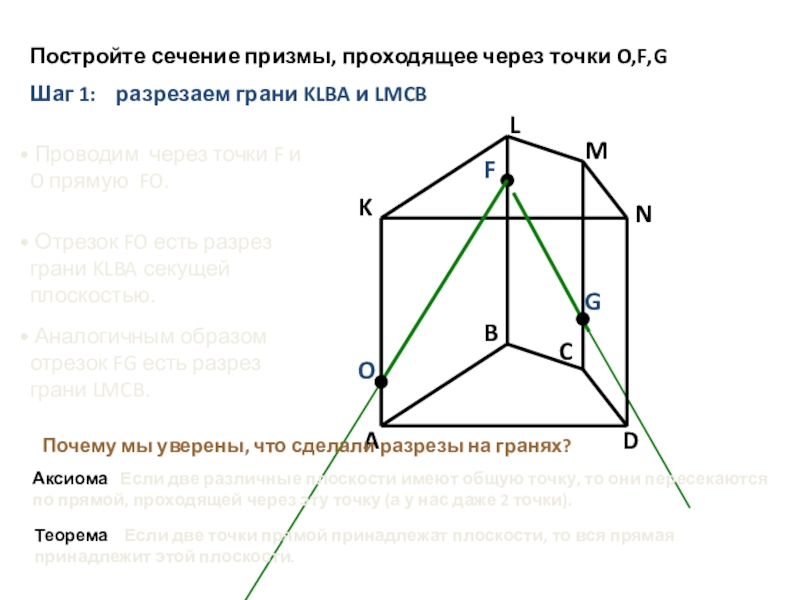
Проводим через точки F и O прямую FO.
O
Отрезок FO есть разрез грани KLBA секущей плоскостью.
Аналогичным образом отрезок FG есть разрез грани LMCB.
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Почему мы уверены, что сделали разрезы на гранях?
Постройте сечение призмы, проходящее через точки O,F,G
Шаг 1: разрезаем грани KLBA и LMCB
Слайд 13A
B
C
D
K
L
M
N
F
G
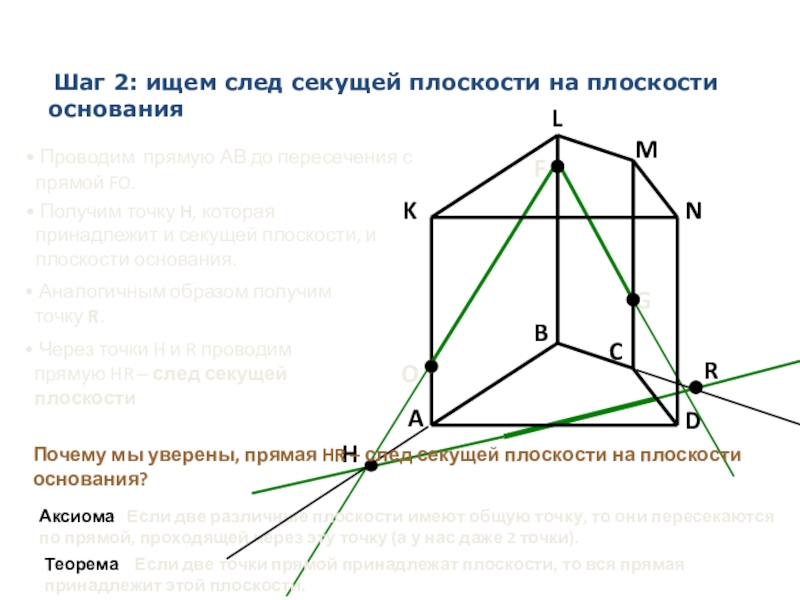
Шаг 2: ищем след секущей плоскости на плоскости основания
Проводим
O
Получим точку H, которая принадлежит и секущей плоскости, и плоскости основания.
Аналогичным образом получим точку R.
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Через точки H и R проводим прямую HR – след секущей плоскости
Почему мы уверены, прямая HR – след секущей плоскости на плоскости основания?
Слайд 14
A
B
C
D
K
L
M
N
F
G
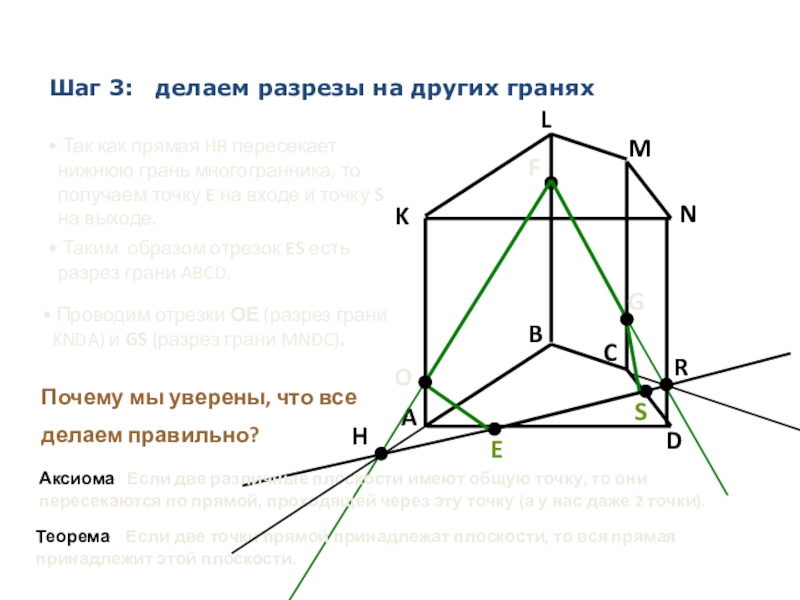
Шаг 3: делаем разрезы на других гранях
Так как прямая
O
Таким образом отрезок ES есть разрез грани ABCD.
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Проводим отрезки ОЕ (разрез грани KNDA) и GS (разрез грани MNDC).
Почему мы уверены, что все
делаем правильно?
Слайд 15C
B
A
D
K
L
M
N
F
G
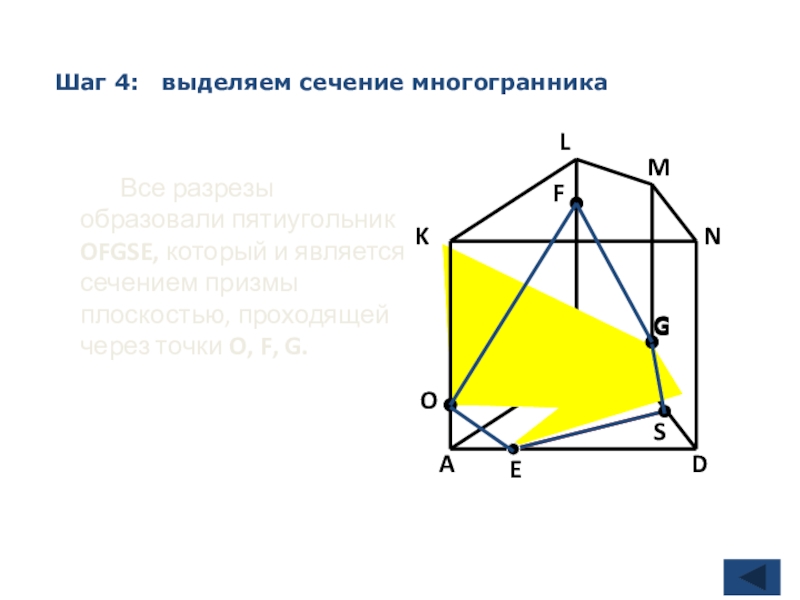
Шаг 4: выделяем сечение многогранника
Все разрезы образовали пятиугольник OFGSE, который
O
G
Слайд 16Задание № 1
Ответ
А теперь проверь себя!!!
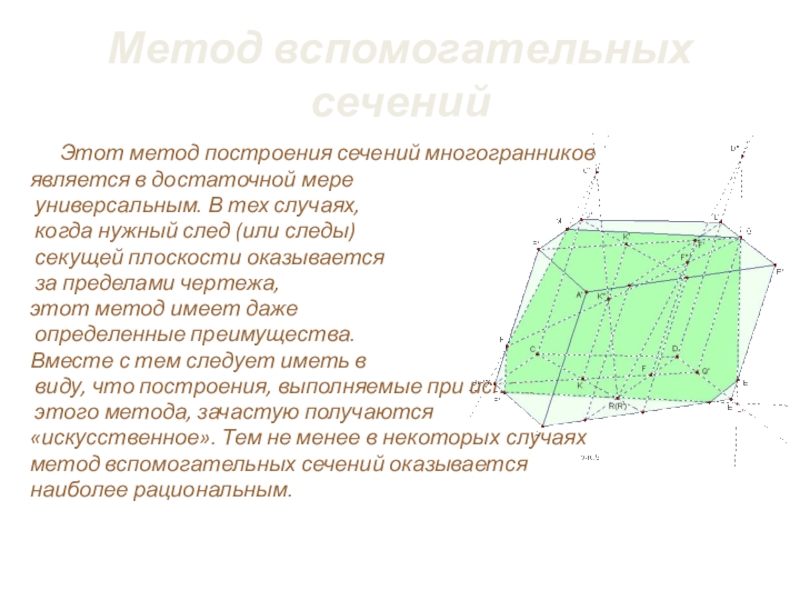
Слайд 17Метод вспомогательных сечений
Этот метод построения сечений многогранников
является
универсальным. В тех случаях,
когда нужный след (или следы)
секущей плоскости оказывается
за пределами чертежа,
этот метод имеет даже
определенные преимущества.
Вместе с тем следует иметь в
виду, что построения, выполняемые при использовании
этого метода, зачастую получаются
«искусственное». Тем не менее в некоторых случаях
метод вспомогательных сечений оказывается
наиболее рациональным.
Слайд 18
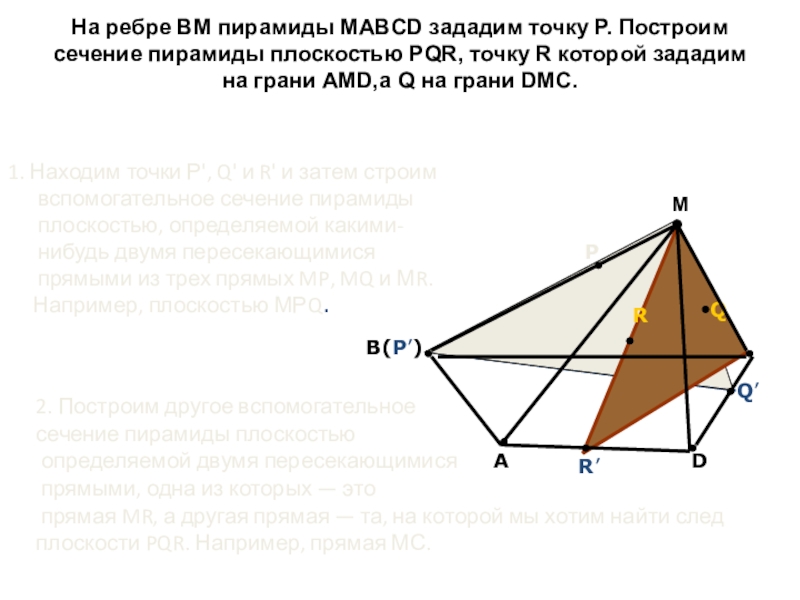
На ребре BM пирамиды MABCD зададим точку Р. Построим сечение пирамиды
1. Находим точки Р', Q' и R' и затем строим вспомогательное сечение пирамиды плоскостью, определяемой какими-нибудь двумя пересекающимися прямыми из трех прямых MP, MQ и МR.
Например, плоскостью МРQ.
B(P’)
2. Построим другое вспомогательное
сечение пирамиды плоскостью
определяемой двумя пересекающимися
прямыми, одна из которых — это
прямая MR, а другая прямая — та, на которой мы хотим найти след плоскости PQR. Например, прямая МС.
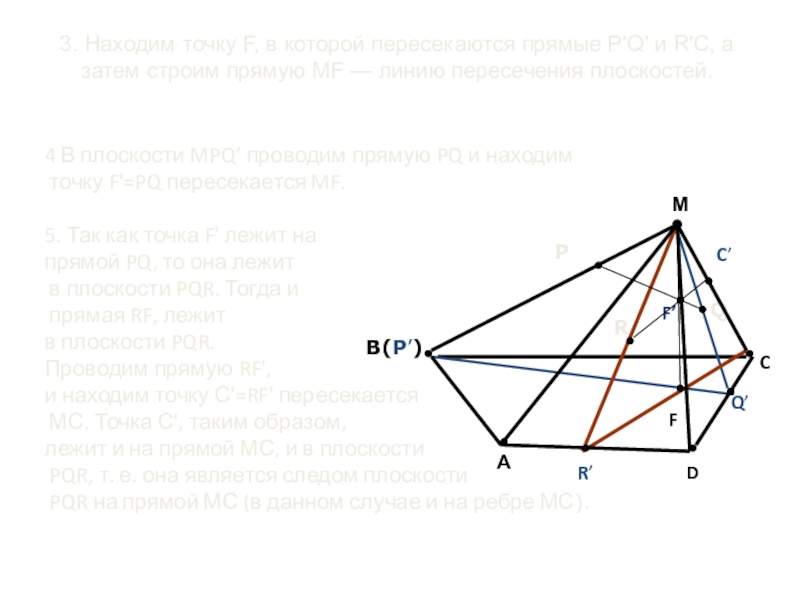
Слайд 193. Находим точку F, в которой пересекаются прямые Р'Q' и R'С,
4 В плоскости MPQ’ проводим прямую PQ и находим
точку F'=PQ пересекается MF.
5. Так как точка F' лежит на
прямой PQ, то она лежит
в плоскости PQR. Тогда и
прямая RF, лежит
в плоскости PQR.
Проводим прямую RF',
и находим точку С'=RF' пересекается
МС. Точка С', таким образом,
лежит и на прямой МС, и в плоскости
PQR, т. е. она является следом плоскости
PQR на прямой МС (в данном случае и на ребре МС).
B(P’)
P
R
Q
М
А
R’
D
C
Q’
F
F’
C’
Слайд 20
6. Дальнейшие построения вполне понятны: строим C'Q, D', D'R, А', А'Р,
D’
R’
P
R
Q
М
А
R’
D
Q’
F
C’
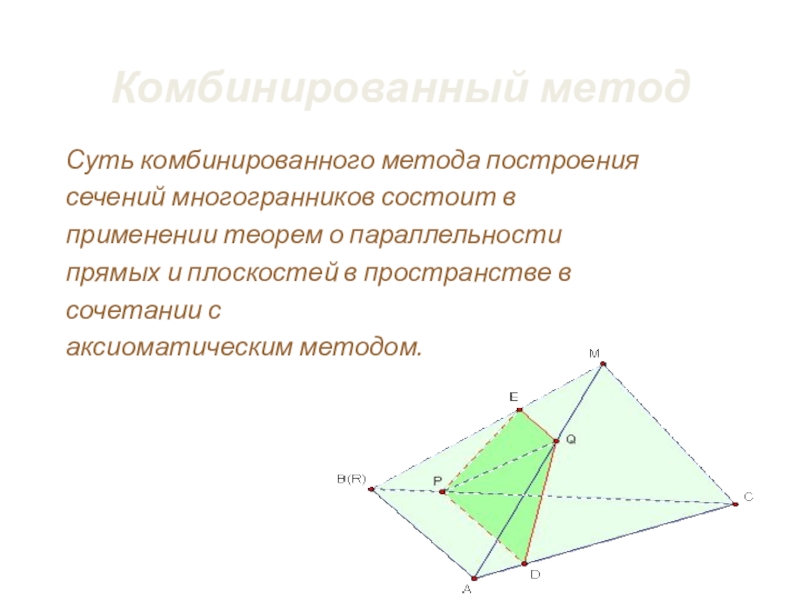
Слайд 22Комбинированный метод
Суть комбинированного метода построения
сечений многогранников состоит
применении теорем о параллельности
прямых и плоскостей в пространстве в
сочетании с
аксиоматическим методом.
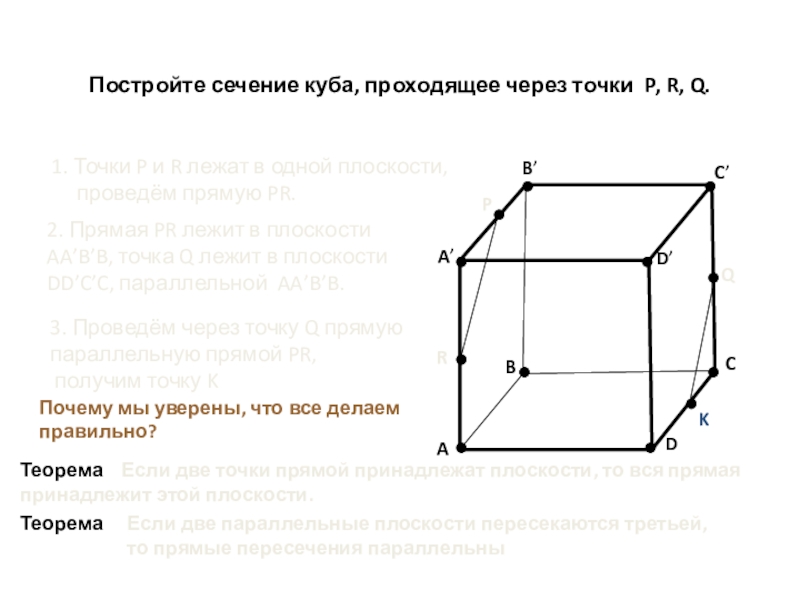
Слайд 23Постройте сечение куба, проходящее через точки P, R, Q.
A
B
C
D
A’
B’
C’
D’
R
P
Q
1. Точки
проведём прямую PR.
2. Прямая PR лежит в плоскости
AA’B’B, точка Q лежит в плоскости
DD’C’C, параллельной AA’B’B.
3. Проведём через точку Q прямую
параллельную прямой PR,
получим точку K
Почему мы уверены, что все делаем правильно?
Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Теорема
K
Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны
Слайд 24
A
B
C
D
A’
B’
C’
D’
R
P
Q
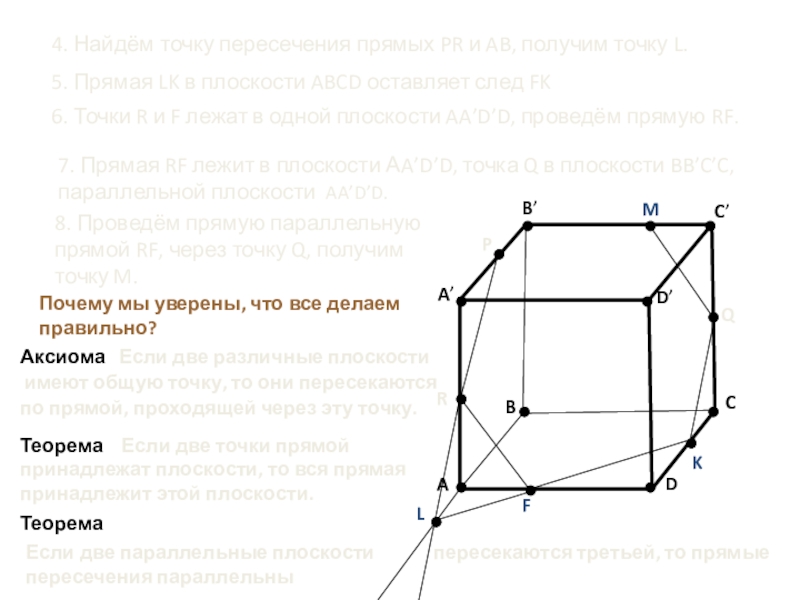
4. Найдём точку пересечения прямых PR и AB, получим точку L.
K
L
5.
F
6. Точки R и F лежат в одной плоскости AA’D’D, проведём прямую RF.
M
7. Прямая RF лежит в плоскости АA’D’D, точка Q в плоскости BB’C’C,параллельной плоскости AA’D’D.
8. Проведём прямую параллельную
прямой RF, через точку Q, получим
точку M.
Почему мы уверены, что все делаем правильно?
Аксиома Если две различные плоскости
имеют общую точку, то они пересекаются
по прямой, проходящей через эту точку.
Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Теорема
Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны
Слайд 26Задание № 4 Построй сечение куба, по трем данным точкам, а потом
А теперь проверь себя!!!