- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему РОМБ- МАТЕРИАЛЫ К УРОКУ.
Содержание
- 1. РОМБ- МАТЕРИАЛЫ К УРОКУ.
- 2. Слайд 2
- 3. Поскольку ромб – это параллелограмм, то он
- 4. Слайд 4
- 5. Диагонали ромба являются биссектрисами его углов. Доказательство:Пусть
- 6. Слайд 6
- 7. Если диагональ параллелограмма является биссектрисой его угла,
- 8. Найти углы, если диагональ его образует
- 9. Решение: АДО=180о-90о-20о – т.к. диагонали ромба пересекаются
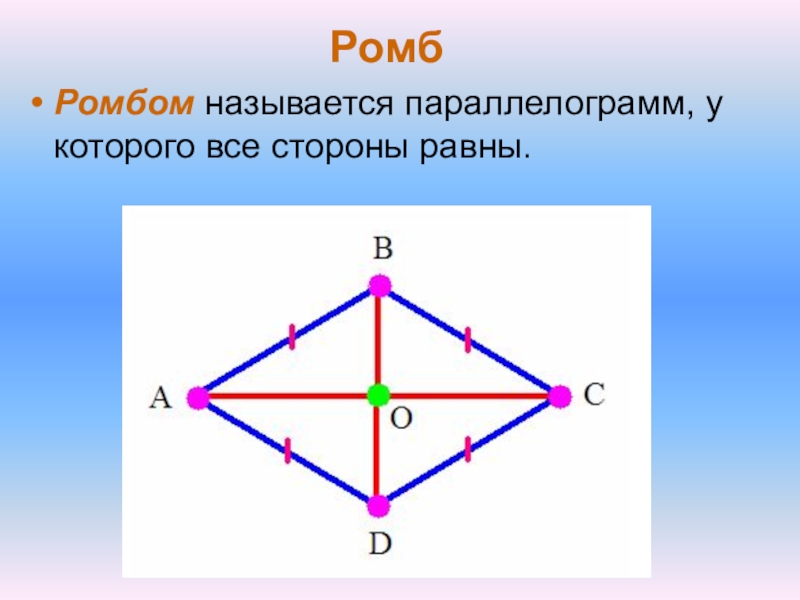
Ромб Ромбом называется параллелограмм, у которого все стороны равны.
Слайд 3
Поскольку ромб – это параллелограмм, то он обладает всеми свойствами параллелограмма.
Но ромб – это не просто параллелограмм, а параллелограмм, у которого все стороны равны. Поэтому у него есть еще два свойства, которые есть только у нее.
Слайд 4 Свойства
ромба.
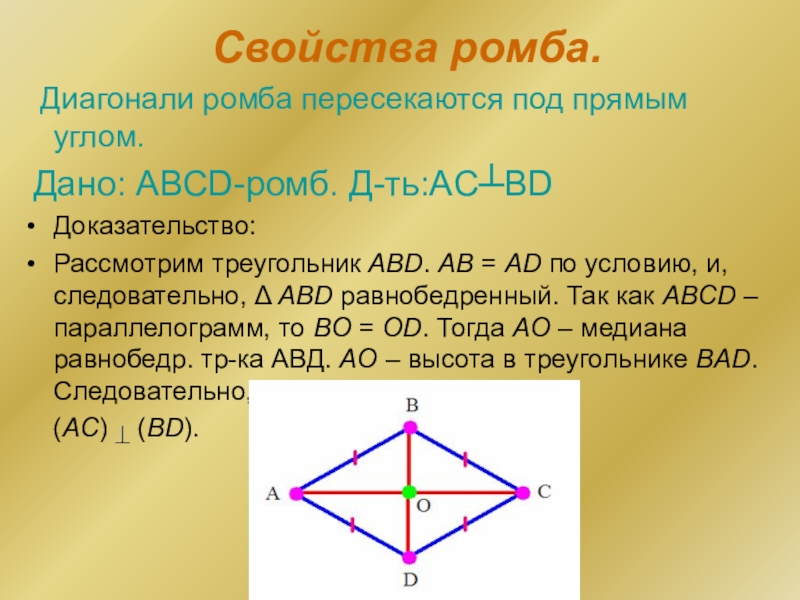
Диагонали ромба пересекаются под прямым углом.
Дано: АВСD-ромб. Д-ть:AC┴BD
Доказательство:
Рассмотрим треугольник ABD. AB = AD по условию, и, следовательно, Δ ABD равнобедренный. Так как ABCD – параллелограмм, то BO = OD. Тогда AO – медиана равнобедр. тр-ка АВД. AO – высота в треугольнике BAD. Следовательно,
(AC) (BD).
Диагонали ромба пересекаются под прямым углом.
Дано: АВСD-ромб. Д-ть:AC┴BD
Доказательство:
Рассмотрим треугольник ABD. AB = AD по условию, и, следовательно, Δ ABD равнобедренный. Так как ABCD – параллелограмм, то BO = OD. Тогда AO – медиана равнобедр. тр-ка АВД. AO – высота в треугольнике BAD. Следовательно,
(AC) (BD).
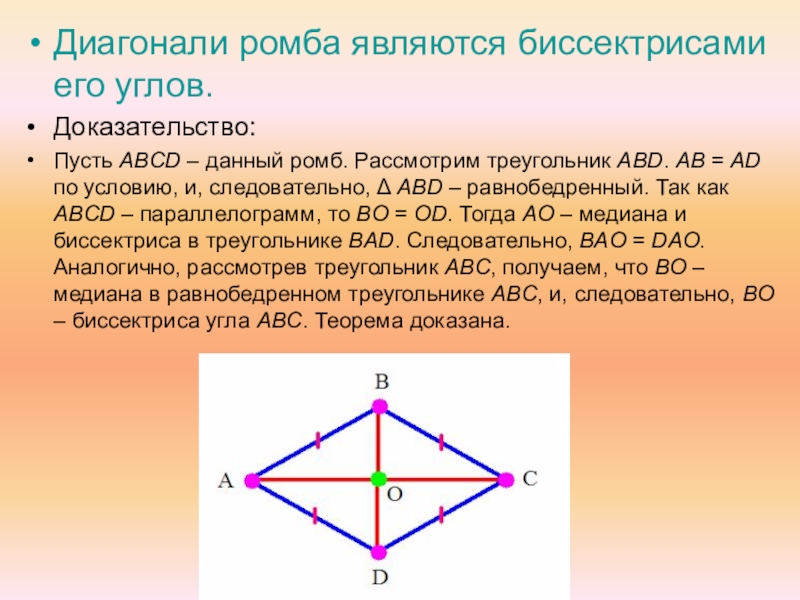
Слайд 5Диагонали ромба являются биссектрисами его углов.
Доказательство:
Пусть ABCD – данный ромб.
Рассмотрим треугольник ABD. AB = AD по условию, и, следовательно, Δ ABD – равнобедренный. Так как ABCD – параллелограмм, то BO = OD. Тогда AO – медиана и биссектриса в треугольнике BAD. Следовательно, BAO = DAO. Аналогично, рассмотрев треугольник ABC, получаем, что BO – медиана в равнобедренном треугольнике ABC, и, следовательно, BO – биссектриса угла ABC. Теорема доказана.
Слайд 6
Признаки ромба.
Если диагонали параллелограмма перпендикулярны, то параллелограмм – ромб.
Доказательство:
Пусть ABCD – данный параллелограмм, AC и BD – его диагонали и (AC) (BD). Пусть O – точка пересечения диагоналей параллелограмма. Треугольник ABC – равнобедренный с основанием AC. Действительно, так как диагонали параллелограмма в точке пересечения делятся пополам, то AO = OC, и тогда BO – медиана треугольника ABC, проведенная к стороне AC. Но по условию (BO) (AC) и [BO] – высота треугольника ABC. Тогда ABC – равнобедренный треугольник с основанием AC. Отсюда – AB = BC. По свойству равенства противоположных сторон параллелограмма следует, что AB = BC = CD = AD. Таким образом, данный параллелограмм – ромб. Теорема доказана.
Если диагонали параллелограмма перпендикулярны, то параллелограмм – ромб.
Доказательство:
Пусть ABCD – данный параллелограмм, AC и BD – его диагонали и (AC) (BD). Пусть O – точка пересечения диагоналей параллелограмма. Треугольник ABC – равнобедренный с основанием AC. Действительно, так как диагонали параллелограмма в точке пересечения делятся пополам, то AO = OC, и тогда BO – медиана треугольника ABC, проведенная к стороне AC. Но по условию (BO) (AC) и [BO] – высота треугольника ABC. Тогда ABC – равнобедренный треугольник с основанием AC. Отсюда – AB = BC. По свойству равенства противоположных сторон параллелограмма следует, что AB = BC = CD = AD. Таким образом, данный параллелограмм – ромб. Теорема доказана.
Слайд 7Если диагональ параллелограмма является биссектрисой его угла, то параллелограмм – ромб.
Доказательство:
Пусть ABCD – данный параллелограмм, AC – его диагональ и, при этом, AC – биссектриса угла A параллелограмма. Так как AC – биссектриса угла A, то BAC = CAD. С другой стороны, углы CAD и BCA внутренние накрест лежащие при параллельных прямых BC и AD и секущей AC и по теореме 3.4 BCA = CAD. Отсюда BAC = BCA и по признаку равнобедренного треугольника ABC равнобедренный, и, следовательно, AB = BC. Так как ABCD – параллелограмм, то AB = CD, BC = AD. Тогда AB = BC = CD = AD. Таким образом, ABCD – ромб. Теорема доказана.
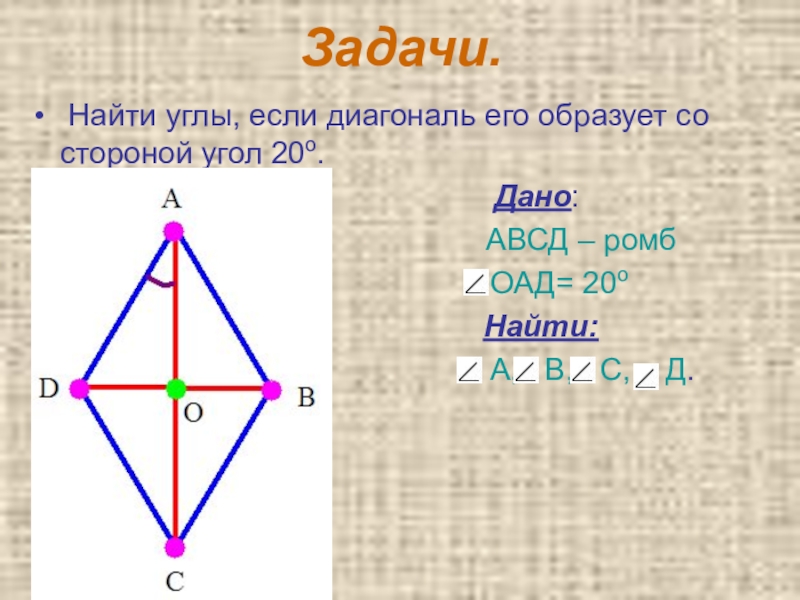
Слайд 8 Найти углы, если диагональ его образует со стороной угол 20о.
Дано:
АВСД – ромб
ОАД= 20о
Найти:
А, В, С, Д.
АВСД – ромб
ОАД= 20о
Найти:
А, В, С, Д.
Задачи.
Слайд 9Решение:
АДО=180о-90о-20о – т.к. диагонали ромба пересекаются под прямым углом. АДО=70о.
ВАО= 20о – т.к. у ромба диагональ является биссектрисой. Значит весь угол А равен 40о.
СДО=70о – аналогично. Следовательно, весь угол Д равен 140о.
С= А= 40о и В= Д=140о, потому что у ромба противоположные углы равны.
Ответ: 40о, 140о, 40о, 140о.
СДО=70о – аналогично. Следовательно, весь угол Д равен 140о.
С= А= 40о и В= Д=140о, потому что у ромба противоположные углы равны.
Ответ: 40о, 140о, 40о, 140о.