- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение задач по теме Площадь параллелограмма, треугольника, трапеции 8класс
Содержание
- 1. Решение задач по теме Площадь параллелограмма, треугольника, трапеции 8класс
- 2. Вычисление площадей фигур на клетчатой бумаге123456789101112
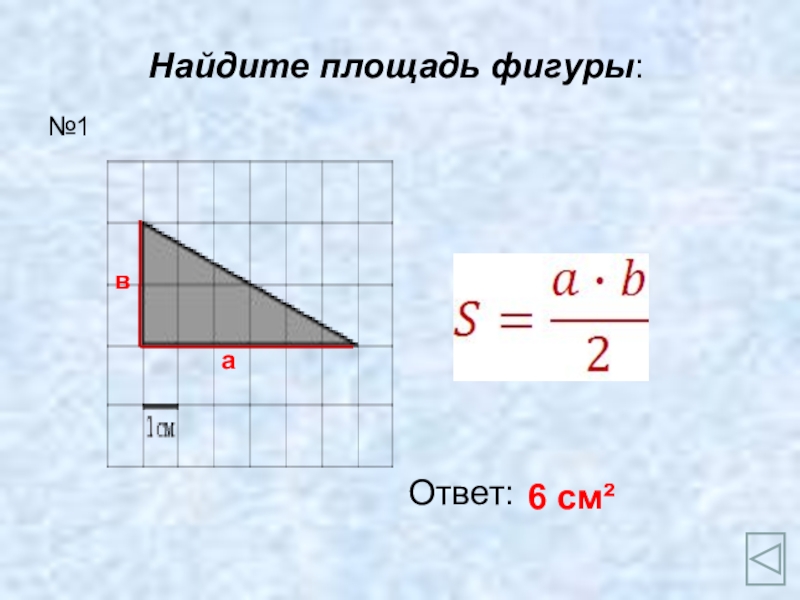
- 3. Найдите площадь фигуры:Ответ:6 см²№1
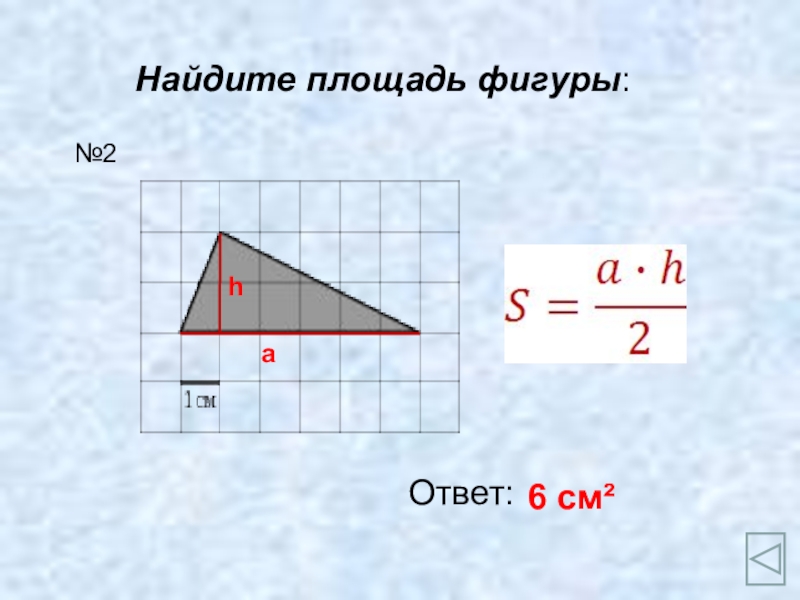
- 4. Найдите площадь фигуры:Ответ:6 см²№2
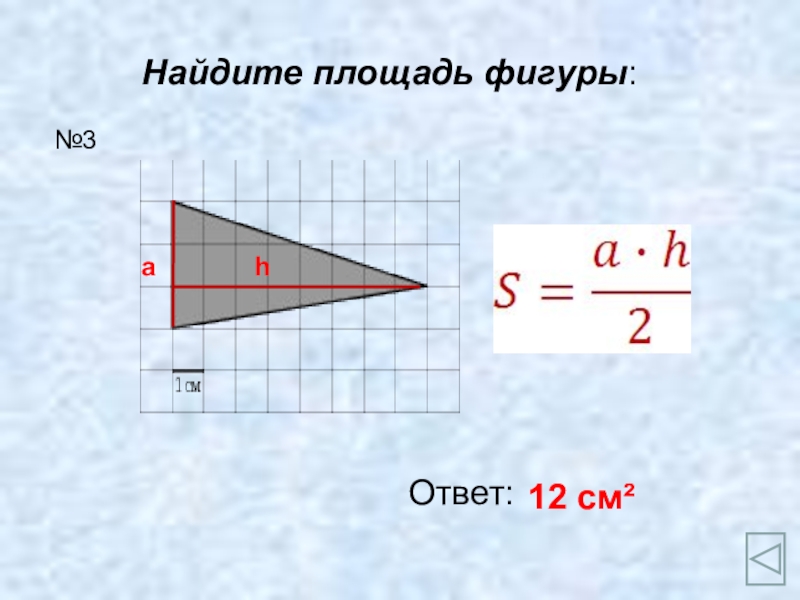
- 5. Найдите площадь фигуры:Ответ:12 см²№3
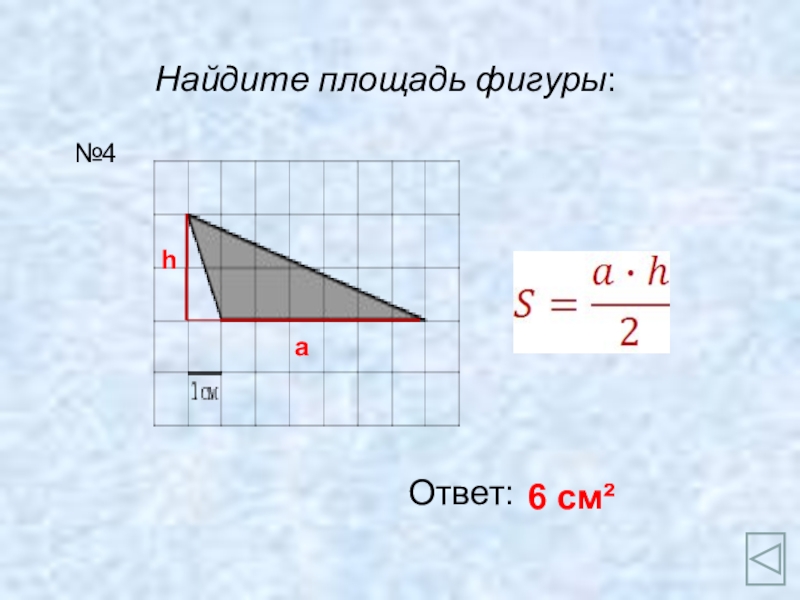
- 6. Найдите площадь фигуры:Ответ:6 см²№4
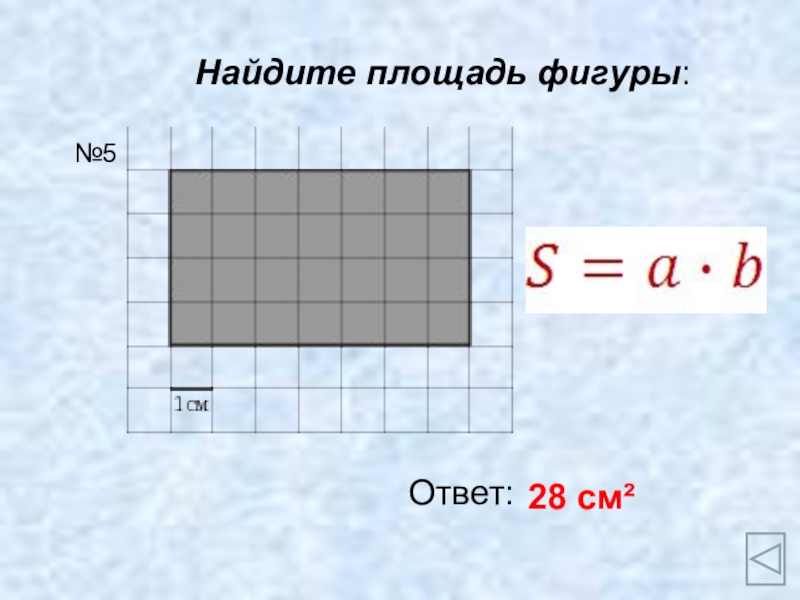
- 7. Найдите площадь фигуры:Ответ:28 см²№5
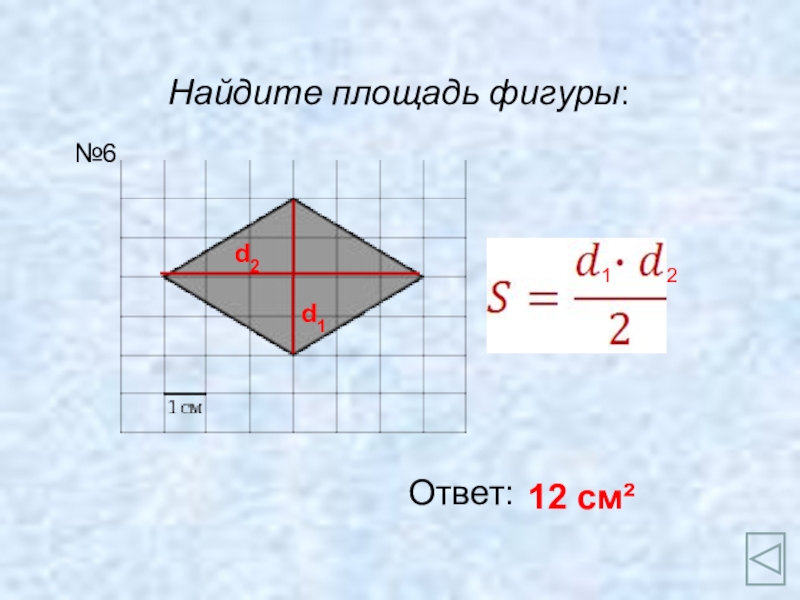
- 8. Найдите площадь фигуры:Ответ:12 см²№6d1d2
- 9. Найдите площадь фигуры:Ответ:17,5 см²№7abh
- 10. Найдите площадь фигуры:Ответ:32, 5 см²№8
- 11. Найдите площадь фигуры:Ответ:15 см²№9
- 12. Найдите площадь фигуры:Ответ:12 см²№10
- 13. Найдите площадь фигуры:Ответ:6 см²№11
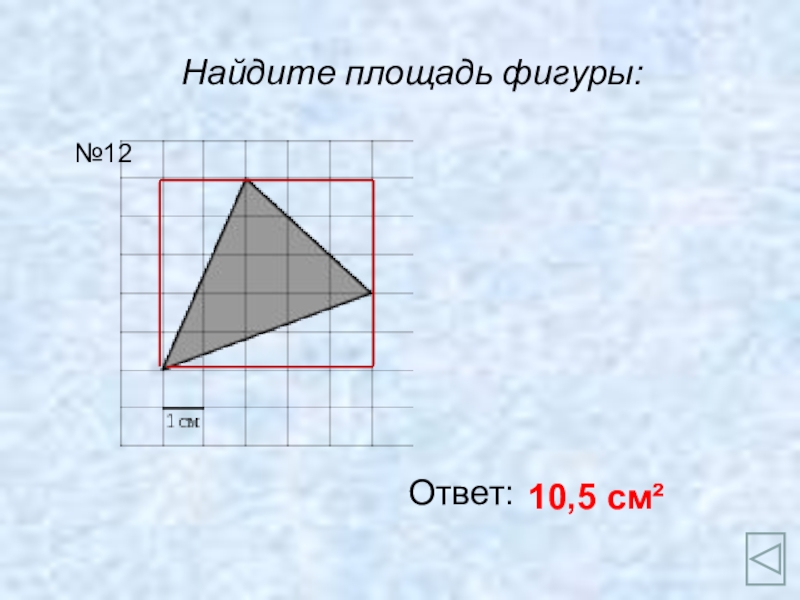
- 14. Найдите площадь фигуры:Ответ:10,5 см²№12
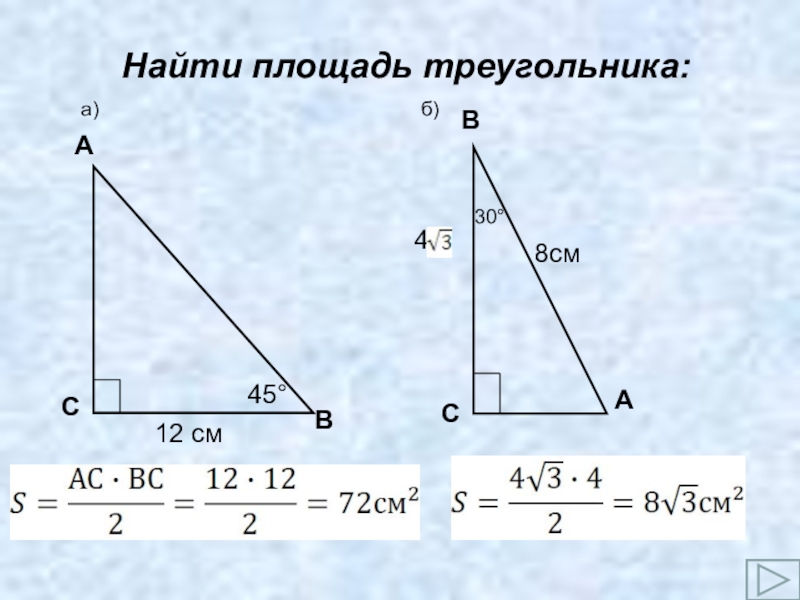
- 15. Найти площадь треугольника:
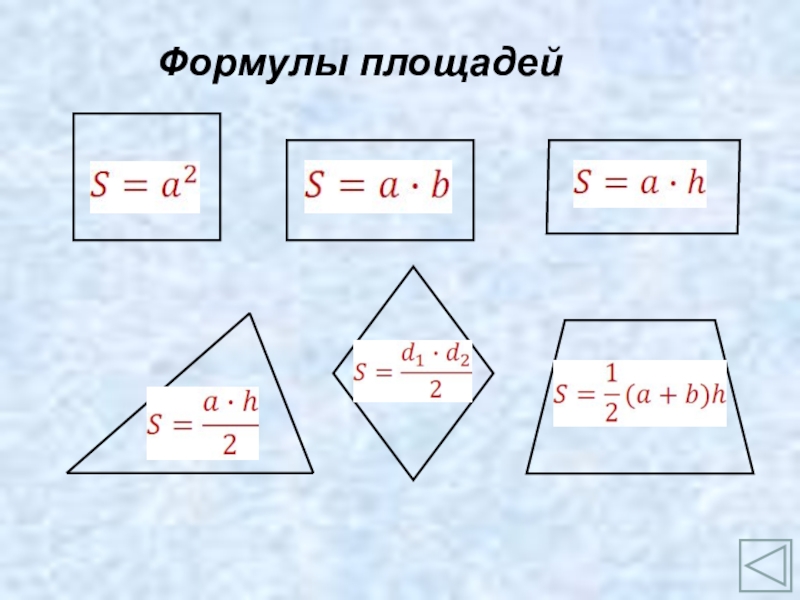
- 16. Формулы площадей
- 17. Задачи урока:закрепить навыки вычисления площади фигур по
- 18. 1. В треугольнике АВС ∠С = 135°,
- 19. № 463Дано: АВСД - параллелограммДАВД= 14 см,
- 20. № 482Дано:АВСД – равн. трапецияНайти: SАВСДРешение:1. Из
Вычисление площадей фигур на клетчатой бумаге123456789101112
Слайд 1Решение задач по теме «Площадь параллелограмма, треугольника, трапеции»
Шаляпина Галина Ивановна учитель
математики МБОУ «Нижнекулойская средняя общеобразовательная школа» Верховажского района Вологодской области
Слайд 17Задачи урока:
закрепить навыки вычисления площади фигур по формуле
научиться применять изученные свойства
фигур для решения задач на вычисление площади
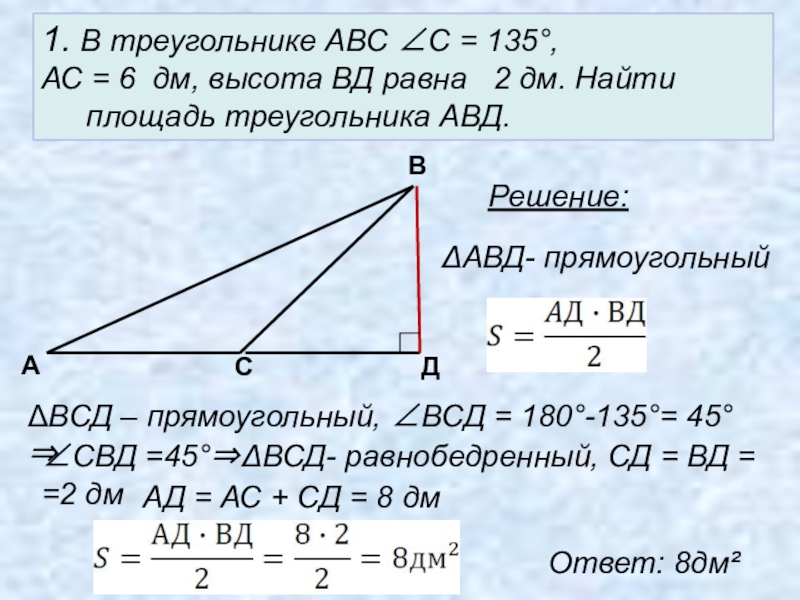
Слайд 181. В треугольнике АВС ∠С = 135°,
АС = 6 дм,
высота ВД равна 2 дм. Найти площадь треугольника АВД.
Решение:
ΔАВД- прямоугольный
ΔВСД – прямоугольный, ∠ВСД = 180°-135°= 45° ⇒
∠СВД =45°⇒ΔВСД- равнобедренный, СД = ВД = =2 дм
АД = АС + СД = 8 дм
Ответ: 8дм²
Слайд 19№ 463
Дано:
АВСД - параллелограмм
Д
А
ВД= 14 см, ДС = 8,1 см
∠ВДС
= 30°
Найти :
SАВСД
30°
Решение:
1. Из вершины В проведём высоту на продолжение стороны ДС
2. SАВСД = ДС∙ВН
3.ΔВДН – прямоугольный, ∠ВДС = 30°⇒
SАВСД = ДС∙ВН =8,1∙ 7 = 56,7 см²
Ответ: 56,7 см²
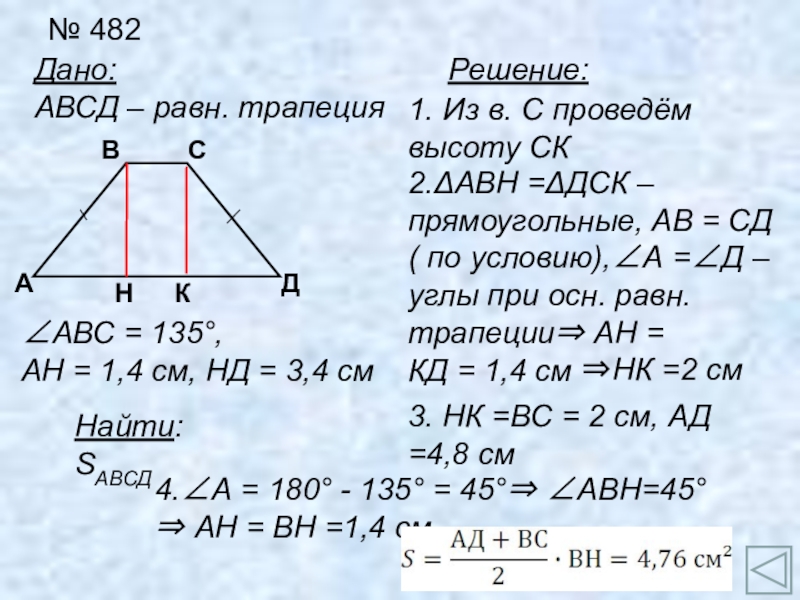
Слайд 20№ 482
Дано:
АВСД – равн. трапеция
Найти:
SАВСД
Решение:
1. Из в. С проведём высоту
СК
2.ΔАВН =ΔДСК – прямоугольные, АВ = СД
( по условию),∠А =∠Д – углы при осн. равн. трапеции⇒ АН =
КД = 1,4 см
⇒НК =2 см
3. НК =ВС = 2 см, АД =4,8 см
4.∠А = 180° - 135° = 45°⇒ ∠АВН=45° ⇒ АН = ВН =1,4 см
