- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение задач на применение теоремы Пифагора и обратной ей теореме
Содержание
- 1. Решение задач на применение теоремы Пифагора и обратной ей теореме
- 2. Пифагор Самосский Пифагор Самосский (ок.
- 3. Решение задач на применение теоремы Пифагора и
- 4. Задача (проверка домашнего задания)
- 5. РешениеДополнительное построениеАН DC; BK
- 6. - Сформулируйте теорему Пифагора
- 7. Самостоятельная работа Определите углы треугольника со сторонами
- 8. ПРОВЕРКАВариант №1Вариант №21²=1 => (
- 9. РЕШЕНИЕ ЗАДАЧ Задача. В некоторой трапеции диагональ
- 10. Задача 494 Дано: ABCD – ромб,
- 11. Задача (дополнительно в случае быстрого решения двух
- 12. Итоги урокаДомашнее задание: 495 (б), 496, 518
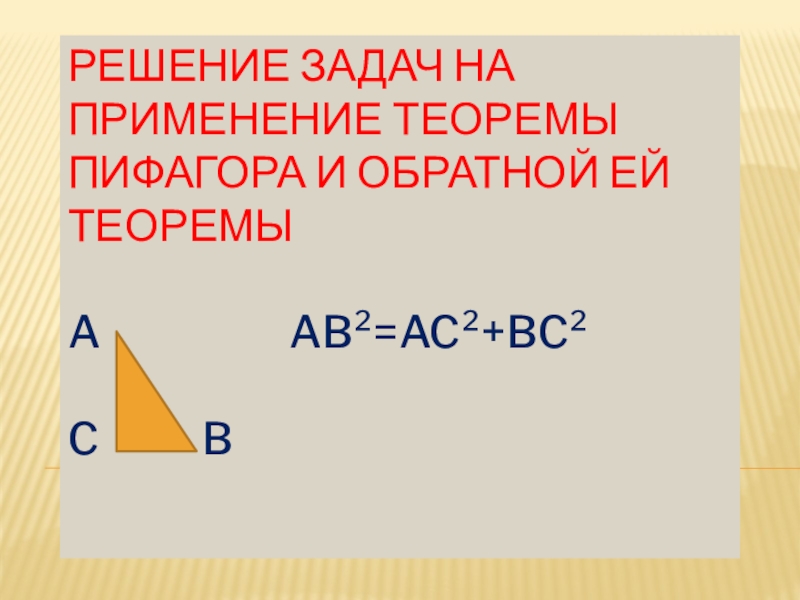
Слайд 1ТЕМА УРОКА
Решение задач на применение теоремы Пифагора и обратной ей теоремы
Учитель
ГБОУ школа № 212 Санкт-Петербург
Ратюк Елена Ивановна
Слайд 2Пифагор Самосский
Пифагор Самосский (ок. 580 — ок. 500
Пифагор со своими учениками впервые придал геометрии научный характер. Кроме своей главной теоремы, известной любому современному школьнику, Пифагору отметился доказательством теоремы о сумме углов треугольника; задачей о покрытии плоскости правильными многоугольниками. Также ему принадлежат геометрические способы нахождения корней квадратных уравнений, алгоритмы решения задачи о том, как по двум данным на плоскости фигурам построить третью, равновеликую одной из них ( то есть имеющую с ней равную площадь) и подобную другой.
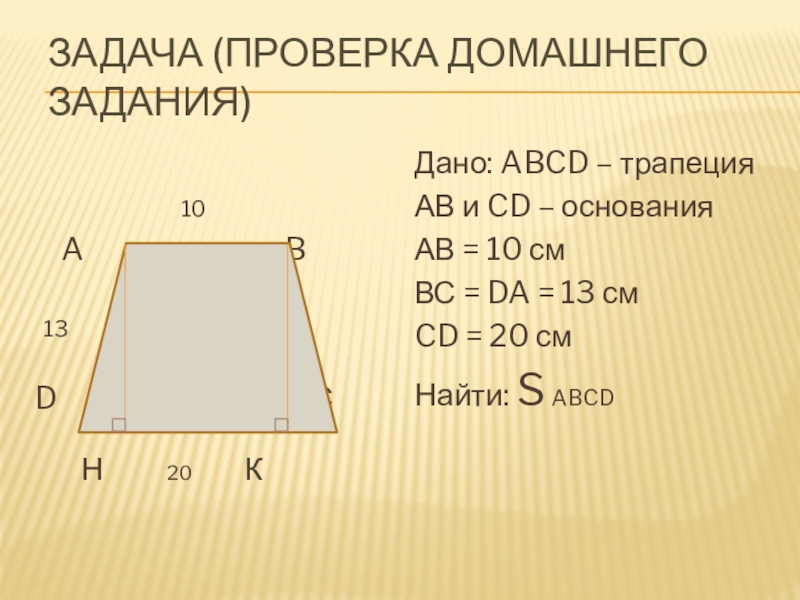
Слайд 4Задача (проверка домашнего задания)
10
A
13
D С
Н 20 К
Дано: ABCD – трапеция
АВ и CD – основания
АВ = 10 см
ВС = DA = 13 см
CD = 20 см
Найти: S ABCD
Слайд 5Решение
Дополнительное построение
АН DC; BK DC
1) Рассмотрим
= > ∆ ADH=∆ BCK (по гипотенузе и катету)
Т.о. DH=KC = > 2DH=20-10
HK=AB=10 cм DH=5 см
По теореме Пифагора: AD²=AH² + DH² = >
AH ²= 13 ²+5 ²=144
AH=12 см
2) SABCD = ⅟2(AB+DC)AH
SABCD = ⅟2(10+20)12 = 180 см ²
Ответ: SABCD = 180 см ²
Слайд 7Самостоятельная работа
Определите углы треугольника со сторонами
1 вариант
1 ; 1 ;
2 вариант
1 ; ; 2
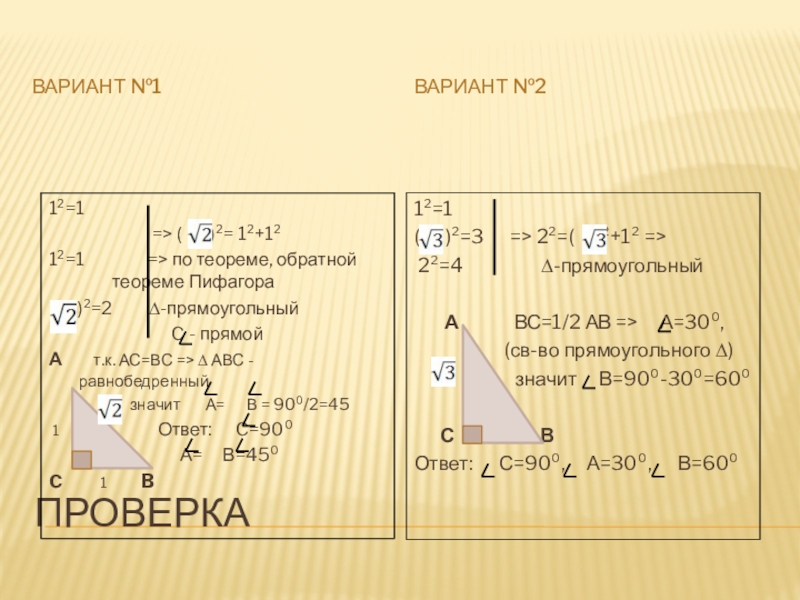
Слайд 8ПРОВЕРКА
Вариант №1
Вариант №2
1²=1
=> ( )²=
1²=1 => по теореме, обратной теореме Пифагора
( )²=2 ∆-прямоугольный
C - прямой
А т.к. АС=ВС => ∆ АВС - равнобедренный
значит А= В = 90⁰/2=45
1 Ответ: C=90⁰
1 А= В=45⁰
C 1 B
1²=1
( )²=3 => 2²=( )²+1² =>
2²=4 ∆-прямоугольный
А ВС=1/2 АВ => А=30⁰,
(св-во прямоугольного ∆)
значит В=90⁰-30⁰=60⁰
С В
Ответ: С=90⁰, А=30⁰, В=60⁰
Слайд 9РЕШЕНИЕ ЗАДАЧ
Задача. В некоторой трапеции диагональ и боковая сторона, выходящие
Дано: ABCD – трапеция
7 см АВ = см, ВН AD, ВН=24см,
В С BD=26 см, ВС=7 см.
262 SABCD=?
Решение:
А D SABCD=1/2(BC+AD)AH,
AD=AH+HD, ∆ ABH - прямоугольный,
АВ²=ВН²+HD² => (AH)² = ( )²-24²=1, AH=1 см
∆ BDH – прямоугольный, BD²=BH²+HD² => HD²=26²-24²=676-576=100 =>
HD=10 см, т.о. AD=1+10=11 см;
SABCD= (7+11)x24 = 216 cм² Ответ: SABCD=216 см²
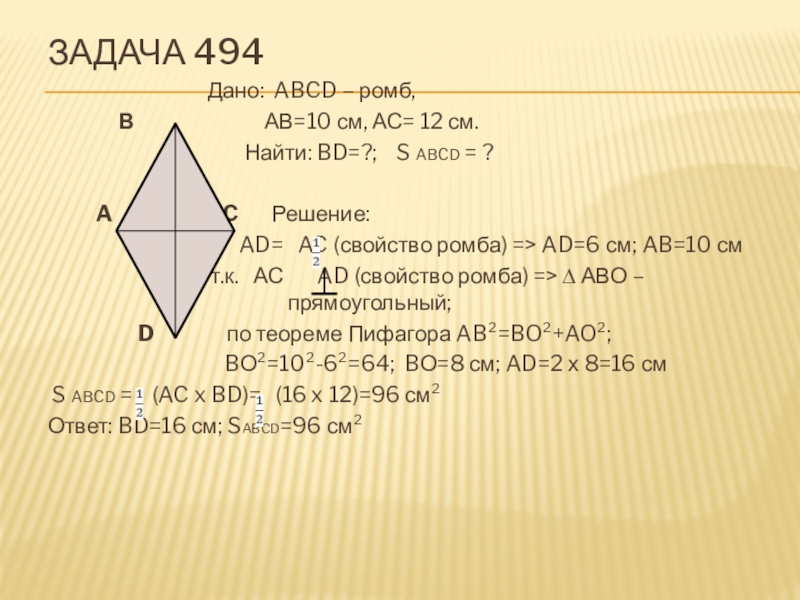
Слайд 10Задача 494
Дано: ABCD – ромб,
Найти: BD=?; S ABCD = ?
A C Решение:
AD= AC (свойство ромба) => AD=6 см; AB=10 см
т.к. АС AD (свойство ромба) => ∆ АВО – прямоугольный;
D по теореме Пифагора AB²=BO²+AO²;
BО²=10²-6²=64; BО=8 см; AD=2 х 8=16 см
S ABCD = (AC x BD)= (16 x 12)=96 см²
Ответ: BD=16 см; SABCD=96 см²
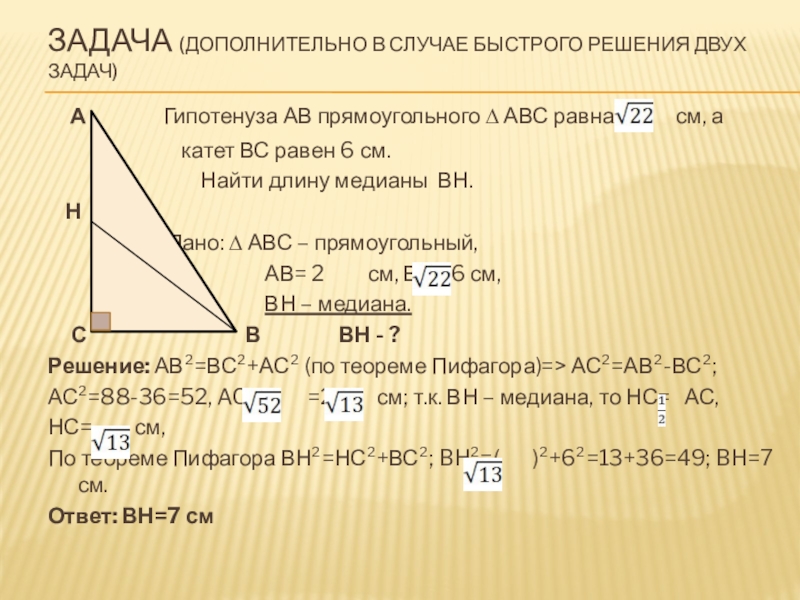
Слайд 11Задача (дополнительно в случае быстрого решения двух задач)
А
катет ВС равен 6 см.
Найти длину медианы ВН.
Н
Дано: ∆ АВС – прямоугольный,
АВ= 2 см, ВС= 6 см,
ВН – медиана.
С В ВН - ?
Решение: АВ²=ВС²+АС² (по теореме Пифагора)=> АС²=АВ²-ВС²;
АС²=88-36=52, AC= =2 см; т.к. ВН – медиана, то НС= АС,
НС= см,
По теореме Пифагора ВН²=НС²+ВС²; BH²=( )²+6²=13+36=49; BH=7 см.
Ответ: ВН=7 см