- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение задач. Метод координат
Содержание
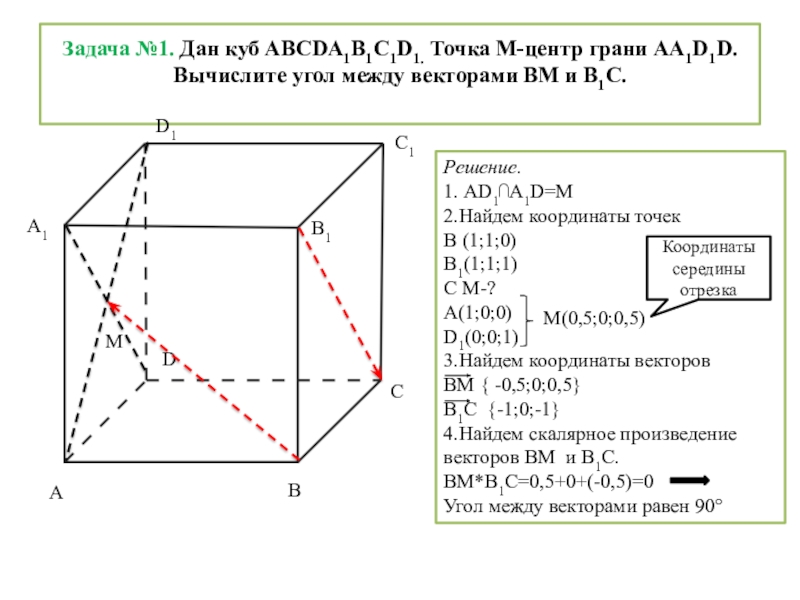
Слайд 2Задача №1. Дан куб ABCDA1B1C1D1. Точка М-центр грани AA1D1D. Вычислите угол
А
D
С
В
B1
A1
C1
D1
M
Решение.
1. АD1⋂A1D=М
2.Найдем координаты точек
В (1;1;0)
B1(1;1;1)
С М-?
А(1;0;0)
D1(0;0;1)
3.Найдем координаты векторов
ВМ { -0,5;0;0,5}
B1C {-1;0;-1}
4.Найдем скалярное произведение векторов ВМ и B1C.
ВМ*B1C=0,5+0+(-0,5)=0
Угол между векторами равен 90°
М(0,5;0;0,5)
Координаты середины отрезка
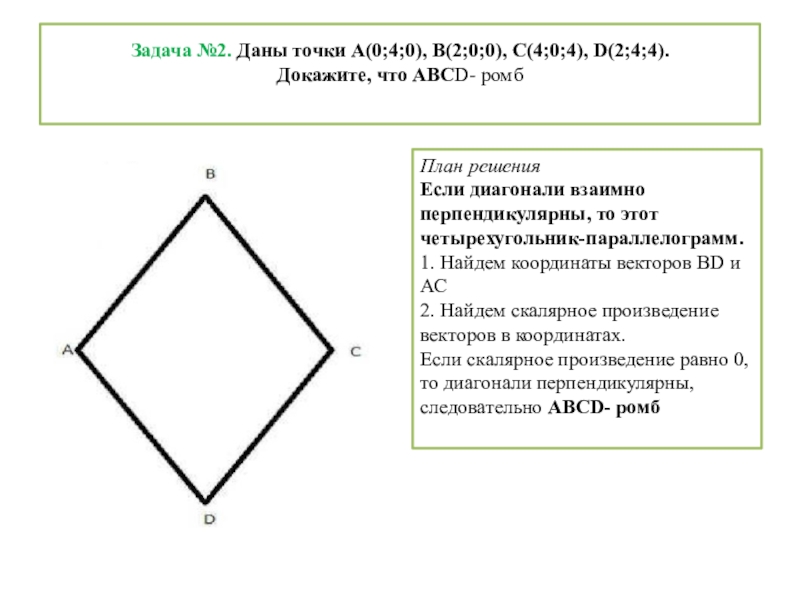
Слайд 3 Задача №2. Даны точки А(0;4;0), В(2;0;0), С(4;0;4), D(2;4;4). Докажите, что АВСD- ромб
План решения
Если диагонали взаимно перпендикулярны, то этот четырехугольник-параллелограмм.
1. Найдем координаты векторов ВD и АС
2. Найдем скалярное произведение векторов в координатах.
Если скалярное произведение равно 0, то диагонали перпендикулярны, следовательно АВСD- ромб
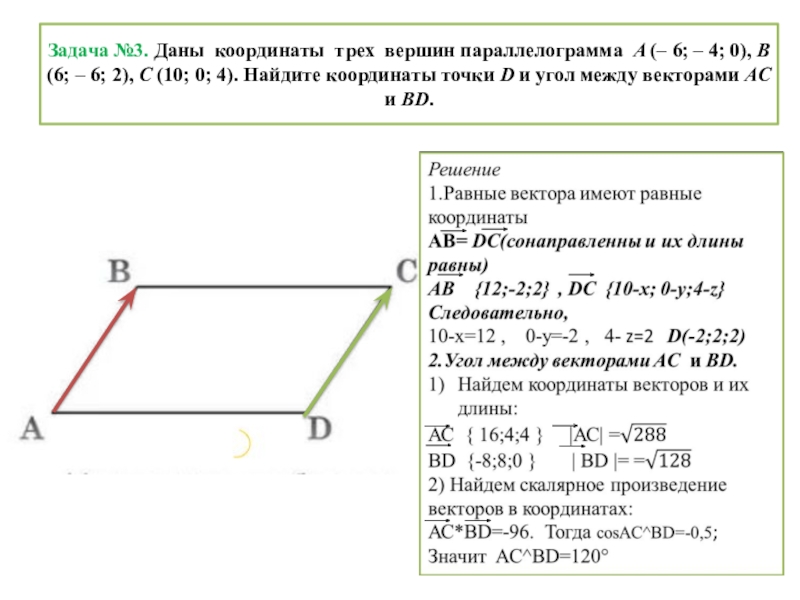
Слайд 4 Задача №3. Даны координаты трех вершин параллелограмма A (– 6; –
Слайд 5 Задача №4. Даны векторы a {1; 2; – 1}, b{–
Правила
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Ответ. -20
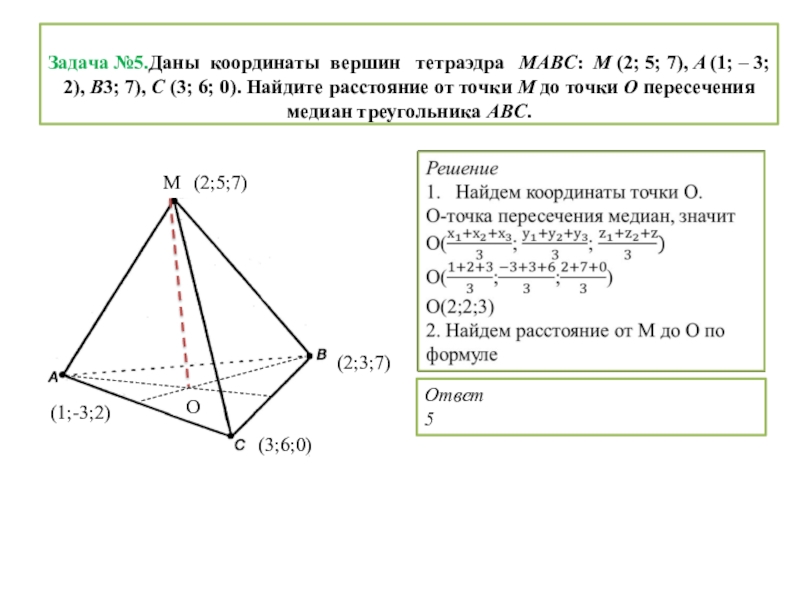
Слайд 6 Задача №5.Даны координаты вершин тетраэдра MABC: M (2; 5;
М
(2;5;7)
(1;-3;2)
(3;6;0)
(2;3;7)
О
Ответ
5