- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение задач геометрического содержания на координатной плоскости с опорой на графические представления
Содержание
- 1. Решение задач геометрического содержания на координатной плоскости с опорой на графические представления
- 2. Задача № 1.Найдите все значения k, при
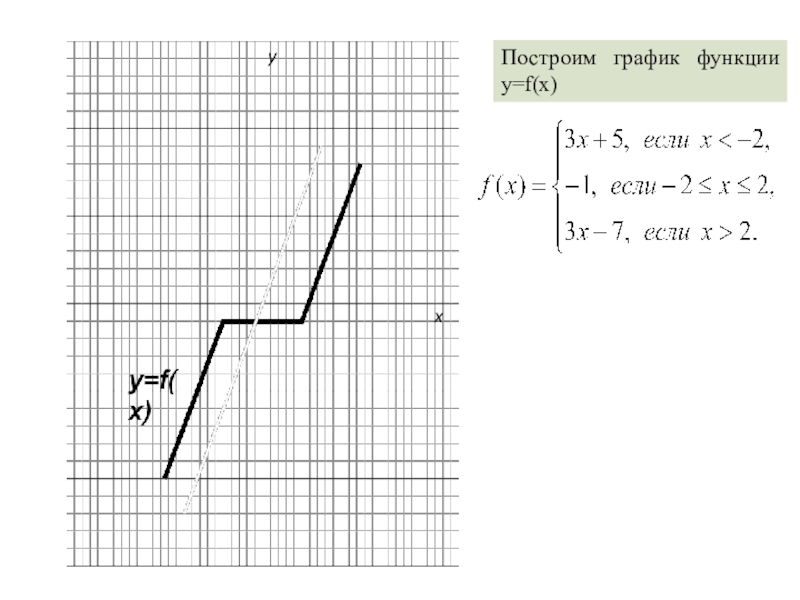
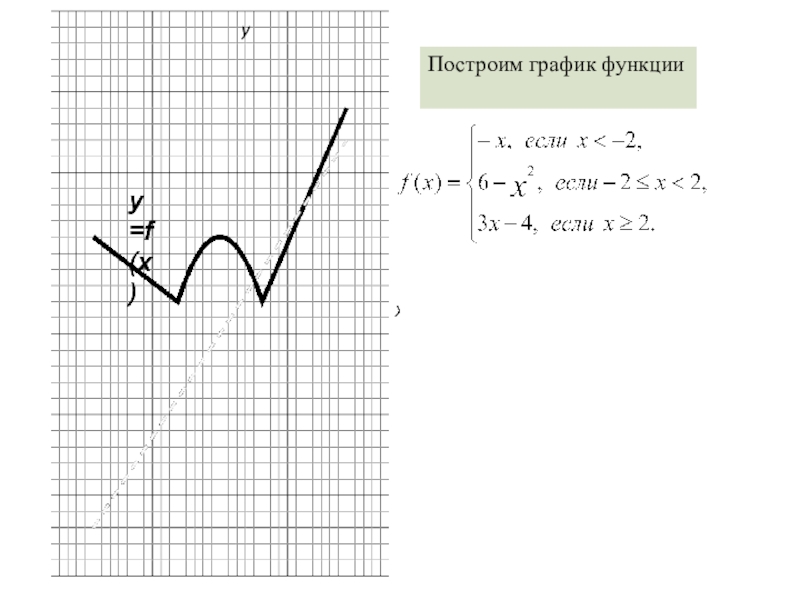
- 3. yxПостроим график функции y=f(x)
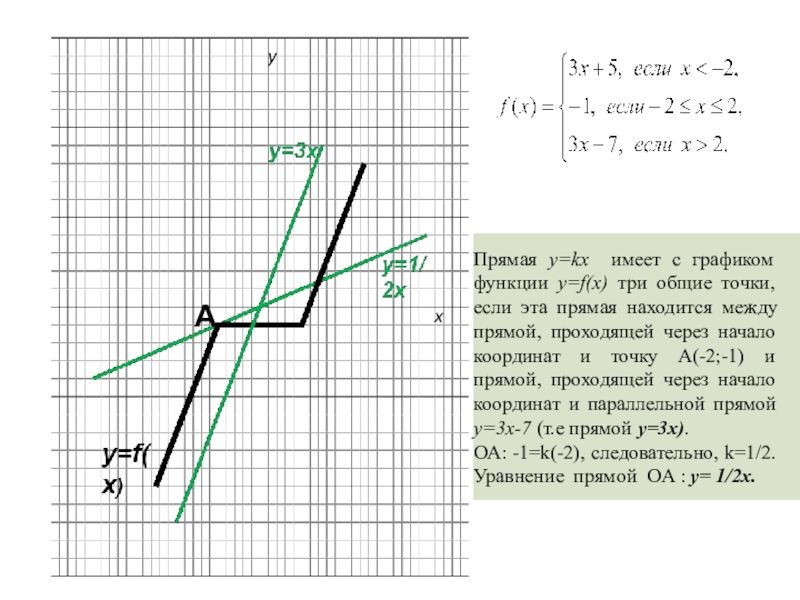
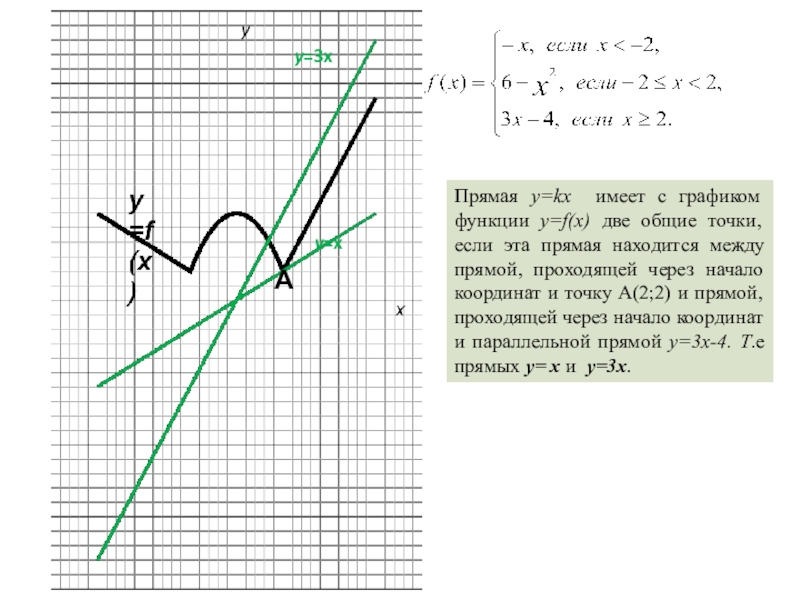
- 4. yxПрямая y=kx имеет с графиком функции y=f(x)
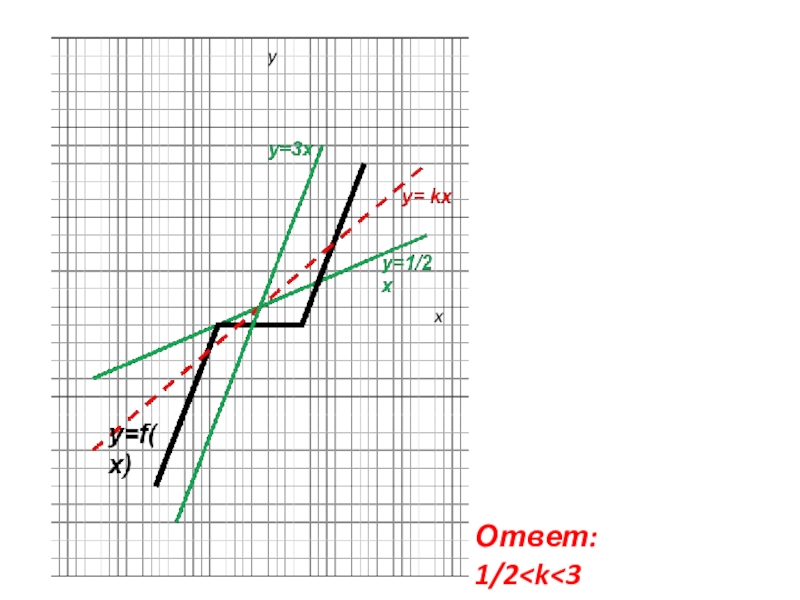
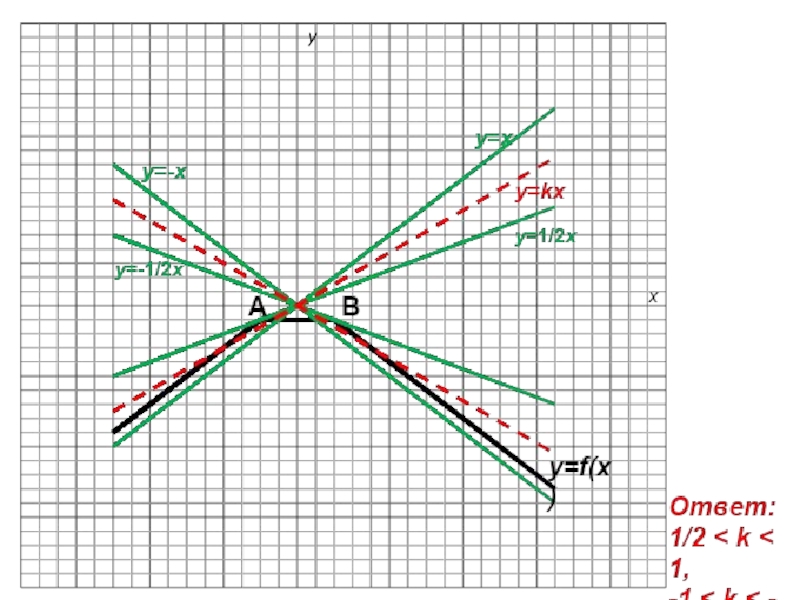
- 5. Ответ: 1/2
- 6. Задача № 2.Найдите все значения k, при
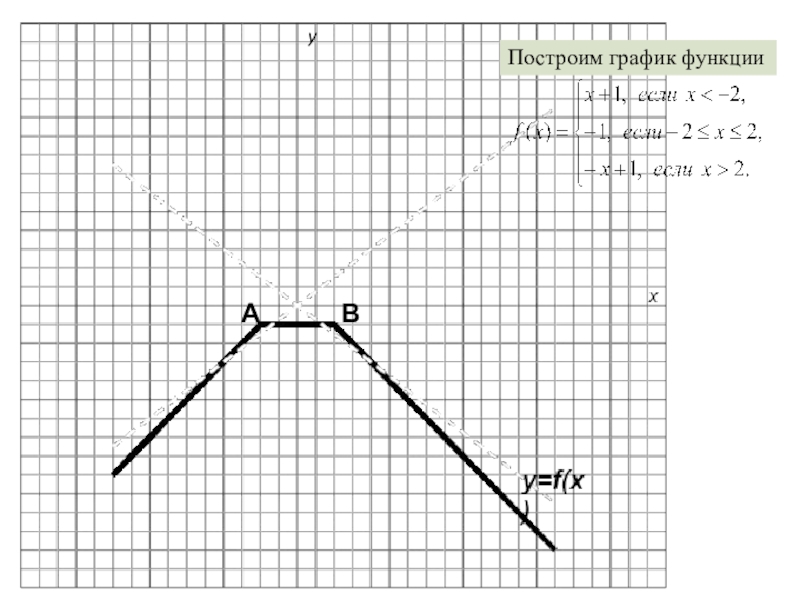
- 7. yАВПостроим график функции
- 8. yИскомая прямая должна лежать между прямой ОА
- 9. y
- 10. Задача № 3.В окружности с центром в
- 11. y=2/3xxyПрямые ОА, ОК и ОD имеют ровно
- 12. y=2/3xy=2/5xxyПрямые ОВ, ОС пересекают диаметры окружности в
- 13. Задача № 4.Найдите все значения k, при
- 14. yПостроим график функции
- 15. y=xy=3xyПрямая y=kx имеет с графиком функции y=f(x)
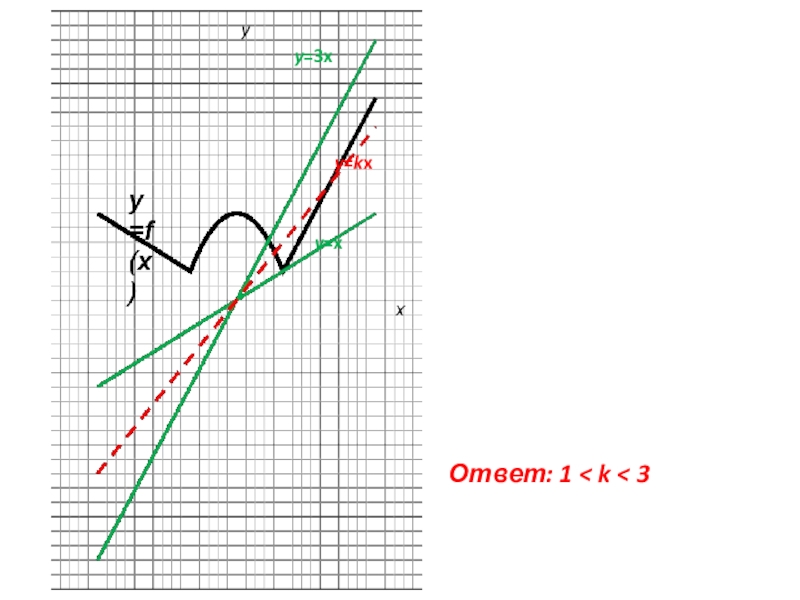
- 16. y=xy=3xy=kxОтвет: 1 < k < 3y
- 17. Задача № 5.Найдите все значения m, при которых уравнение ||x-5|-3|= mx имеет не менее трёх корней.
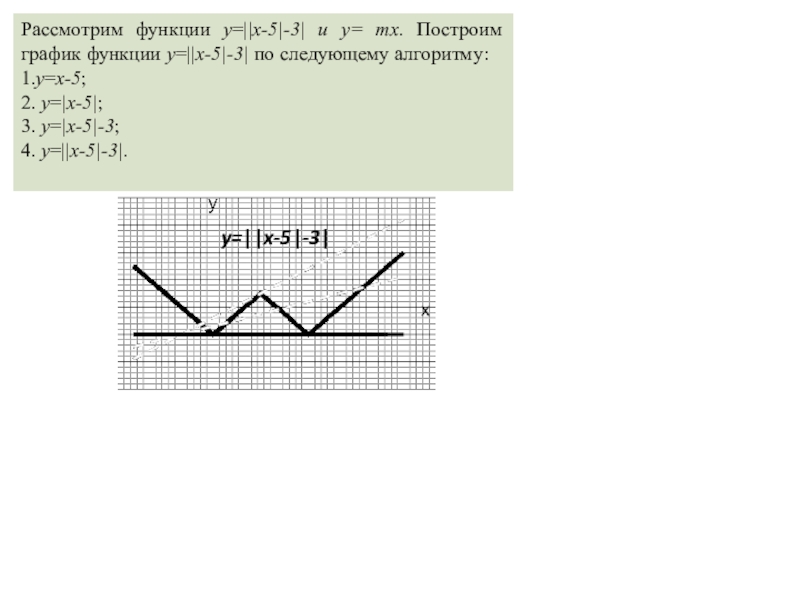
- 18. y=||x-5|-3|xРассмотрим функции y=||x-5|-3| и y= mx. Построим график функции y=||x-5|-3| по следующему алгоритму:1.y=x-5;2. y=|x-5|;3. y=|x-5|-3;4. y=||x-5|-3|.
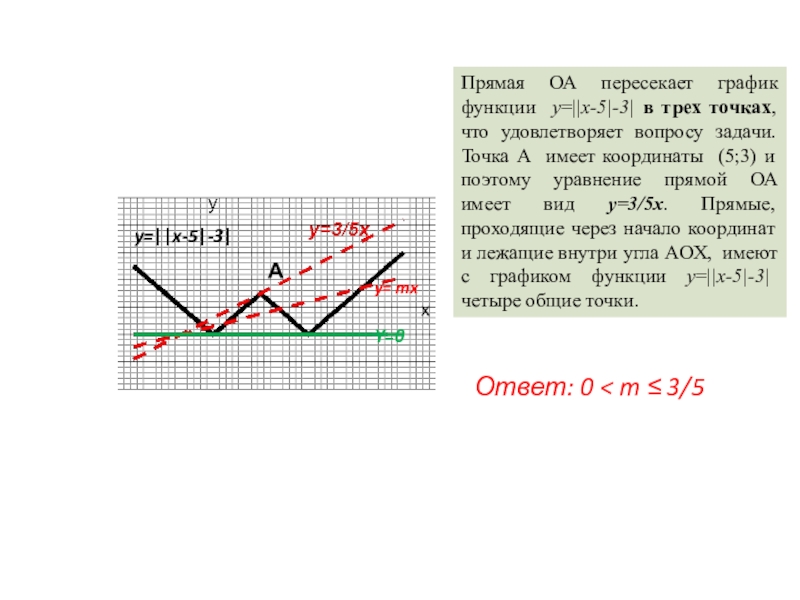
- 19. y= mxОтвет: 0 < m ≤ 3/5Y=0y=||x-5|-3|xАПрямая
- 20. Задача № 6Найдите количество точек с целыми
- 21. Построим график функции
- 22. x=1
- 23. Построим график функции
- 24. xy
- 25. y=f(x)Ответ: 22 точки с целочисленными координатами расположены ниже параболы и выше ломаной.yx
Задача № 1.Найдите все значения k, при которых прямая y=kx пересекает в трех различных точках график функции у = f(x), где
Слайд 1Решение задач геометрического содержания на координатной плоскости с опорой на графические
представления.
(ГИА. Алгебра 9.
Задача № 23)
Слайд 2Задача № 1.
Найдите все значения k, при которых прямая
y=kx пересекает
в трех различных точках график функции у = f(x), где
Слайд 4y
x
Прямая y=kx имеет с графиком функции y=f(x) три общие точки, если
эта прямая находится между прямой, проходящей через начало координат и точку А(-2;-1) и прямой, проходящей через начало координат и параллельной прямой y=3x-7 (т.е прямой y=3x).
ОА: -1=k(-2), следовательно, k=1/2. Уравнение прямой OA : y= 1/2x.
ОА: -1=k(-2), следовательно, k=1/2. Уравнение прямой OA : y= 1/2x.
А
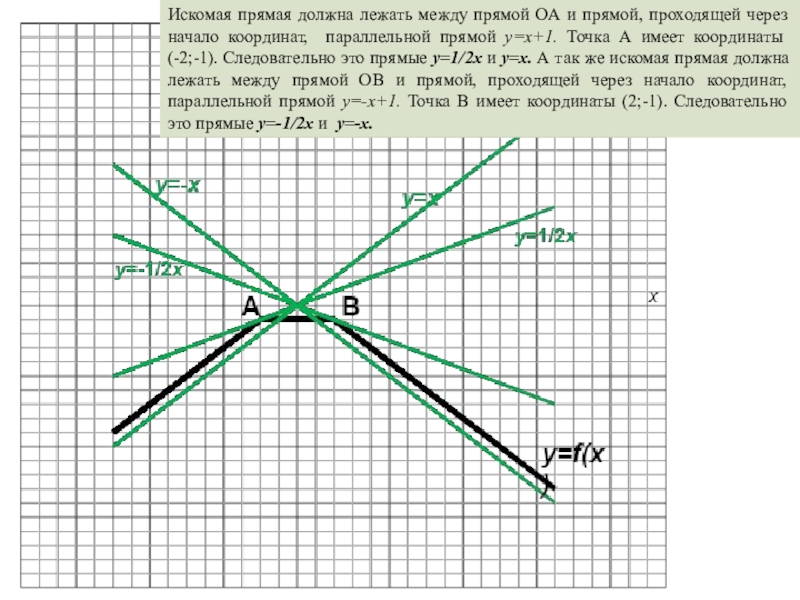
Слайд 6Задача № 2.
Найдите все значения k, при которых прямая y= kx
пересекает в двух различных точках график функции у = f(x), где
Слайд 8y
Искомая прямая должна лежать между прямой ОА и прямой, проходящей через
начало координат, параллельной прямой y=x+1. Точка А имеет координаты (-2;-1). Следовательно это прямые y=1/2x и y=x. А так же искомая прямая должна лежать между прямой ОВ и прямой, проходящей через начало координат, параллельной прямой y=-x+1. Точка В имеет координаты (2;-1). Следовательно это прямые y=-1/2x и y=-x.
Слайд 10Задача № 3.
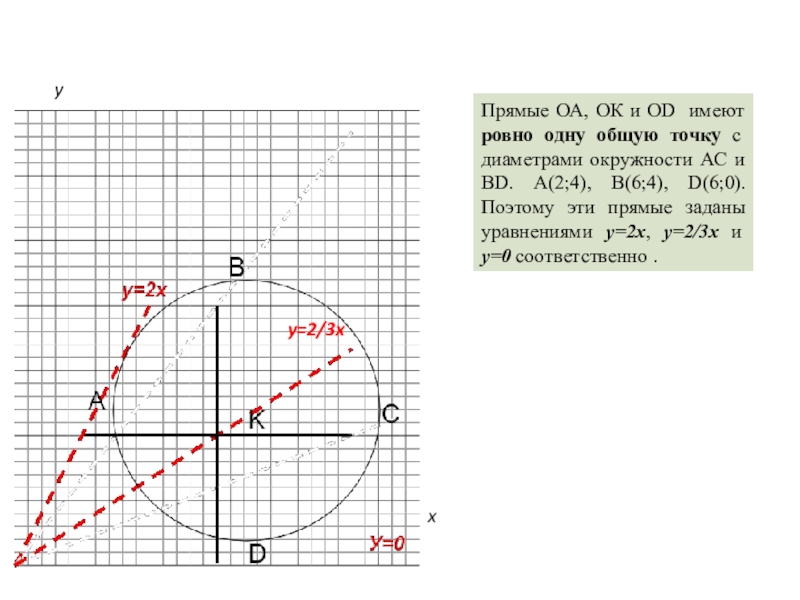
В окружности с центром в точке К(6;4) и радиусом
4 проведены два диаметра, параллельно осям координат. Найдите все значения k, при которых прямая y= kx имеет ровно одну общую точку с диаметрами.
Слайд 11y=2/3x
x
y
Прямые ОА, ОК и ОD имеют ровно одну общую точку с
диаметрами окружности АС и ВD. А(2;4), В(6;4), D(6;0). Поэтому эти прямые заданы уравнениями y=2x, y=2/3x и y=0 соответственно .
Слайд 12y=2/3x
y=2/5x
x
y
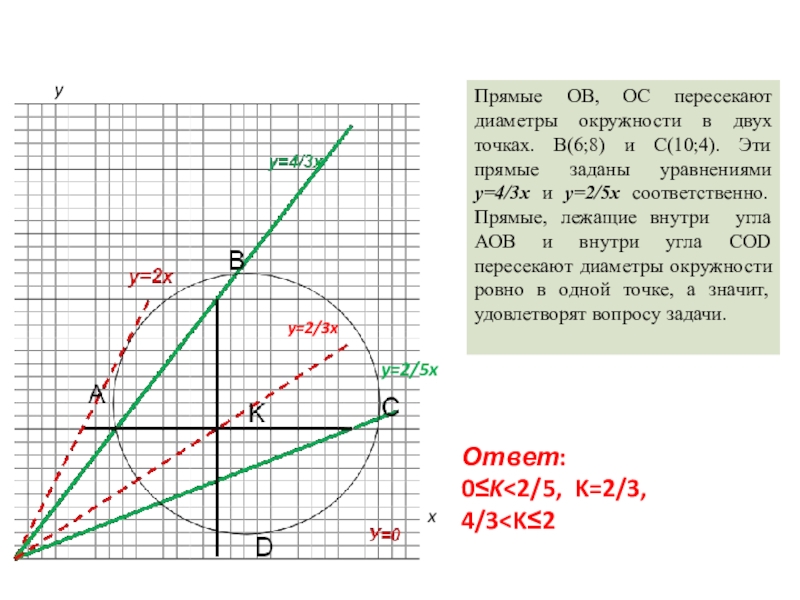
Прямые ОВ, ОС пересекают диаметры окружности в двух точках. В(6;8) и
С(10;4). Эти прямые заданы уравнениями y=4/3x и y=2/5x соответственно. Прямые, лежащие внутри угла АОВ и внутри угла СОD пересекают диаметры окружности ровно в одной точке, а значит, удовлетворят вопросу задачи.
Ответ:
0≤K<2/5, K=2/3, 4/3
Слайд 13Задача № 4.
Найдите все значения k, при которых прямая
y=kx пересекает
в двух различных точках график функции у = f(x), где
Слайд 15y=x
y=3x
y
Прямая y=kx имеет с графиком функции y=f(x) две общие точки, если
эта прямая находится между прямой, проходящей через начало координат и точку А(2;2) и прямой, проходящей через начало координат и параллельной прямой y=3x-4. Т.е прямых y= x и y=3x.
А
Слайд 17Задача № 5.
Найдите все значения m, при которых уравнение ||x-5|-3|= mx
имеет не менее трёх корней.
Слайд 18y=||x-5|-3|
x
Рассмотрим функции y=||x-5|-3| и y= mx. Построим график функции y=||x-5|-3| по
следующему алгоритму:
1.y=x-5;
2. y=|x-5|;
3. y=|x-5|-3;
4. y=||x-5|-3|.
1.y=x-5;
2. y=|x-5|;
3. y=|x-5|-3;
4. y=||x-5|-3|.
Слайд 19y= mx
Ответ: 0 < m ≤ 3/5
Y=0
y=||x-5|-3|
x
А
Прямая ОА пересекает график функции
y=||x-5|-3| в трех точках, что удовлетворяет вопросу задачи. Точка А имеет координаты (5;3) и поэтому уравнение прямой ОА имеет вид y=3/5x. Прямые, проходящие через начало координат и лежащие внутри угла AOX, имеют с графиком функции y=||x-5|-3| четыре общие точки.
Слайд 20Задача № 6
Найдите количество точек с целыми координатами, расположенными ниже параболы
и выше ломаной, заданной условиями:
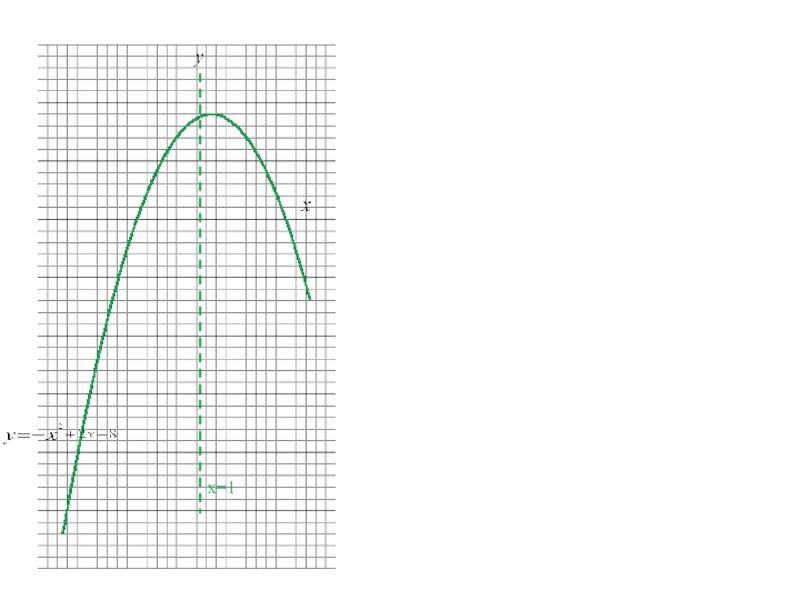
Слайд 21Построим график функции
. Графиком является парабола, ветви которой направлены вниз.
Точка А(x0;y0) является вершиной параболы.
x0= -b/2a, x0=1, y0=y(x0), y0=-1+2+8=9. A(1;9).
x=1 – уравнение оси параболы.
Дополнительные точки
Точка А(x0;y0) является вершиной параболы.
x0= -b/2a, x0=1, y0=y(x0), y0=-1+2+8=9. A(1;9).
x=1 – уравнение оси параболы.
Дополнительные точки
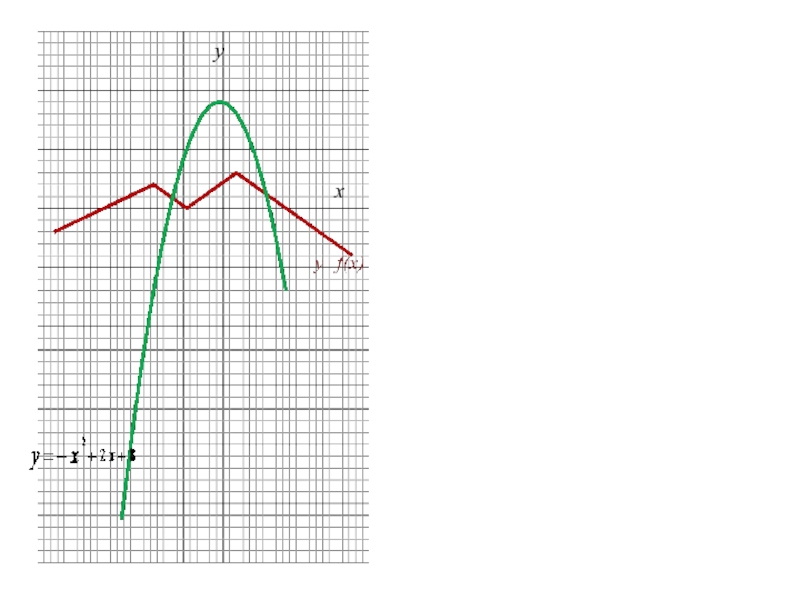
Слайд 23Построим график функции
Графиком функции является прямая, проходящая через точки (-3; 2) и (-9;-2). Выделим часть прямой для x<-3.
. Построим сначала график функции y=x+1. Затем часть графика, лежащую ниже оси x отобразим симметрично относительно оси x . Выделим часть графика для -3 ≤ x < 2.
Графиком функции y=-x+5 является прямая. Построим ее с помощью прямой y=-x путем перемещения вверх вдоль оси y на 5 единичных отрезков. Выделим часть прямой для x ≥ 2.
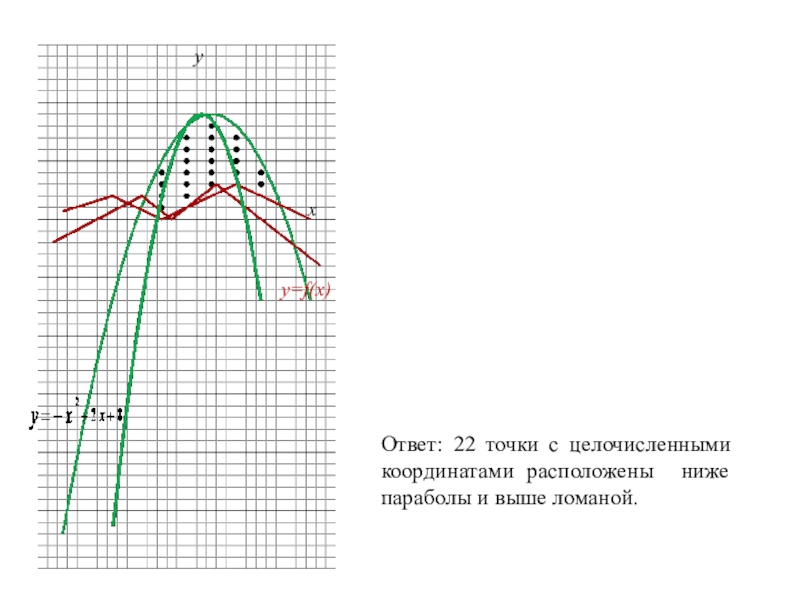
Слайд 25y=f(x)
Ответ: 22 точки с целочисленными координатами расположены ниже параболы и выше
ломаной.
y
x