- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Разработка урока по геометрии Решение задач по теме векторы
Содержание
- 1. Разработка урока по геометрии Решение задач по теме векторы
- 2. Систематизировать знания , умения и навыки учащихся
- 3. аb3b½аНачертить два неколлинеарных вектора а и b.
- 4. На стороне ВС ромба АВСD лежит
- 5. В равнобедренной трапеции высота делит большее основание
- 6. В равнобедренной трапеции один из углов равен
- 7. Дано: ABCD- квадрат. АВ=а, АС=bНайти: ВО, ВР,
- 8. Дано: ABCD- квадрат. АВ=а, АС=bНайти: ВО, ВЕРешение:
- 9. Дано: ABCD- параллелограмм. BК=КC, СЕ:ЕD=2:3.Найти: АК, АЕ,
- 10. УСПЕХОВ!
Слайд 2
Систематизировать знания , умения и навыки учащихся по изученной теме.
Совершенствовать навыки
Подготовка учащихся к контрольной работе.
Геометрия приближает разум к истине.
Платон.
Цели урока:
Слайд 3а
b
3b
½а
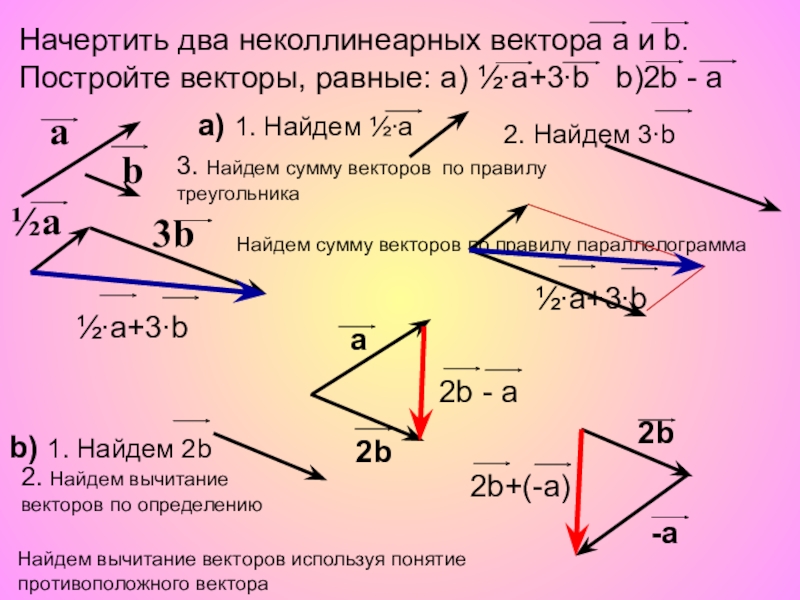
Начертить два неколлинеарных вектора а и b. Постройте векторы, равные: а)
а) 1. Найдем ½∙а
2. Найдем 3∙b
3. Найдем cумму векторов по правилу треугольника
½∙а+3∙b
Найдем cумму векторов по правилу параллелограмма
½∙а+3∙b
b) 1. Найдем 2b
2. Найдем вычитание
векторов по определению
2b
а
2b - а
Найдем вычитание векторов используя понятие противоположного вектора
2b
-а
2b+(-а)
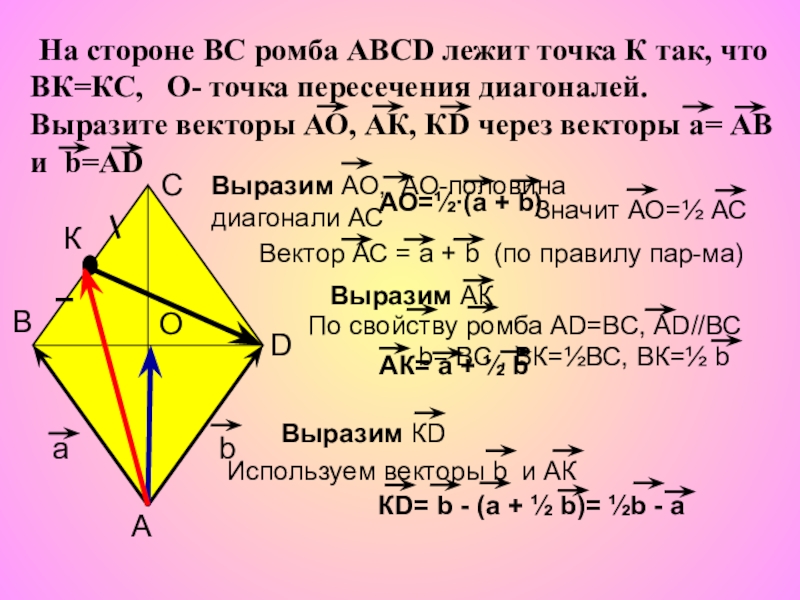
Слайд 4 На стороне ВС ромба АВСD лежит точка К так, что
В
К
D
С
А
О
b
а
Выразим АО, АО-половина
диагонали АС
Вектор АС = а + b (по правилу пар-ма)
Выразим АК
Значит АО=½ АС
По свойству ромба АD=ВС, АD//ВС
b= ВС , ВК=½ВС, ВК=½ b
АК= а + ½ b
Выразим КD
Используем векторы b и АК
КD= b - (а + ½ b)= ½b - a
АО=½∙(а + b)
Слайд 5
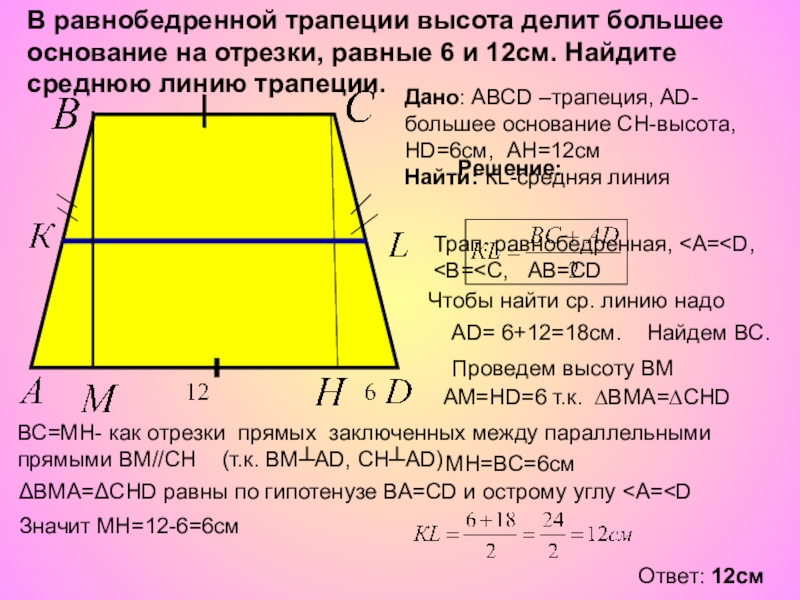
В равнобедренной трапеции высота делит большее основание на отрезки, равные 6
Дано: АВСD –трапеция, АD-большее основание СН-высота, НD=6см, АН=12см
Найти: КL-средняя линия
Трап. равнобедренная, <А= Чтобы найти ср. линию надо АD= 6+12=18cм. ВС=МН- как отрезки прямых заключенных между параллельными прямыми ВМ//CH Проведем высоту ВМ (т.к. ВМ┴АD, СН┴АD) АМ=НD=6 т.к. ∆ВМА=∆СНD ΔВМА=ΔСНD равны по гипотенузе ВА=СD и острому углу <А= Значит МН=12-6=6см МН=ВС=6см Ответ: 12см Найдем ВС. Решение:
Слайд 6
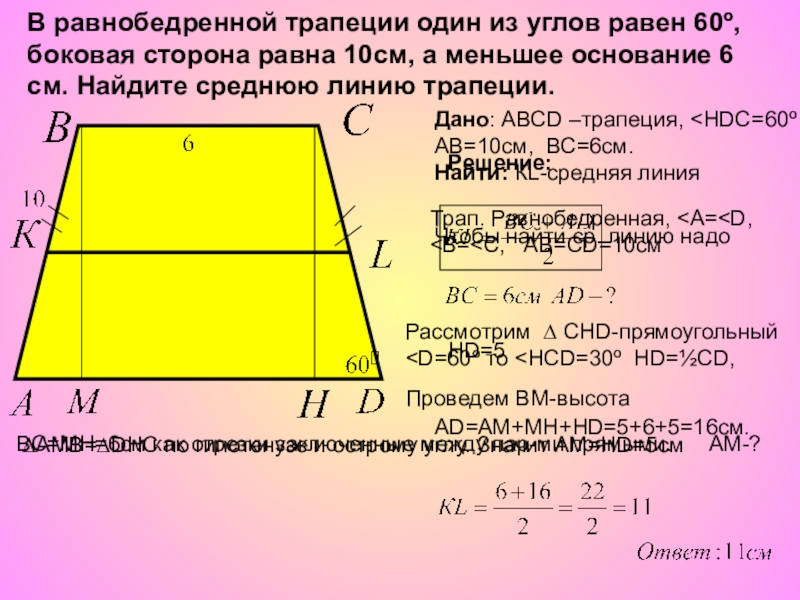
В равнобедренной трапеции один из углов равен 60º, боковая сторона равна
Дано: АВСD –трапеция, <НDC=60º АВ=10см, ВС=6см.
Найти: КL-средняя линия
Трап. Равнобедренная, <А= Чтобы найти ср. линию надо Рассмотрим ∆ СНD-прямоугольный Проведем ВМ-высота ВС=МН=6см как отрезки заключенные между пар-ми прямыми. АМ-? ∆АМВ=∆DHC по гипотенузе и острому углу. Значит АМ=НD=5см AD=АМ+МН+НD=5+6+5=16см. Решение: НD=5
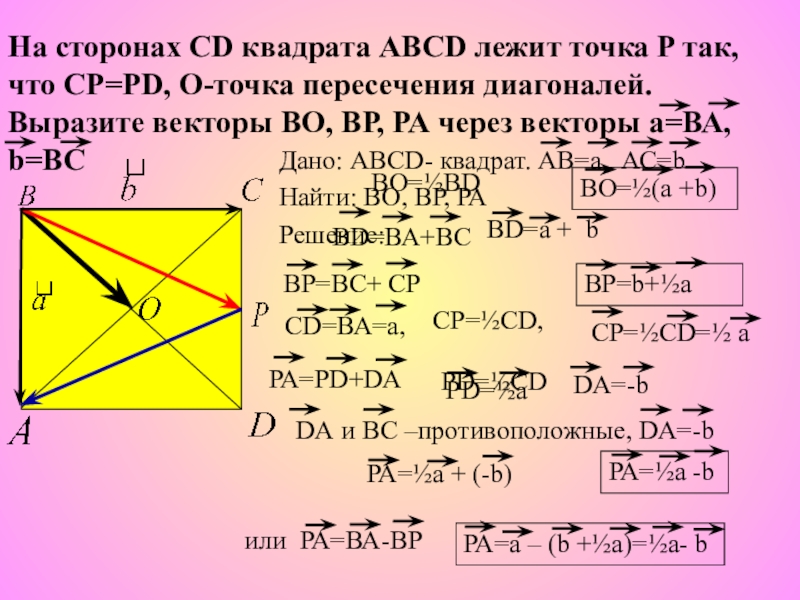
Слайд 7Дано: ABCD- квадрат. АВ=а, АС=b
Найти: ВО, ВР, РА
Решение:
На сторонах СD
ВО=½ВD
ВD=ВА+ВС
ВD=а + b
ВО=½(а +b)
СD=ВА=а,
СР=½СD,
СР=½СD=½ a
BР=ВС+ СР
BР=b+½а
РА=РD+DA
РD=½CD
РD=½а
DА и ВС –противоположные, DA=-b
РА=½а + (-b)
РА=½а -b
или РА=ВА-ВР
РА=а – (b +½а)=½а- b
DA=-b
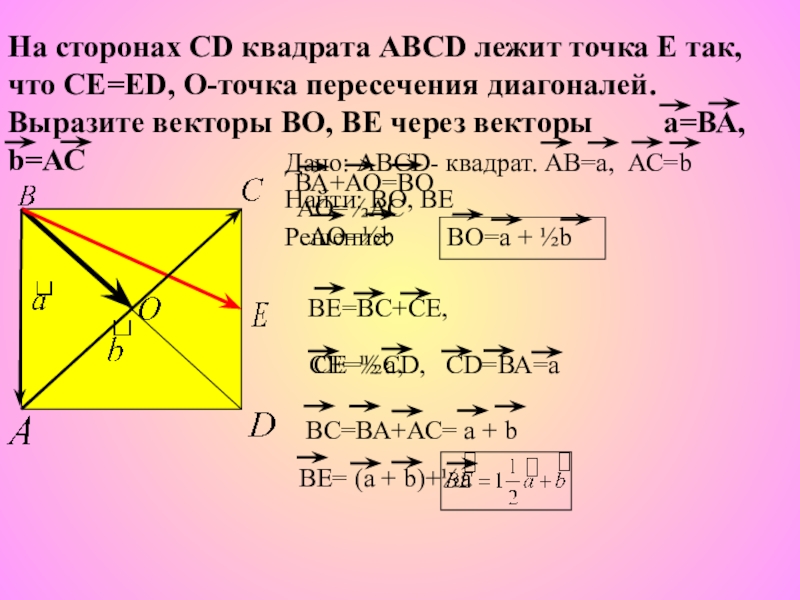
Слайд 8Дано: ABCD- квадрат. АВ=а, АС=b
Найти: ВО, ВЕ
Решение:
На сторонах СD квадрата
АО=½АС
АО=½b
ВА+АО=ВО
ВО=а + ½b
СЕ=½СD, СD=ВА=а
СЕ=½ a,
ВЕ=ВС+СЕ,
ВЕ= (а + b)+½а
ВС=ВА+АС= а + b
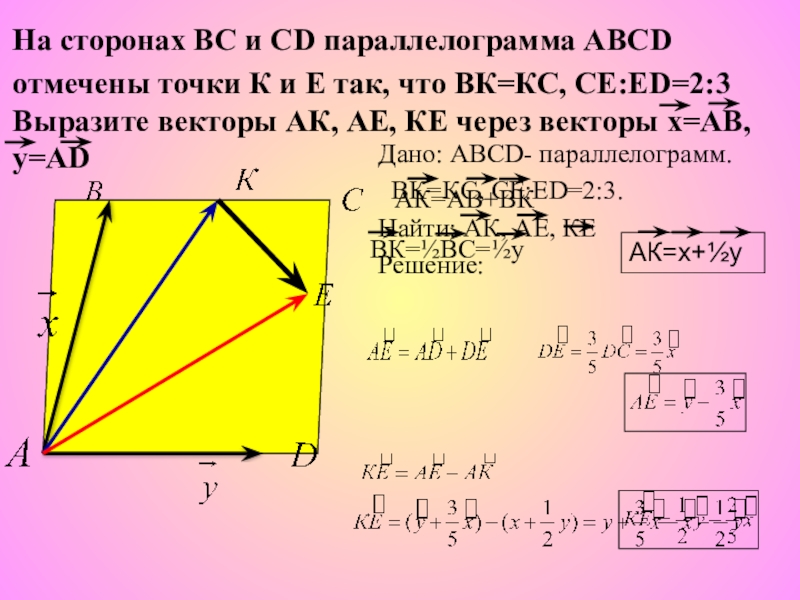
Слайд 9Дано: ABCD- параллелограмм.
BК=КC, СЕ:ЕD=2:3.
Найти: АК, АЕ, КЕ
Решение:
На сторонах ВС
отмечены точки К и Е так, что ВК=КС, СЕ:ЕD=2:3 Выразите векторы АК, АЕ, КЕ через векторы х=АВ, у=AD
АК=АВ+ВК
ВК=½ВС=½у
АК=х+½у