- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Разные задачи на многогранники, цилиндр, конус и шар
Содержание
- 1. Разные задачи на многогранники, цилиндр, конус и шар
- 2. Слайд 2
- 3. Слайд 3
- 4. Какая призма называется вписанной в сферу?
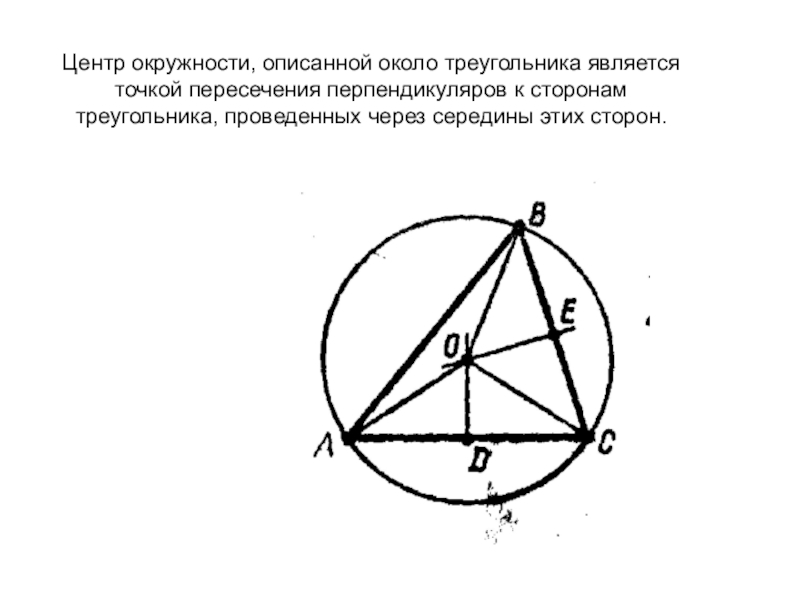
- 5. Центр окружности, описанной около треугольника является точкой
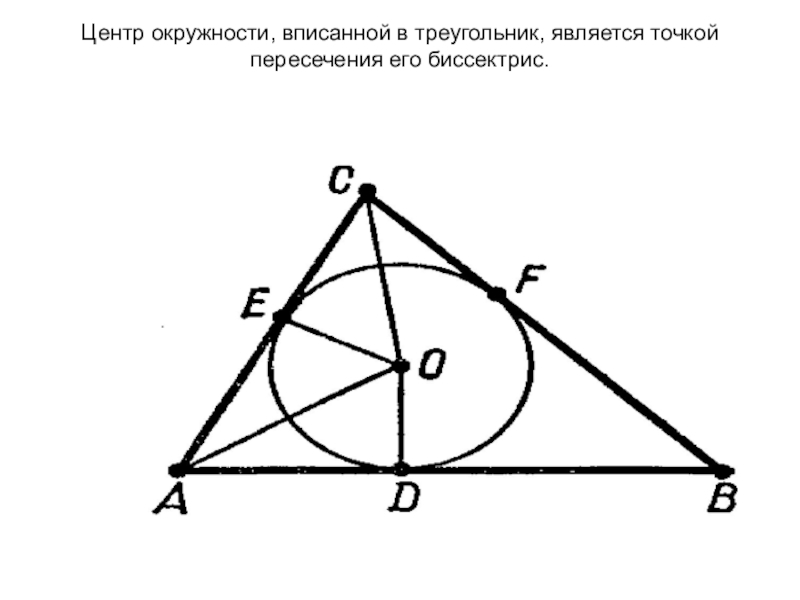
- 6. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
- 7. Шар вписанный в пирамиду. В любую треугольную
- 8. Слайд 8
- 9. Описанный шар около пирамиды. Около любой пирамиды
- 10. Слайд 10
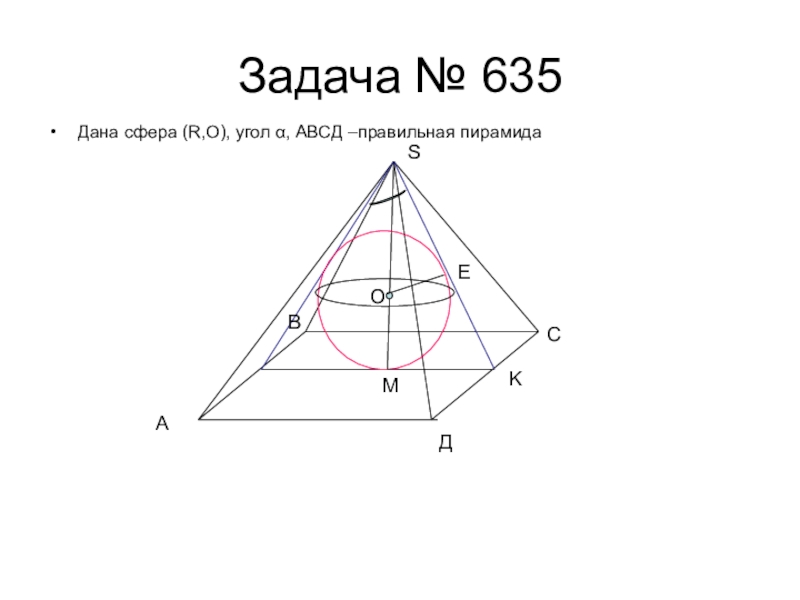
- 11. Задача № 635Дана сфера (R,O), угол α, АВСД –правильная пирамидаАВСДSEKMO
- 12. Шар, вписанный в призму Шар можно вписать
- 13. Слайд 13
- 14. Шар, описанный около призмы. Около призмы можно
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
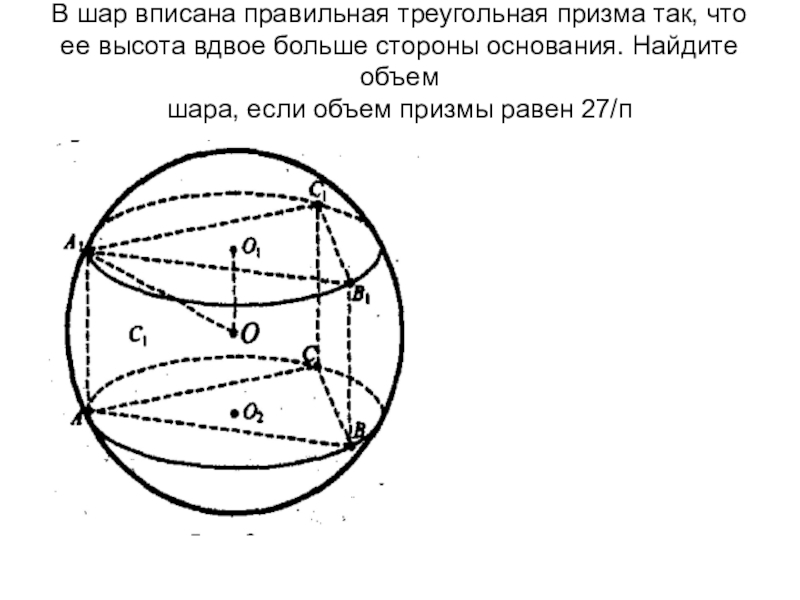
- 20. В шар вписана правильная треугольная призма так,
Какая призма называется вписанной в сферу? Какая призма называется описанной около сферы? Какая призма называется правильной? Около всякого ли прямоугольника можно описать окружность? Где находится центр этой окружности? Во всякий ли прямоугольник можно вписать окружность?
Слайд 4 Какая призма называется вписанной в сферу?
Какая призма называется описанной
около сферы?
Какая призма называется правильной?
Около всякого ли прямоугольника можно описать окружность?
Где находится центр этой окружности?
Во всякий ли прямоугольник можно вписать окружность?
А в какой можно?
Какая призма называется правильной?
Около всякого ли прямоугольника можно описать окружность?
Где находится центр этой окружности?
Во всякий ли прямоугольник можно вписать окружность?
А в какой можно?
Слайд 5Центр окружности, описанной около треугольника является точкой пересечения перпендикуляров к сторонам
треугольника, проведенных через середины этих сторон.
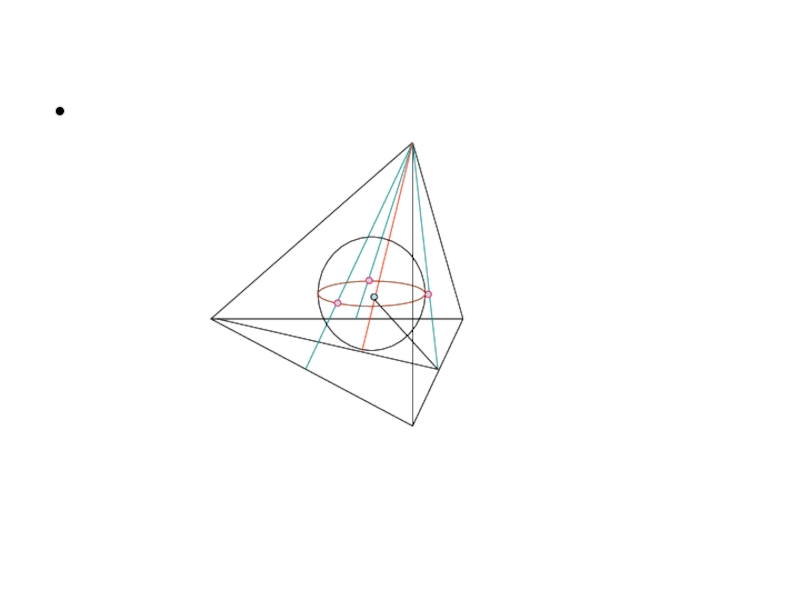
Слайд 7Шар вписанный в пирамиду.
В любую треугольную пирамиду можно вписать шар
В пирамиду,
у которой в основание можно вписать окружность, центр которой служит основанием высоты пирамиды, можно вписать шар.
В любую правильную пирамиду можно вписать шар.
Центр шара, вписанного в пирамиду, есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и ее проекцией на основание.
Центр шара, вписанного в правильную пирамиду, лежит на высоте этой пирамиды.
В любую правильную пирамиду можно вписать шар.
Центр шара, вписанного в пирамиду, есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и ее проекцией на основание.
Центр шара, вписанного в правильную пирамиду, лежит на высоте этой пирамиды.
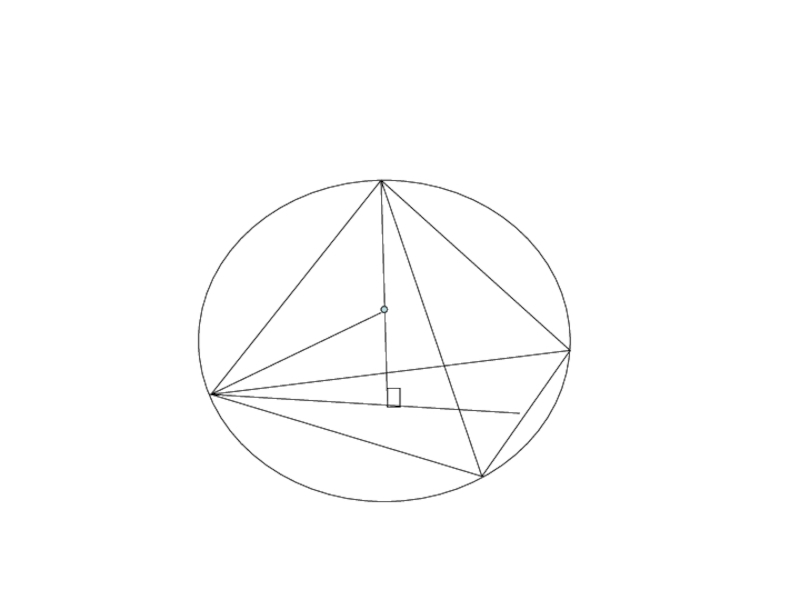
Слайд 9Описанный шар около пирамиды.
Около любой пирамиды можно описать шар.
Если около основания
пирамиды можно описать окружность, то около пирамиды можно описать шар.
Около любой правильной пирамиды можно описать шар.
Центр шара, описанного около пирамиды, лежит в точке пересечения прямой перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.
Около любой правильной пирамиды можно описать шар.
Центр шара, описанного около пирамиды, лежит в точке пересечения прямой перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.
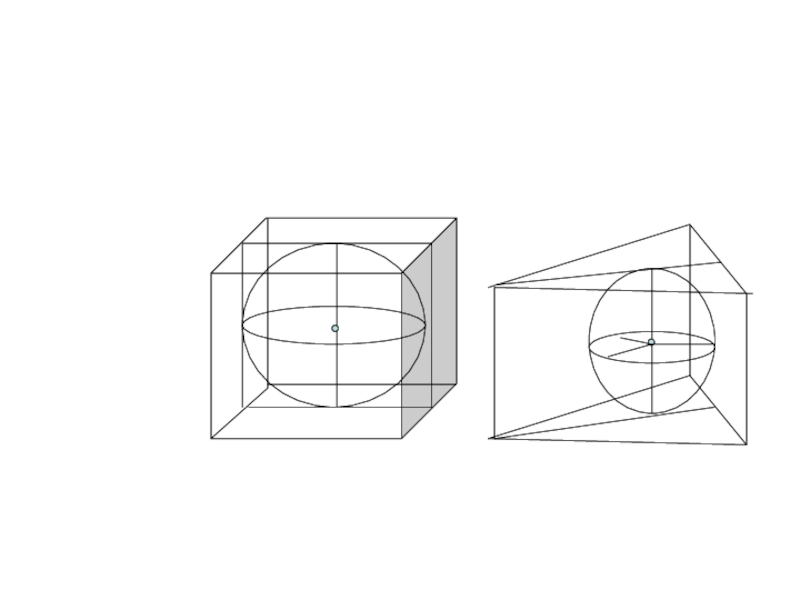
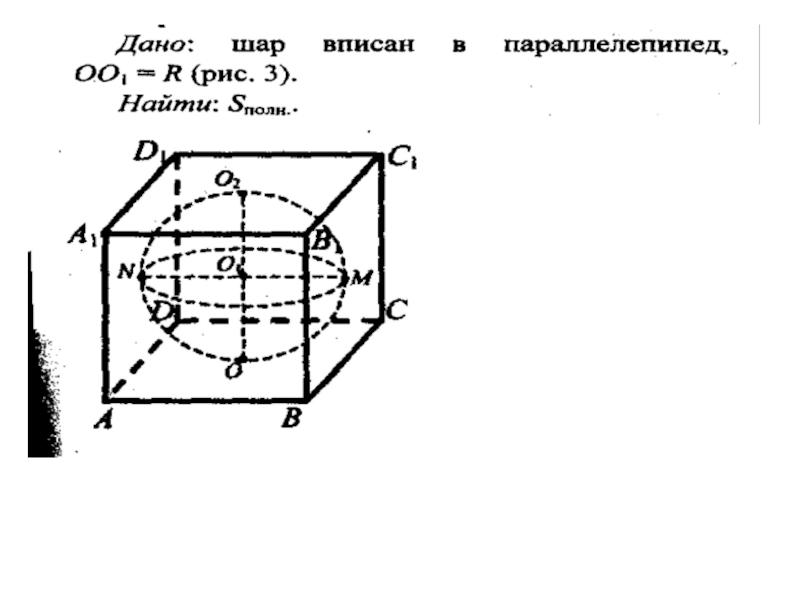
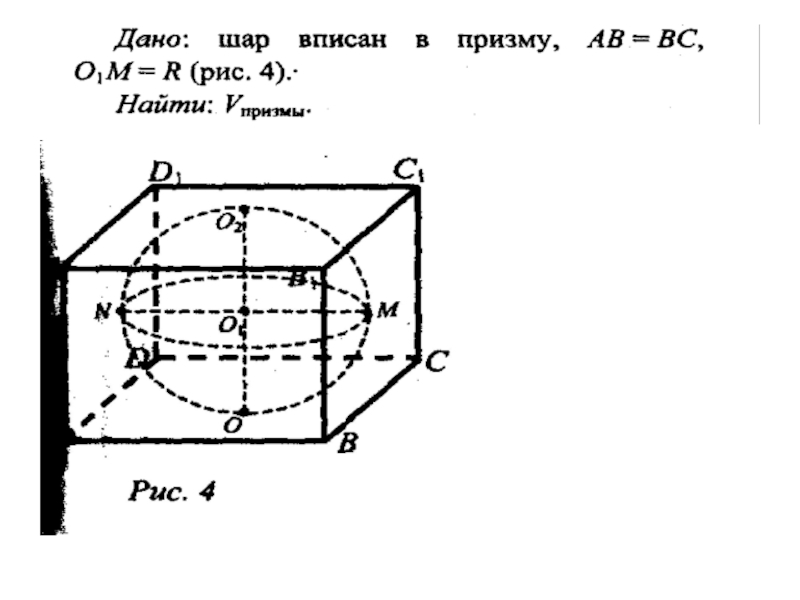
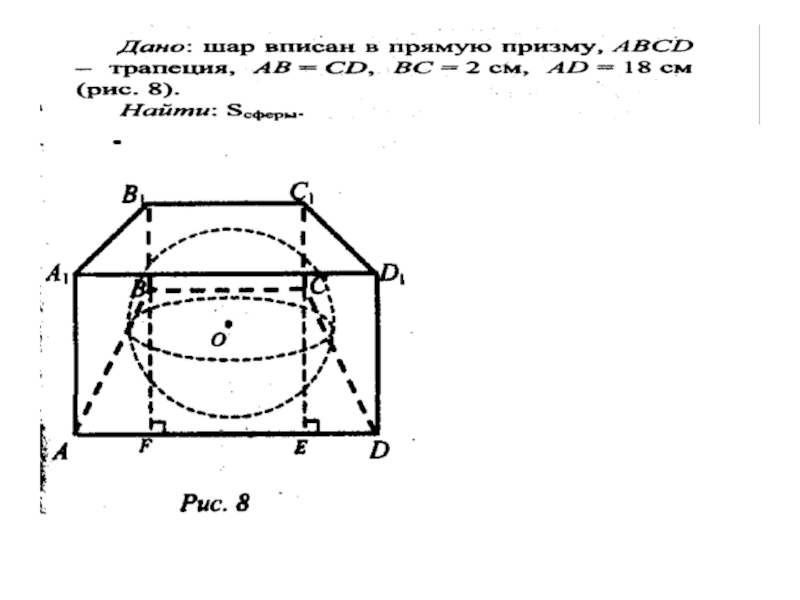
Слайд 12Шар, вписанный в призму
Шар можно вписать в прямую призму, если в
основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.
Центр вписанного шара лежит на середине высоты прямой призмы, проходящей через центры окружностей вписанных в основания призмы, а радиус шара равен радиусу окружности, вписанной в основание призмы.
Центр вписанного шара лежит на середине высоты прямой призмы, проходящей через центры окружностей вписанных в основания призмы, а радиус шара равен радиусу окружности, вписанной в основание призмы.
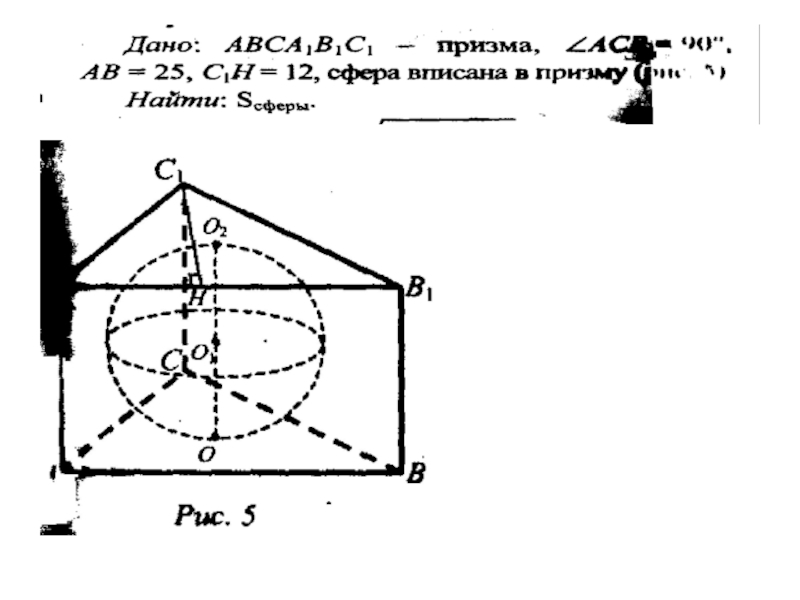
Слайд 14Шар, описанный около призмы.
Около призмы можно описать шар тогда и только
тогда, когда призма прямая и около основания можно описать окружность.
Центр шара, описанного около прямой призмы, лежит на середине высоты призмы, проведенной через центр окружности, описанной около основания.
Центр шара, описанного около прямой призмы, лежит на середине высоты призмы, проведенной через центр окружности, описанной около основания.
Слайд 20В шар вписана правильная треугольная призма так, что ее высота вдвое
больше стороны основания. Найдите объем
шара, если объем призмы равен 27/п