Д. Пойа
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Прямоугольный параллелепипед, 10 класс
Содержание
- 1. Прямоугольный параллелепипед, 10 класс
- 2. B10 № 245374. Найдите угол ABD многогранника, изображенного на
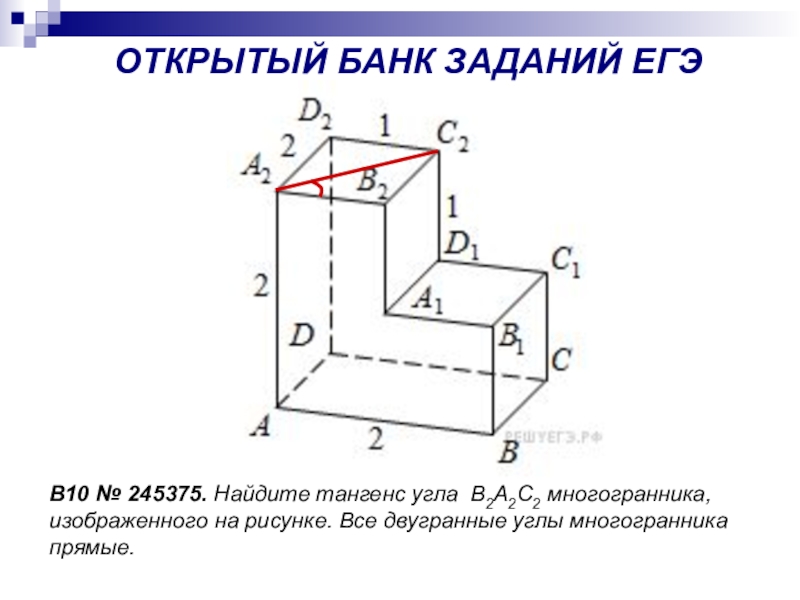
- 3. B10 № 245375. Найдите тангенс угла В2А2С2 многогранника, изображенного
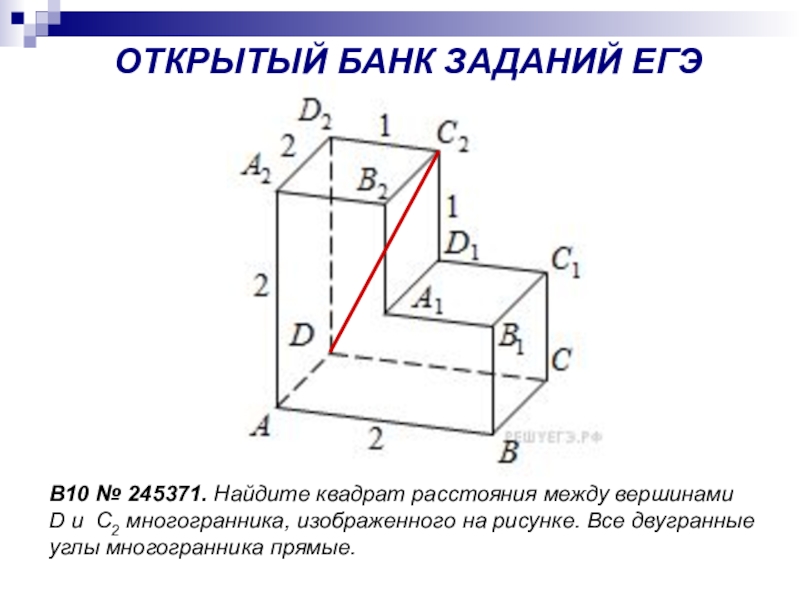
- 4. B10 № 245371. Найдите квадрат расстояния между вершинами
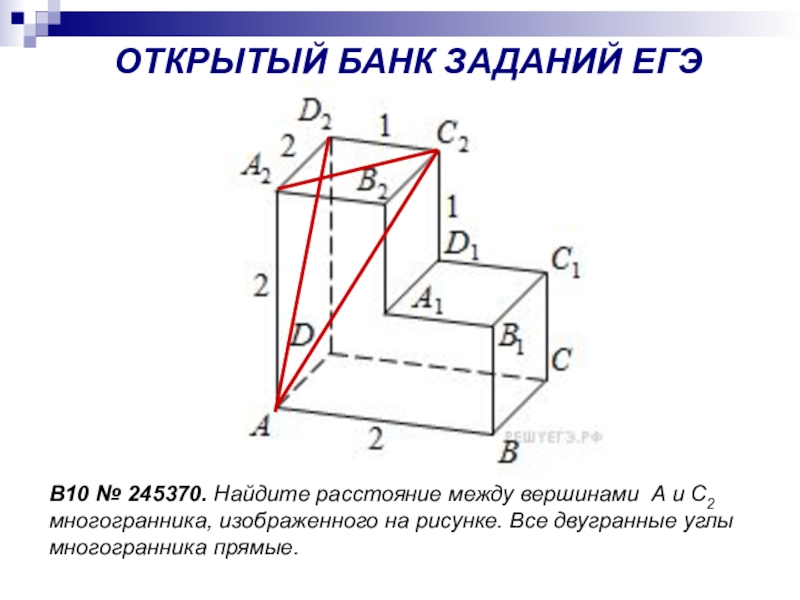
- 5. B10 № 245370. Найдите расстояние между вершинами А и
- 6. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД ТЕМА УРОКА:
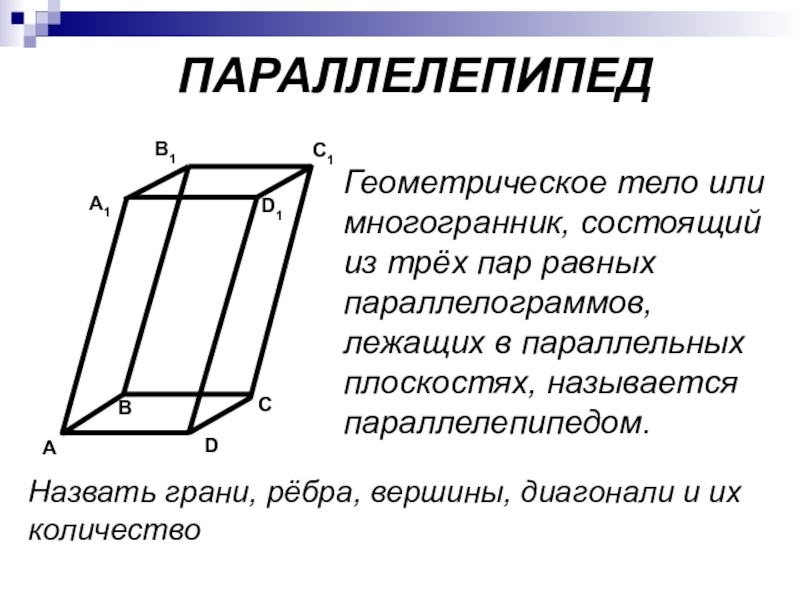
- 7. Геометрическое тело или многогранник, состоящий из трёх
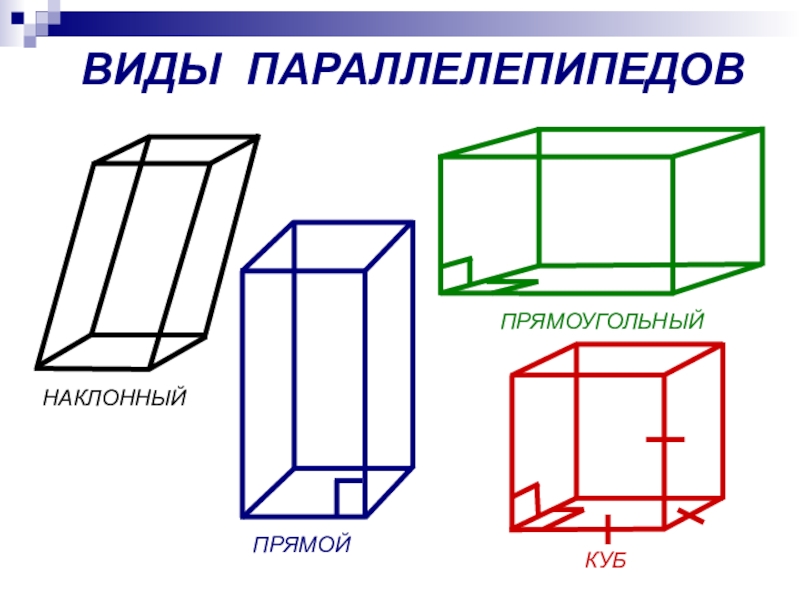
- 8. ВИДЫ ПАРАЛЛЕЛЕПИПЕДОВНАКЛОННЫЙПРЯМОЙПРЯМОУГОЛЬНЫЙКУБ
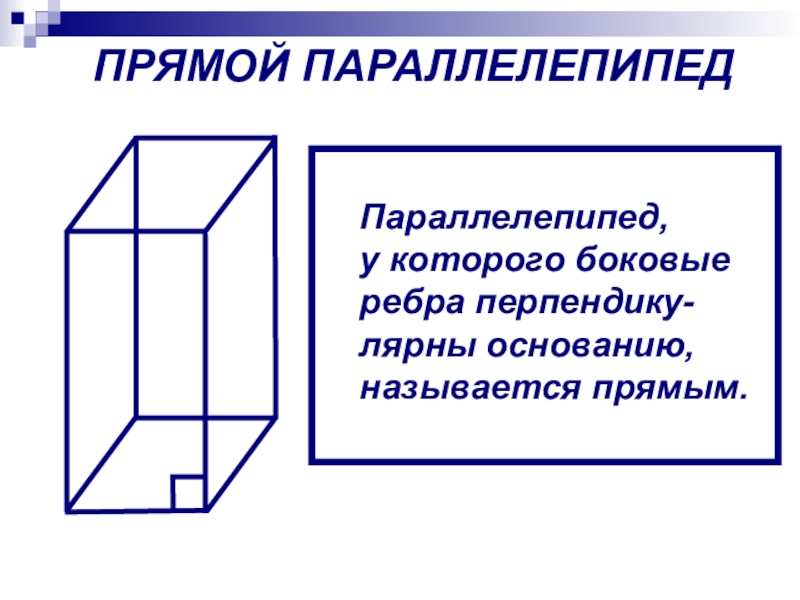
- 9. ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕДПараллелепипед, у которого боковые ребра перпендику-лярны основанию, называется прямым.
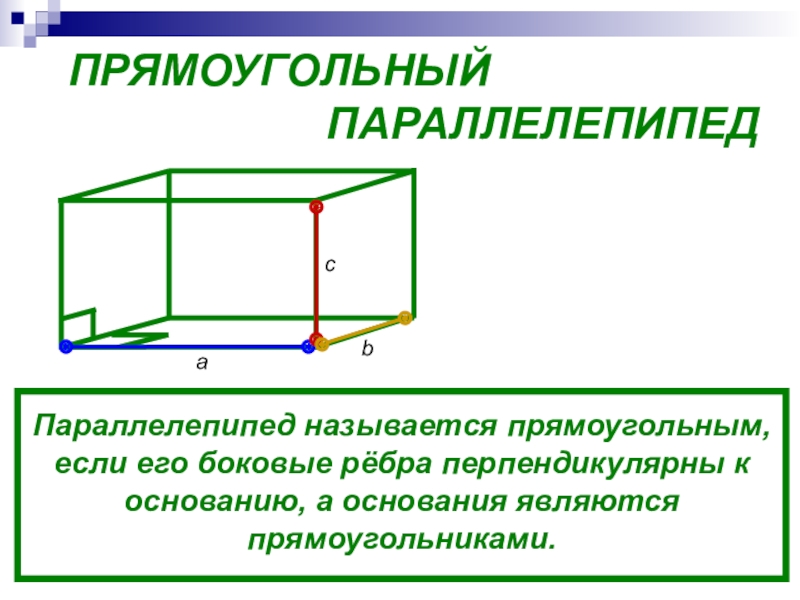
- 10. ПРЯМОУГОЛЬНЫЙ
- 11. ПРАВИЛЬНЫЙ
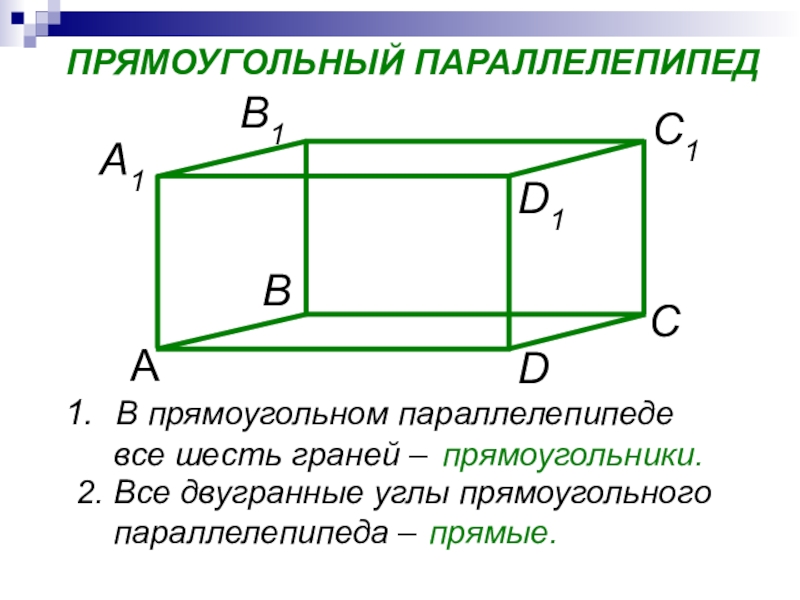
- 12. В прямоугольном параллелепипеде все
- 13. ПланиметрияСтереометрияВ прямоугольнике квадрат диагонали равен сумме квадратов
- 14. DА C1В СA1D1B1ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
- 15. Доказать: AC12=AB2+AD2+AA12Доказательство:2. Δ ABC – прямоугольный.По т.
- 16. B10 № 245370. Найдите расстояние между вершинами А и
- 17. № 189. Найдите расстояние от вершины куба
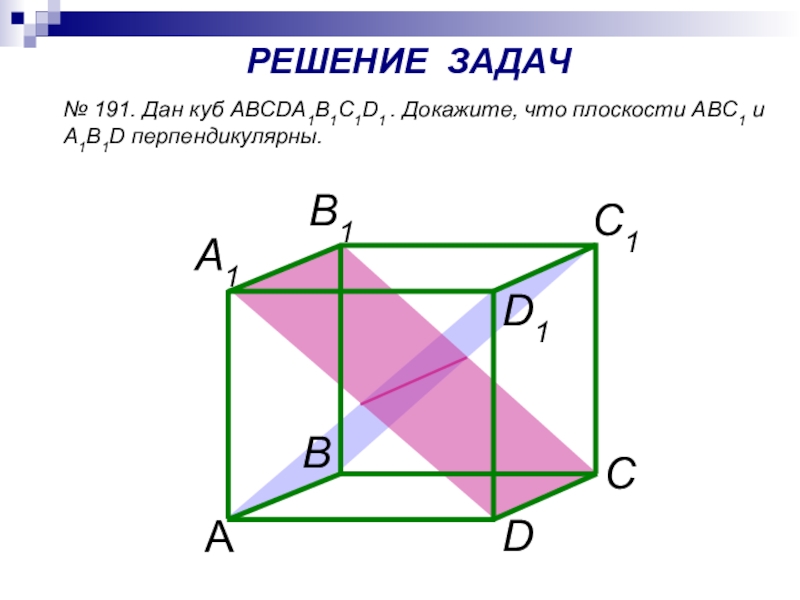
- 18. № 191. Дан куб ABCDA1B1C1D1 . Докажите, что плоскости ABC1 и A1B1D перпендикулярны.РЕШЕНИЕ ЗАДАЧ
- 19. ТЕСТВ прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что СС1=4,
B10 № 245374. Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.ОТКРЫТЫЙ БАНК ЗАДАНИЙ ЕГЭ
Слайд 2B10 № 245374. Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы
многогранника прямые. Ответ дайте в градусах.
ОТКРЫТЫЙ БАНК ЗАДАНИЙ ЕГЭ
Слайд 3B10 № 245375. Найдите тангенс угла В2А2С2 многогранника, изображенного на рисунке. Все двугранные
углы многогранника прямые.
ОТКРЫТЫЙ БАНК ЗАДАНИЙ ЕГЭ
Слайд 4B10 № 245371. Найдите квадрат расстояния между вершинами D и C2 многогранника,
изображенного на рисунке. Все двугранные углы многогранника прямые.
ОТКРЫТЫЙ БАНК ЗАДАНИЙ ЕГЭ
Слайд 5B10 № 245370. Найдите расстояние между вершинами А и С2 многогранника, изображенного на
рисунке. Все двугранные углы многогранника прямые.
ОТКРЫТЫЙ БАНК ЗАДАНИЙ ЕГЭ
Слайд 7Геометрическое тело или многогранник, состоящий из трёх пар равных параллелограммов, лежащих
в параллельных плоскостях, называется параллелепипедом.
Назвать грани, рёбра, вершины, диагонали и их количество
ПАРАЛЛЕЛЕПИПЕД
Слайд 9ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД
Параллелепипед,
у которого боковые
ребра перпендику-
лярны основанию,
называется прямым.
Слайд 10ПРЯМОУГОЛЬНЫЙ
ПАРАЛЛЕЛЕПИПЕД
Параллелепипед называется прямоугольным, если его боковые рёбра перпендикулярны к основанию, а основания являются прямоугольниками.
a
b
c
Слайд 12 В прямоугольном параллелепипеде
все шесть граней –
2.
Все двугранные углы прямоугольного
параллелепипеда –
параллелепипеда –
прямоугольники.
прямые.
D
А
C1
В
С
A1
D1
B1
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Слайд 13
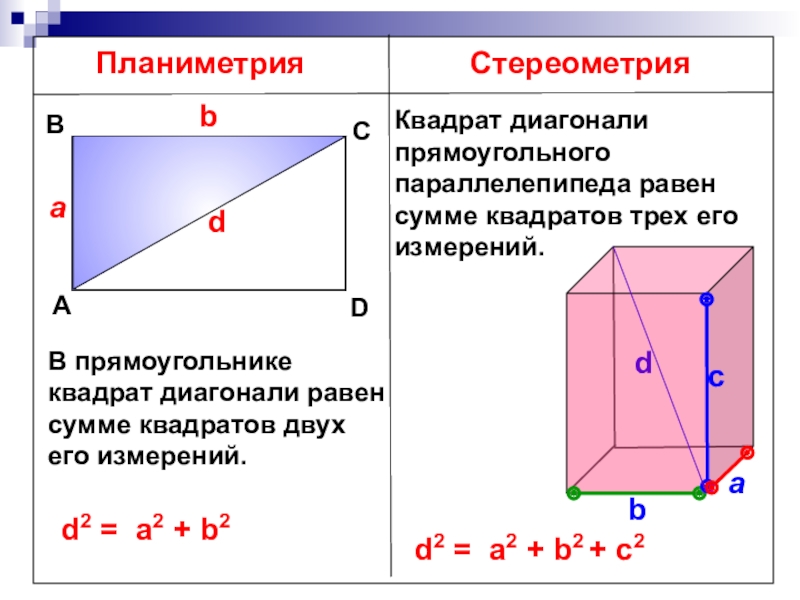
Планиметрия
Стереометрия
В прямоугольнике квадрат диагонали равен сумме квадратов двух его измерений.
А
В
С
D
d
a
b
d2 =
a2 + b2
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
d2 = a2 + b2 + с2
Слайд 14D
А
C1
В
С
A1
D1
B1
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов
трех его измерений.
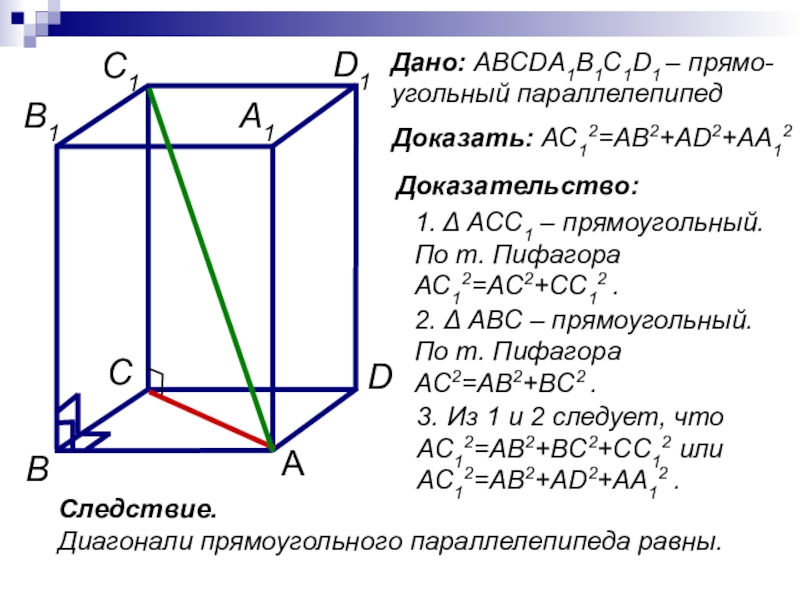
Слайд 15Доказать: AC12=AB2+AD2+AA12
Доказательство:
2. Δ ABC – прямоугольный.
По т. Пифагора
AC2=AB2+BC2 .
1. Δ ACC1
– прямоугольный.
По т. Пифагора
AC12=AC2+CC12 .
По т. Пифагора
AC12=AC2+CC12 .
3. Из 1 и 2 следует, что AC12=AB2+BC2+CC12 или AC12=AB2+AD2+AA12 .
Дано: ABCDA1B1C1D1 – прямо-угольный параллелепипед
Следствие.
Диагонали прямоугольного параллелепипеда равны.
Слайд 16B10 № 245370. Найдите расстояние между вершинами А и С2 многогранника, изображенного на
рисунке. Все двугранные углы многогранника прямые.
ОТКРЫТЫЙ БАНК ЗАДАНИЙ ЕГЭ
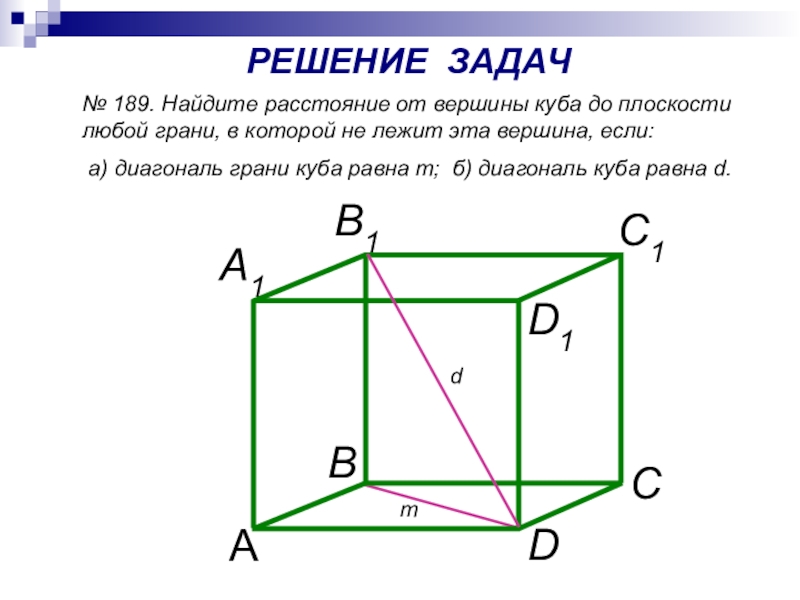
Слайд 17№ 189. Найдите расстояние от вершины куба до плоскости любой грани,
в которой не лежит эта вершина, если:
а) диагональ грани куба равна т; б) диагональ куба равна d.
а) диагональ грани куба равна т; б) диагональ куба равна d.
т
d
РЕШЕНИЕ ЗАДАЧ
Слайд 18
№ 191. Дан куб ABCDA1B1C1D1 . Докажите, что плоскости ABC1 и
A1B1D перпендикулярны.
РЕШЕНИЕ ЗАДАЧ
Слайд 19ТЕСТ
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что СС1=4, АВ=1, В1С1=8. Найти длину
диагонали DB1.
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1=5, CC1=3, В1С1=√7 . Найти длину ребра АВ.
Найдите квадрат расстояния между вершинами A3 и C многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Ответ: 9
Ответ: 3
Ответ: 17
