МКОУ ООШ п. Пудожгорский
Гостева С.А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Прямоугольник. Ромб. Квадрат
Содержание
- 1. Прямоугольник. Ромб. Квадрат
- 2. Цель урока:создать условия для развития умений решать
- 3. Задачи урока:создать условия для:закрепления знаний, умения и
- 4. Повторение.1) Продолжи определения:Четырехугольник, у которого противоположные стороны
- 5. Устная работа.Какая фигура называется многоугольником?Какой многоугольник называется
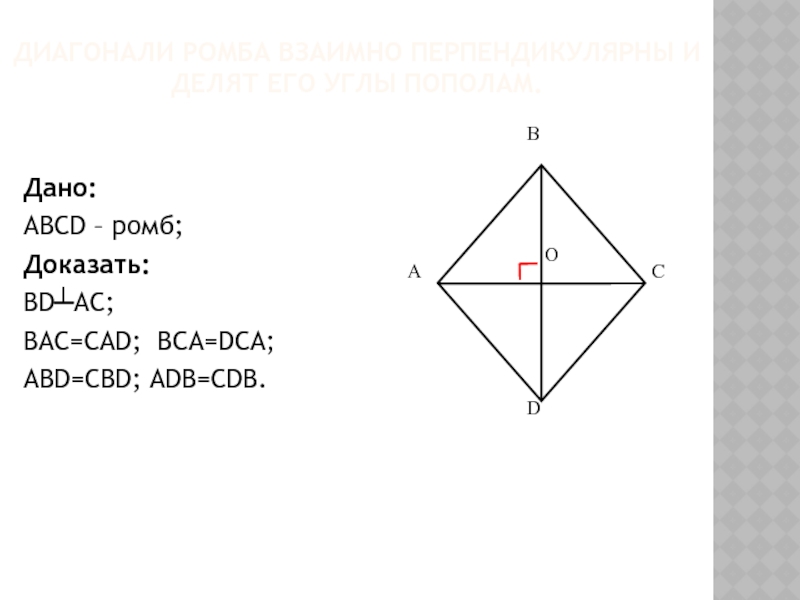
- 6. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.Дано:АВСD – ромб;Доказать:ВD┴АС;ВАС=САD; ВСА=DСА;АВD=СВD; АDВ=СDВ.
- 7. Доказательство:AB=AD (по определению ромба).ΔАВС=ΔАDC (по трем сторонам)
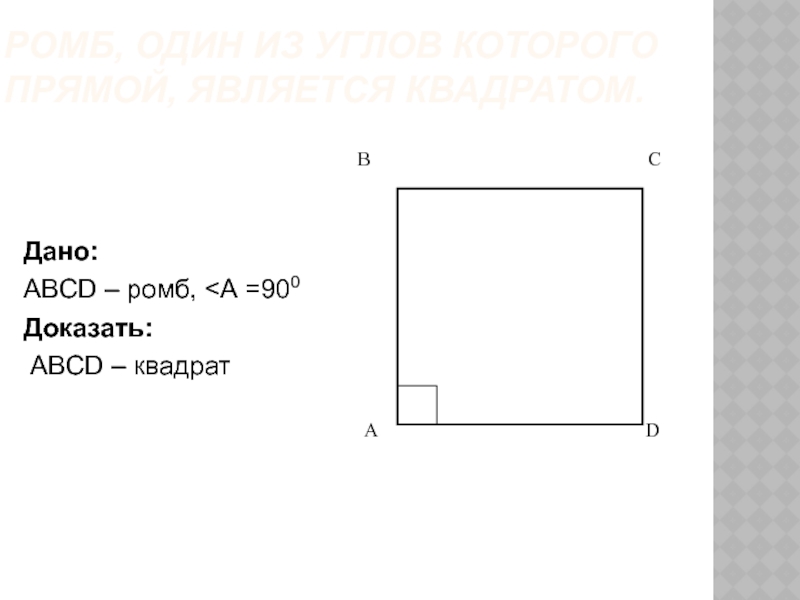
- 8. ромб, один из углов которого прямой, является квадратом.Дано: ABCD – ромб,
- 9. Доказательство:ABCD – ромб по условию, следовательно, AB=BC=CD
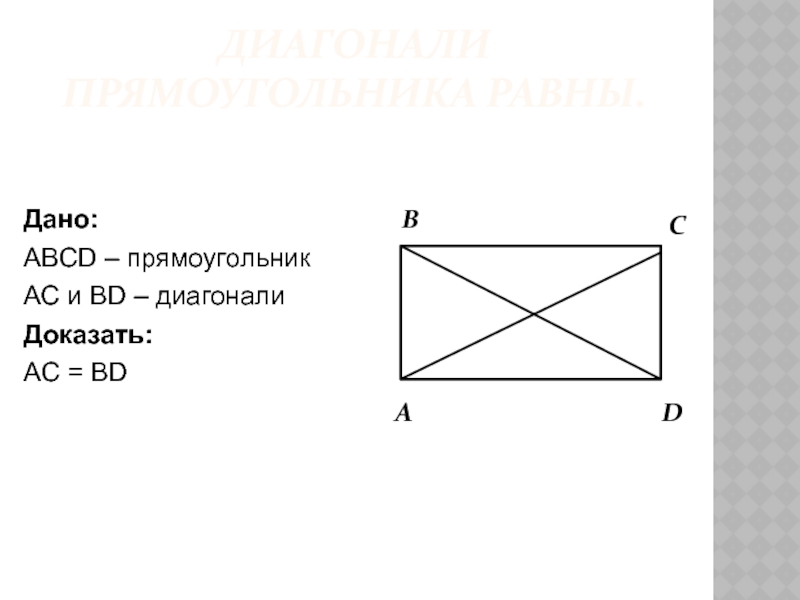
- 10. Диагонали прямоугольника равны.Дано:ABCD – прямоугольникАС и BD – диагоналиДоказать: AC = ВD
- 11. Доказательство:Рассмотрим прямоугольник ABCD.∆ABD, ∆ACD – прямоугольные.∆ABD =
- 12. Решение задач. Устно. Дано: АВСD – ромб,
- 13. Квадрат.Это прямоугольник, у которого все стороны равны.Это
- 14. ромбэто параллелограмм, у которого все стороны равны.Свойства
- 15. Прямоугольник.это четырехугольник у которого две противоположные стороны
- 16. Урок геометрии – это, во-первых, знание теории
Цель урока:создать условия для развития умений решать задачи по теме «Прямоугольник. Ромб. Квадрат», применяя изученные определения и свойства.
Слайд 2Цель урока:
создать условия для развития умений решать задачи по теме «Прямоугольник.
Ромб. Квадрат», применяя изученные определения и свойства.
Слайд 3Задачи урока:
создать условия для:
закрепления знаний, умения и навыков учащихся по теме
“ Прямоугольник. Ромб. Квадрат ”;
обобщения и систематизации теоретических знаний учащихся по теме “ Прямоугольник. Ромб. Квадрат ”;
развивать внимание, память, логическое мышление; активизировать мыслительную деятельность, умение анализировать, обобщать и рассуждать;
воспитание трудолюбия, усердия в достижении цели, интерес к предмету.
обобщения и систематизации теоретических знаний учащихся по теме “ Прямоугольник. Ромб. Квадрат ”;
развивать внимание, память, логическое мышление; активизировать мыслительную деятельность, умение анализировать, обобщать и рассуждать;
воспитание трудолюбия, усердия в достижении цели, интерес к предмету.
Слайд 4Повторение.
1) Продолжи определения:
Четырехугольник, у которого противоположные стороны попарно параллельны называется…
Параллелограмм, у
которого все углы прямые называется…
Параллелограмм, у которого все стороны равны называется…
Прямоугольник, у которого все стороны равны называется…
Ромб, у которого все углы прямые называется…
2) Решите задачу:
Периметр ромба 16 см. Найдите сторону ромба.
Параллелограмм, у которого все стороны равны называется…
Прямоугольник, у которого все стороны равны называется…
Ромб, у которого все углы прямые называется…
2) Решите задачу:
Периметр ромба 16 см. Найдите сторону ромба.
Слайд 5Устная работа.
Какая фигура называется многоугольником?
Какой многоугольник называется выпуклым?
Чему равна сумма углов
выпуклого четырехугольника?
Дайте определение параллелограмма? Является ли параллелограмм выпуклым четырехугольником?
Сформулируйте свойства параллелограмма.
Сформулируйте признаки параллелограмма.
Какой четырехугольник называется прямоугольником?
Какими свойствами обладает прямоугольник?
Сформулируйте особое свойство прямоугольника.
Сформулируйте признак прямоугольника.
Сформулируйте особое свойство ромба.
Какой четырехугольник называется ромбом? Какими свойствами обладает ромб?
Дайте определение параллелограмма? Является ли параллелограмм выпуклым четырехугольником?
Сформулируйте свойства параллелограмма.
Сформулируйте признаки параллелограмма.
Какой четырехугольник называется прямоугольником?
Какими свойствами обладает прямоугольник?
Сформулируйте особое свойство прямоугольника.
Сформулируйте признак прямоугольника.
Сформулируйте особое свойство ромба.
Какой четырехугольник называется ромбом? Какими свойствами обладает ромб?
Слайд 6Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Дано:
АВСD – ромб;
Доказать:
ВD┴АС;
ВАС=САD;
ВСА=DСА;
АВD=СВD; АDВ=СDВ.
АВD=СВD; АDВ=СDВ.
Слайд 7Доказательство:
AB=AD (по определению ромба).
ΔАВС=ΔАDC (по трем сторонам) ВАС=САD; ВСА=DСА;
ΔАВD=ΔСВD (по трем
сторонам) АВD=СВD; АDВ=СDВ.
ΔАВС – равнобедренный.
AO=OC (свойство параллелограмма). Следовательно ВО – медиана к стороне АС (т.к.диагонали ромба точкой пересечения делятся пополам).
ВО – высота ВD┴АС.
ΔАВС – равнобедренный.
AO=OC (свойство параллелограмма). Следовательно ВО – медиана к стороне АС (т.к.диагонали ромба точкой пересечения делятся пополам).
ВО – высота ВD┴АС.
Слайд 8ромб, один из углов которого прямой, является квадратом.
Дано:
ABCD – ромб,
<А =900
Доказать:
ABCD – квадрат
Доказать:
ABCD – квадрат
Слайд 9Доказательство:
ABCD – ромб по условию, следовательно, AB=BC=CD =AD, < А =
< В, < В = < D.
<А =900 по условию, < А = < С, следовательно < С = 900.
< А + < В = 1800, < В = 1800 – 900 = 900.
< В = 900, < В = < D, следовательно < D = 900.
Все стороны равны и все углы равны , следовательно ABCD – квадрат.
<А =900 по условию, < А = < С, следовательно < С = 900.
< А + < В = 1800, < В = 1800 – 900 = 900.
< В = 900, < В = < D, следовательно < D = 900.
Все стороны равны и все углы равны , следовательно ABCD – квадрат.
Слайд 10Диагонали прямоугольника равны.
Дано:
ABCD – прямоугольник
АС и BD – диагонали
Доказать:
AC =
ВD
Слайд 11Доказательство:
Рассмотрим прямоугольник ABCD.
∆ABD, ∆ACD – прямоугольные.
∆ABD = ∆ACD по двум катетам
. (ВА=СD, AD – общий катет).
Следовательно, АС=BD.
Следовательно, АС=BD.
Слайд 12Решение задач. Устно.
Дано: АВСD – ромб, А = 400. Найдите
ВDA.
Дано: АВСD – прямоугольник, AF - биссектриса ВА D. Определите вид треугольника АВF и его углы.
Дано: АВСD – прямоугольник, СА D =340. Найдите:
углы ΔАОВ;
углы между диагоналями. (см. рис. на доске).
Дано: АВСD – прямоугольник, AF - биссектриса ВА D. Определите вид треугольника АВF и его углы.
Дано: АВСD – прямоугольник, СА D =340. Найдите:
углы ΔАОВ;
углы между диагоналями. (см. рис. на доске).
Слайд 13Квадрат.
Это прямоугольник, у которого все стороны равны.
Это ромб, у которого все
углы прямые.
Свойства квадрата:
Все углы квадрата – прямые, все стороны квадрата – равны.
Диагонали квадрата равны и пересекаются под прямым углом.
Диагонали квадрата делят его углы пополам.
Свойства квадрата:
Все углы квадрата – прямые, все стороны квадрата – равны.
Диагонали квадрата равны и пересекаются под прямым углом.
Диагонали квадрата делят его углы пополам.
Слайд 14ромб
это параллелограмм, у которого все стороны равны.
Свойства ромба:
Поскольку ромб – это
параллелограмм, то все свойства параллелограмма верны для ромба.
Диагонали ромба перпендикулярны.
Диагонали ромба являются биссектрисами его углов.
Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Диагонали ромба перпендикулярны.
Диагонали ромба являются биссектрисами его углов.
Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Слайд 15Прямоугольник.
это четырехугольник у которого две противоположные стороны равны и все четыре
угла одинаковы.
Свойства прямоугольника:
Противоположные стороны прямоугольника имеют одинаковую длину.
Противоположные стороны прямоугольника параллельны.
Прилегающие стороны прямоугольника всегда перпендикулярны.
Все четыре угла прямоугольника прямые.
Сумма углов прямоугольника равна 3600
Диагонали прямоугольника точкой пересечения делятся пополам.
Свойства прямоугольника:
Противоположные стороны прямоугольника имеют одинаковую длину.
Противоположные стороны прямоугольника параллельны.
Прилегающие стороны прямоугольника всегда перпендикулярны.
Все четыре угла прямоугольника прямые.
Сумма углов прямоугольника равна 3600
Диагонали прямоугольника точкой пересечения делятся пополам.
Слайд 16Урок геометрии – это, во-первых, знание теории и, во – вторых,
правильное и разумное применение этой теории на практике. Данный урок – это урок систематизации и обобщения полученных знаний и применение этих знаний на практике.