- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект на тему Четырехугольники
Содержание
- 1. Проект на тему Четырехугольники
- 2. СОДЕРЖАНИЕ Введение
- 3. ВВЕДЕНИЕ Цель моего проекта - исследовать
- 4. 1. Общее описание четырехугольников Определение:
- 5. 1.1. Виды четырехугольниковПараллелограммом называется четырехугольник, у которого
- 6. 2. Общие свойства четырехугольниковВсе четырехугольники имеют четыре
- 7. 2.1. Свойства и признаки параллелограммаСвойства: 1. В
- 8. 2.2. Свойство и признак прямоугольникаСвойство: Диагонали прямоугольника
- 9. 2.4. Свойства квадрата 1. Все углы квадрата
- 10. 3. Свойства произвольного четырёхугольника Полусумма двух противоположных
- 11. 4. Наличие свойств симметрии и признаки четырехугольников
- 12. ЗаключениеИзучив свойства и признаки четырёхугольников, я сделала
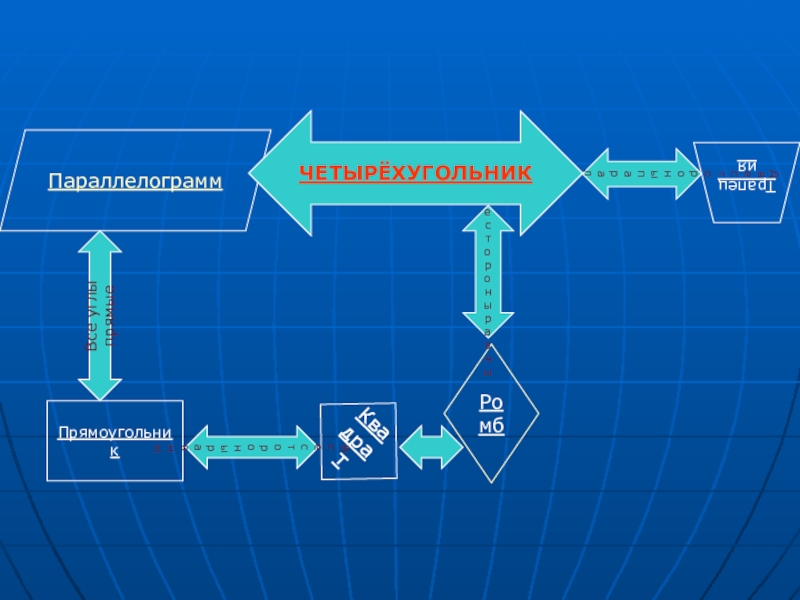
- 13. ПрямоугольникПараллелограммТрапецияРомбКвадрат Все стороны равныВсе стороны равныДве стороны параллельныВсе углы прямыеЧЕТЫРЁХУГОЛЬНИК
- 14. Приложение Свойства и признаки четырёхугольников используются
СОДЕРЖАНИЕ Введение 1. Общее описание четырёхугольников 1.1. Виды четырехугольников 2. Свойства четырехугольников 2.1 Свойства и признаки параллелограмма
Слайд 1МОУ «Нижнепенская средняя общеобразовательная школа»
Четырехугольники
Выполнила:
Ученик 8 класса
Анищенко Андрей
Руководитель:
Учитель математики
Грунева
З.В.
Слайд 2СОДЕРЖАНИЕ
Введение
1. Общее описание четырёхугольников
1.1. Виды четырехугольников
2. Свойства четырехугольников
2.1 Свойства и признаки параллелограмма
2.2 Свойства и признаки прямоугольника
2.3 Свойства ромба
2.4 Свойства квадрата
2.5 Свойства трапеции
3. Свойства произвольного четырёхугольника
4. Наличие свойств симметрии и признаки
четырехугольников
Заключение
Приложение
1.1. Виды четырехугольников
2. Свойства четырехугольников
2.1 Свойства и признаки параллелограмма
2.2 Свойства и признаки прямоугольника
2.3 Свойства ромба
2.4 Свойства квадрата
2.5 Свойства трапеции
3. Свойства произвольного четырёхугольника
4. Наличие свойств симметрии и признаки
четырехугольников
Заключение
Приложение
Слайд 3ВВЕДЕНИЕ
Цель моего проекта - исследовать и сравнить свойства четырёхугольников.
Для достижения поставленной цели я решаю следующие задачи:
изучить свойства сторон четырёхугольников,
изучить свойства углов четырёхугольников,
рассмотреть особые свойства четырёхугольников
Методы исследования: систематический сбор информации.
Объект исследования: геометрические фигуры-четырёхугольники.
Я считаю свою работу актуальной, потому что, изучая геометрию, многие могут не замечать сходства и различия свойств этих фигур.
Новизна моей работы в том, что ранее никто из учащихся не обращался к данной теме в своих исследованиях.
Слайд 41. Общее описание четырехугольников
Определение:
Четырёхугольник – это многоугольник ,
у которого четыре вершины и четыре стороны.
Четырёхугольник может быть выпуклым
(если он лежит по одну сторону от каждой
прямой, проходящей через две его соседние
вершины)
или невыпуклым (если он лежит по обе
стороны хотя бы от одной прямой,
проходящей через две его соседние
вершины)
Четырёхугольник может быть выпуклым
(если он лежит по одну сторону от каждой
прямой, проходящей через две его соседние
вершины)
или невыпуклым (если он лежит по обе
стороны хотя бы от одной прямой,
проходящей через две его соседние
вершины)
Слайд 51.1. Виды четырехугольников
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Трапецией
называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Ромбом называется параллелограмм, у которого все стороны равны.
Квадратом называется прямоугольник, у которого все стороны равны.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Ромбом называется параллелограмм, у которого все стороны равны.
Квадратом называется прямоугольник, у которого все стороны равны.
Слайд 62. Общие свойства четырехугольников
Все четырехугольники имеют четыре стороны
Все четырехугольники имеют четыре
угла
У всех четырехугольников есть 2 диагонали
Сумма углов выпуклого четырёхугольника равна
(n-2)∙180º= (4-2) ∙180º=360 º
Каждая диагональ выпуклого четырёхугольника разделяет его на два треугольника, а две диагонали на четыре треугольника
У всех четырехугольников есть 2 диагонали
Сумма углов выпуклого четырёхугольника равна
(n-2)∙180º= (4-2) ∙180º=360 º
Каждая диагональ выпуклого четырёхугольника разделяет его на два треугольника, а две диагонали на четыре треугольника
Слайд 72.1. Свойства и признаки параллелограмма
Свойства:
1. В параллелограмме противоположные стороны равны
и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Признаки:
1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам , то этот четырехугольник – параллелограмм.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Признаки:
1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам , то этот четырехугольник – параллелограмм.
Слайд 82.2. Свойство и признак прямоугольника
Свойство: Диагонали прямоугольника равны
Признак: Если в параллелограмме
диагонали равны, то этот параллелограмм – прямоугольник.
2.3. Свойство ромба
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
2.3. Свойство ромба
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Слайд 92.4. Свойства квадрата
1. Все углы квадрата прямые.
2. Диагонали квадрата равны,
взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
2.5. Свойства трапеции
1. У равнобедренной трапеции углы при основаниях равны.
2. У равнобедренной трапеции диагонали равны
3.Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.
2.5. Свойства трапеции
1. У равнобедренной трапеции углы при основаниях равны.
2. У равнобедренной трапеции диагонали равны
3.Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.
Слайд 103. Свойства произвольного четырёхугольника
Полусумма двух противоположных сторон выпуклого четырёхугольника не
меньше средней линии двух других сторон.
Отрезок, соединяющий середины диагоналей выпуклого четырёхугольника, делится точкой пересечения средних линий пополам.
Выпуклый четырёхугольник, диагонали которого являются средними линиями данного четырёхугольника, является параллелограммом (параллелограмм Вариньона)
Отрезок, соединяющий середины диагоналей выпуклого четырёхугольника, делится точкой пересечения средних линий пополам.
Выпуклый четырёхугольник, диагонали которого являются средними линиями данного четырёхугольника, является параллелограммом (параллелограмм Вариньона)
Слайд 114. Наличие свойств симметрии и признаки четырехугольников
если многоугольник имеет
центр симметрии, то каждая его вершина симметрична другой вершине, т.е. имеет четное число вершин,
если многоугольник имеет ось симметрии, то каждая его вершина не лежащая на оси, симметрична некоторой другой его вершине,
если четырехугольник имеет центр симметрии, то он параллелограмм,
если выпуклый четырехугольник имеет хотя бы одну ось симметрии, то он либо равнобокая трапеция, либо прямоугольник, либо дельтоид,
если выпуклый четырехугольник имеет две оси симметрии, то он либо ромб, либо прямоугольник,
если выпуклый четырехугольник имеет более двух осей симметрии, то он является квадратом и имеет четыре оси симметрии.
если многоугольник имеет ось симметрии, то каждая его вершина не лежащая на оси, симметрична некоторой другой его вершине,
если четырехугольник имеет центр симметрии, то он параллелограмм,
если выпуклый четырехугольник имеет хотя бы одну ось симметрии, то он либо равнобокая трапеция, либо прямоугольник, либо дельтоид,
если выпуклый четырехугольник имеет две оси симметрии, то он либо ромб, либо прямоугольник,
если выпуклый четырехугольник имеет более двух осей симметрии, то он является квадратом и имеет четыре оси симметрии.
Слайд 12Заключение
Изучив свойства и признаки четырёхугольников, я сделала вывод, что четырёхугольники взаимосвязаны
между собой свойствами: один вид четырёхугольника вытекает из другого вида посредством определённых свойств. Я отразила эту связь в следующей схеме:
Слайд 13Прямоугольник
Параллелограмм
Трапеция
Ромб
Квадрат
Все стороны равны
Все стороны равны
Две стороны
параллельны
Все углы прямые
ЧЕТЫРЁХУГОЛЬНИК
Слайд 14Приложение
Свойства и признаки четырёхугольников используются в задачах на:
нахождение величин
сторон, высот, диагоналей, углов;
нахождение площадей фигур и их частей;
нахождение пропорциональных отрезков;
нахождение отношения подобия;
нахождение величин элементов описанной и вписанной окружностей;
сравнение линейных величин и площадей фигур;
изучение свойств вписанных и описанных фигур.
нахождение площадей фигур и их частей;
нахождение пропорциональных отрезков;
нахождение отношения подобия;
нахождение величин элементов описанной и вписанной окружностей;
сравнение линейных величин и площадей фигур;
изучение свойств вписанных и описанных фигур.