- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект Геометрия у реки
Содержание
- 1. Проект Геометрия у реки
- 2. А знаете, многие ученики даже и
- 3. Природа говорит языком математики:буквы этого языка – круги, треугольникии иные математические фигуры.Галилей
- 4. Участники проекта - обучающиеся 8 класса Для решения поставленных задач 8 класс разделился на группы.
- 5. Геометрия у рекиПроект выполнили обучаюшиеся 7 класса:
- 6. Актуальность проекта Учебный проект рассматривает возможность применения
- 7. Гипотеза Можно ли воспользоваться приобретённымигеометрическими знаниями на
- 8. Цель проекта Применить полученные знания
- 9. Задачи исследования: С помощью геометрии выполнить задания:
- 10. Несколько дней мы ездили и ходили в походы для проведения исследований
- 11. И всегда нам мешал дождь И всегда нам мешал дождь
- 12. Измерение высоты дереваПрибрежная растительность рек Протвы
- 13. Измеряли высоту дерева при помощи простого булавочного прибора. Измерение высоты дерева
- 14. Измерение высоты дереваПриближаясь к дереву или
- 15. Измерение высоты дерева.Высота дерева 16,5 м
- 16. Измерение высоты дерева По другому способу
- 17. Измерение высоты дерева hдерева = 16,5 м
- 18. Измерение высоты дереваФото деревьевhдерева = 16,5 м
- 19. Измерение высоты дерева Самый лёгкий
- 20. Измерение высоты дерева
- 21. Измерение высоты дерева В один из
- 22. Измерение высоты дерева Вывод: применяя
- 23. Определение ширины рекиНе переплывая реки, измерить её
- 24. Определение ширины рекиВыбрав на противоположном берегу
- 25. Измерение высоты дерева.20м20м р. Протва10,5м
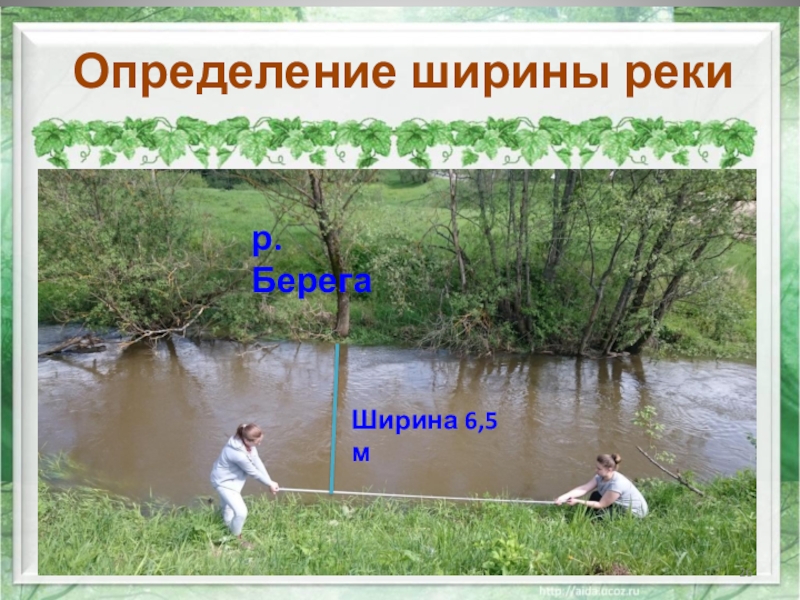
- 26. Определение ширины реки р. БерегаШирина 6,5м
- 27. Определение ширины реки ДCЕAВII способ можно
- 28. Определение ширины реки. 14
- 29. III способ:Определение ширины реки1. На другом берегу,
- 30. Определение ширины рекиШирина р.Береги в д.Бычково – 20,6мГлубина – 2,45м
- 31. Определение ширины рекиШирина р.Синица в д.Ивакино 1,5м
- 32. Определение ширины рекиВывод: представили три
- 33. Определение глубины рекиМы измеряли глубину реки с
- 34. Определение глубины рекир. Протва2,45м
- 35. Определение глубины рекир. Берега2,15м
- 36. Определение глубины реки Задача древних
- 37. Определение глубины реки
- 38. Определение глубины реки Растение возвышалось над водой
- 39. Определение глубины реки Вывод: с помощью двух
- 40. Определение крутизны склонаКрутизну склона, т. е. угол наклона
- 41. Определение крутизны склонаI cпособ: Для измерения крутизны
- 42. Определение крутизны склона Крутизна склона 170
- 43. Определение крутизны склона. Крутизна склона 200
- 44. Определение крутизны склонаII cпособ: Крутизна склона приближенно
- 45. Определение крутизны склона Крутизна склона 200
- 46. Определение скорости течения реки 20мВDАСДля измерения скорости
- 47. Определение скорости течения рекиНа линиях, перпендикулярных к
- 48. Определение скорости течения рекиТак вычислили скорость течения рек:
- 49. Круги на воде Вы не раз,
- 50. Круги на воде
- 51. Круги на воде На первый взгляд
- 52. Круги на воде
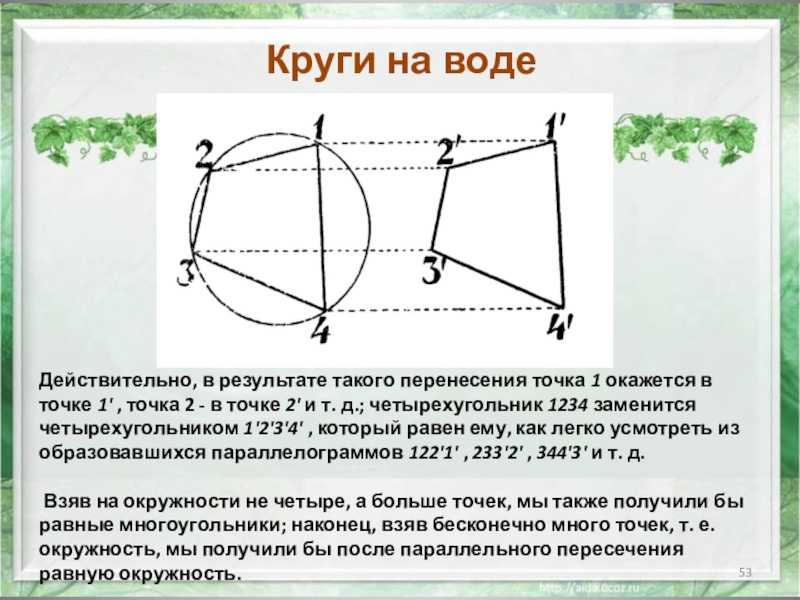
- 53. Круги на воде Действительно, в результате
- 54. Круги на воде Вот почему переносное
- 55. Геометрия листьев
- 56. Геометрия листьев Куда не глянь - всюду геометрия, геометрия даже в листьях.15см4смПоросль
- 57. Геометрия листьев 2 примерРассмотрим листья одуванчика.
- 58. Геометрия листьев 3,3см31см
- 59. Геометрия листьев Если, например, из двух
- 60. Заключение Яков Исидорович Перельман
- 61. ЗаключениеОгромную помощь в наших исследованиях оказала
- 62. Заключение Оказывается, все привлекательные стороны геометрии можно
- 63. Список литературы и интернет – ресурсов 1.
- 64.
Слайд 1
Презентацию подготовила учитель математики
Митрофанова Александра Федоровна
Mitrofanova Aleksandra Fedorovna
МОУ –
Можайский район, Московская область
Контактный телефон: 8 903 167 82 24
Адрес электронной почты: a.f.mitrofanova@mail.ru
Слайд 2
А знаете, многие ученики даже и не подозревали, как важна
Нам вместе удалось увидеть привлекательные стороны геометрии у реки.
Зная геометрию, можно измерить высоту дерева несколькими способами, не залезая на него; измерить скорость, ширину и глубину реки, находясь на берегу, измерить крутизну склона, увидеть геометрию в листьях деревьев, будут ли волны от камня, брошенного в воду быстрой реки иметь форму круга или же форма будет вытянутой в направлении тени.
Оказывается, зная геометрию, можно творить чудеса!!!
Слайд 3Природа говорит языком математики:
буквы этого языка – круги, треугольники
и иные математические
Галилей
Слайд 4Участники проекта - обучающиеся 8 класса
Для решения поставленных задач 8
Слайд 5Геометрия у реки
Проект выполнили обучаюшиеся 7 класса: ВоронинаН., Коровина А., Ермолаев
Проект называется
«Геометрия у реки»
Слайд 6Актуальность проекта
Учебный проект рассматривает возможность
применения учебных знаний в походе.
применять на практике основы геометрии.
Слайд 7Гипотеза
Можно ли воспользоваться приобретёнными
геометрическими знаниями на практике, например в походе?
р.
Можно ли воспользоваться приобретёнными
геометрическими знаниями на практике, например в походе?
Слайд 9Задачи исследования:
С помощью геометрии выполнить задания:
измерить высоту дерева;
измерить глубины рек;
определить крутизну склона;
определить скорость течения рек;
рассмотреть круги на воде;
геометрия листьев;
оформить результаты исследования в виде презентации.
Слайд 12
Измерение высоты дерева
Прибрежная растительность рек Протвы и Береги очень
По берегам рек растет много разных деревьев и кустарников.
Существует множество различных способов измерения высоты дерева, не срубая его и не взбираясь на верхушку, при помощи весьма незамысловатых приборов и даже без всяких приспособлений.
Слайд 14
Измерение высоты дерева
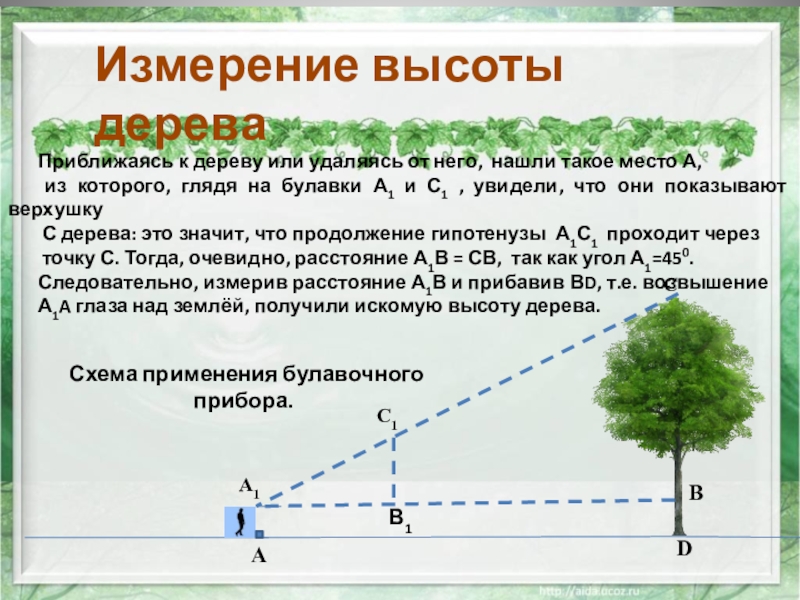
Приближаясь к дереву или удаляясь от него, нашли
из которого, глядя на булавки А1 и С1 , увидели, что они показывают верхушку
С дерева: это значит, что продолжение гипотенузы А1С1 проходит через
точку С. Тогда, очевидно, расстояние А1В = СВ, так как угол А1=450.
Следовательно, измерив расстояние А1В и прибавив ВD, т.е. возвышение
А1A глаза над землёй, получили искомую высоту дерева.
Схема применения булавочного прибора.
А1
С1
С
В1
В
А
D
Слайд 16 Измерение высоты дерева
По другому способу обошлись даже и без
высоте дерева.
А
С1
В1
С
В
Слайд 19
Измерение высоты дерева
Самый лёгкий и самый
Втыкаем вертикально шест в землю. Измеряем рулеткой длину шеста и его тени.
Обозначаем величину шеста за А1В1, а длину тени, которую он отбрасывает за В1С1. После этого измеряем величину тени от дерева AB, допустим это будет BC. Вычислим искомую высоту дерева АВ из пропорции: AB : А1В1 = BC : В1С1
Т.е. высота дерева во столько же раз больше высоты шеста, во сколько раз тень дерева длиннее тени шеста. Это вытекает, конечно, из геометрического подобия треугольников АВС и А1В1С1.
Надо только следить, чтобы шест стоял строго вертикально и не допускать погрешности в измерениях.
Слайд 21
Измерение высоты дерева
В один из солнечных
В качестве мерки взяли одноклассника. Его рост равен 1,68 м. Измерив, его тень мы получили результат – 3,6 м. Длина тени от дерева равнялась 39,9 м.
Из пропорции х : 1,68 = 39,9 : 3,6, получили высоту дерева 18,62м.
39,9 м
3,6 м
1,68 м
Слайд 22
Измерение высоты дерева
Вывод:
применяя различные способы
Слайд 23Определение ширины реки
Не переплывая реки, измерить её ширину – так же
I способ:
Ширина реки достаточно точно может быть определена способом построения на берегу реки двух равных прямоугольных треугольников.
Слайд 24
Определение ширины реки
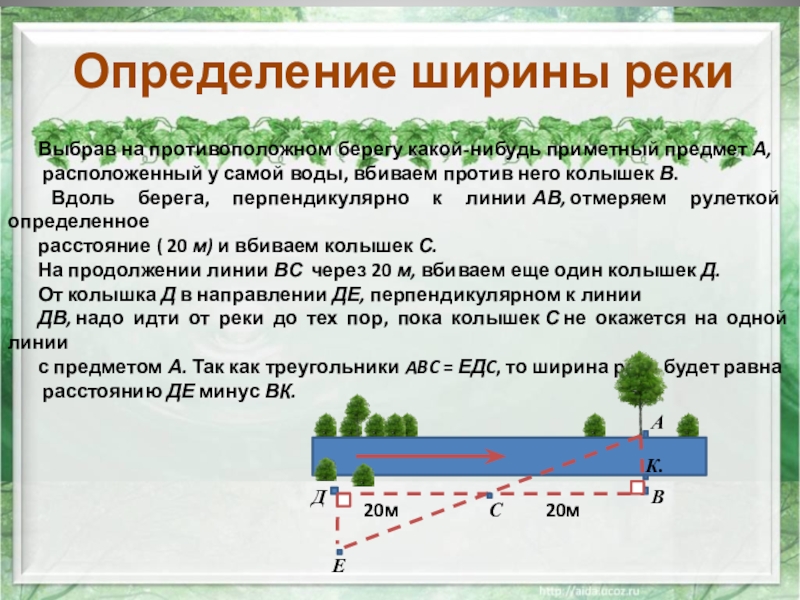
Выбрав на противоположном берегу какой-нибудь приметный предмет А,
расположенный
Вдоль берега, перпендикулярно к линии АВ, отмеряем рулеткой определенное
расстояние ( 20 м) и вбиваем колышек С.
На продолжении линии ВС через 20 м, вбиваем еще один колышек Д.
От колышка Д в направлении ДЕ, перпендикулярном к линии
ДВ, надо идти от реки до тех пор, пока колышек С не окажется на одной линии
с предметом А. Так как треугольники ABC = ЕДC, то ширина реки будет равна
расстоянию ДЕ минус ВК.
Д
C
Е
A
В
К.
20м
20м
Слайд 27
Определение ширины реки
Д
C
Е
A
В
II способ можно видоизменить: отмерить на
Мы взяли DC в четыре раза меньше BС, а далее поступают как в I способе: по направлению DE, перпендикулярному к DB, отыскивают точку E, из которой веха C кажется покрывающей точку А. Но теперь уже DE не равно АB, а меньше этого расстояния в четыре раза: треугольники ABC и ЕDC здесь не равны, а подобны. Из подобия треугольников следует пропорция АB : DE = ВС : СД = 4 : 1. Значит, измерив DE и умножив результат на 4, получим расстояние АВ, а отняв KВ, узнаем искомую ширину реки. Этот способ требует меньше места и потому удобнее для выполнения, чем предыдущий.
К
4
1
Слайд 29III способ:
Определение ширины реки
1. На другом берегу, у самого русла, мы
Слайд 32
Определение ширины реки
Вывод: представили три легко выполнимых приёма, при
Слайд 33Определение глубины реки
Мы измеряли глубину реки с берега с помощью удочки.
Слайд 36Определение глубины реки
Задача древних индусов
Над озером тихим,
С
Он рос одиноко.
И ветер порывом отнёс его в сторону.
Нет боле цветка над водой,
Нашёл же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?
Нашли еще один способ измерения глубины реки.
У древних индусов был обычай задачи и правила предлагать в стихах. Вот одна из таких задач:
Слайд 38Определение глубины реки
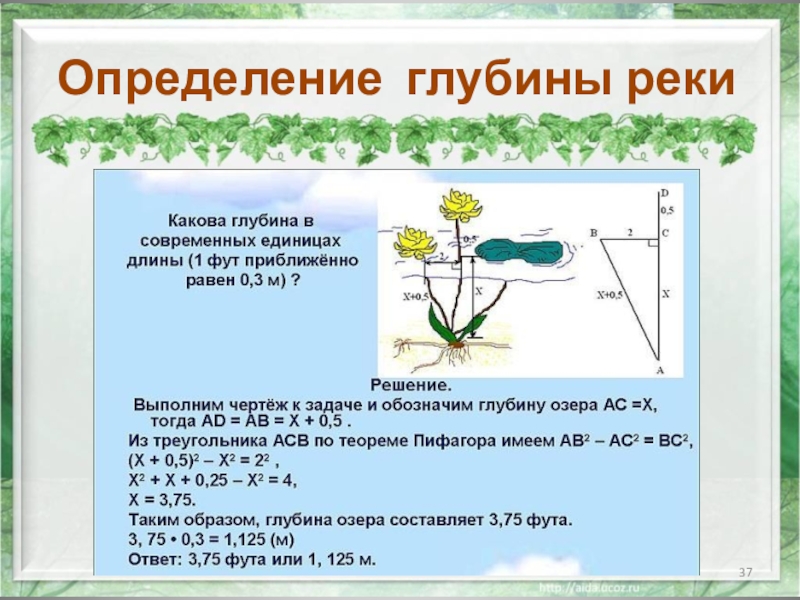
Растение возвышалось над водой на 0,5м. Перегнули
Рассмотрим прямоугольный треугольник BDС. Обозначим искомую глубину реки СD через х. Тогда, по теореме Пифагора, имеем:
BD² =DС2+СВ2, значит BD² =х2+СВ2
ВD= х+ 0,5, расстояние СВ=1,5м, получим
(х+ 0,5)2=х2 + 1,52,
х2+х+0,25=х2+2,25, отсюда х=2
Ответ: искомая глубина реки составила 2м.
0,5
1,5
Х+0,5
х
Близ берега реки мы отыскали водное растение, которое
доставило нам реальный материал для практической задачи:
без всяких приспособлений, не замочив даже рук, определить
глубину водоёма в неглубоком месте.
Слайд 39Определение глубины реки
Вывод: с помощью двух способов измерили
Определили, что средняя глубина рек
Протвы ≈ 2,45 м,
Береги ≈ 2,15 м
Слайд 40Определение крутизны склона
Крутизну склона, т. е. угол наклона поверхности склона к горизонтальной плоскости,
Слайд 41Определение крутизны склона
I cпособ: Для измерения крутизны склона прибор должен занять
Слайд 44Определение крутизны склона
II cпособ: Крутизна склона приближенно может быть определена измерением
Формула для вычисления крутизны склона: α =60/n, где n - количество пар шагов.
Слайд 46Определение скорости течения реки
20м
В
D
А
С
Для измерения скорости реки, мы выбрали участок
Выбрали 20 метровый отрезок АВ, поставили два колышка.
Слайд 47Определение скорости течения реки
На линиях, перпендикулярных к АВ, ставят еще две
20м
В
D
А
С
Слайд 49 Круги на воде
Вы не раз, конечно, с любопытством рассматривали
Но как обстоит дело в воде текучей? Должны ли волны от камня, брошенного в воду быстрой реки, тоже иметь форму круга, или же форма их будет вытянутая?
Слайд 51 Круги на воде
На первый взгляд может показаться, что
В действительности, однако, это не так. Бросая камни в самую быструю речку, вы можете убедиться, что волны получаются строго круговые — совершенно такие же, как и в стоячей воде. Почему?
Будем рассуждать так. Если бы вода не текла, волны были бы круговые. Какое же изменение вносит течение? Оно увлекает каждую точку этой круговой волны в направлении, указанном стрелками, причем все точки переносятся по параллельным прямым с одинаковой скоростью, т. е. на одинаковые расстояния. А «параллельное перенесение» не изменяет формы фигуры.
Слайд 53 Круги на воде
Действительно, в результате такого перенесения точка 1 окажется в
Взяв на окружности не четыре, а больше точек, мы также получили бы равные многоугольники; наконец, взяв бесконечно много точек, т. е. окружность, мы получили бы после параллельного пересечения равную окружность.
Слайд 54 Круги на воде
Вот почему переносное движение воды не изменяет
Слайд 55 Геометрия листьев
Оба листа различные по величине, имеют все же одинаковую или почти одинаковую форму: другими словами – это фигуры, геометрически подобные. Площади таких фигур, мы знаем, относятся, как квадраты их линейных размеров. Значит, определив, во сколько раз один лист длиннее или шире другого, мы простым возведением этого числа в квадрат узнаем отношение их площадей. Пусть лист поросли имеет длину 15см, а лист с ветви дерева – только 4см; отношение линейных размеров , и, значит, один больше другого по площади в ,т.е. в 14 раз.
1 пример
Слайд 57 Геометрия листьев
2 пример
Рассмотрим листья одуванчика. У одуванчика, выросшего в
Мы решили сравнить их площади и задали себе вопрос: «Во сколько примерно раз площадь первого листа больше, чем площадь второго.
Для решения этой проблемы поступаем, как и в предыдущей задаче. Отношение площадей равно:
Значит, один лист больше другого по площади в 80-90 раз.
Слайд 59 Геометрия листьев
Если, например, из двух листьев, геометрически подобных по
один длиннее другого на 20%, то отношение их площадей равно
т.е. разница составляет 44%.
А при различии ширины в 40% один лист превышает другой по
площади в
Т.е. почти вдвое.
Слайд 61 Заключение
Огромную помощь в наших исследованиях оказала книга «Геометрия на вольном
Эта книга написана не столько для друзей математики, сколько для её недругов. Автор предназначает книгу для той категории читателей, которые относятся к геометрии без особого интереса и одушевления.
Слайд 62 Заключение
Оказывается, все привлекательные стороны геометрии можно увидеть на вольном воздухе
Геометрия возникла на основе практической деятельности, поэтому важно знать как при помощи геометрии измерить некоторые величины.
Проект показывает, что геометрия – это не просто школьный предмет, а наука, находящая применение в жизни.
Слайд 63
Список литературы и интернет – ресурсов
1. Г.И. Глейзер ,« История
2. Г.П.Бевз, И.Г.Владимирова ,«Геометрия 7-11класс»,1994г.
3. Л.И.Звавич, А.Р.Рязановский «Геометрия в таблицах 7-11 классы» Москва.
Издательский дом «Дрофа» ,1997г.
4. Б.Г.Зив, В.Н.Мейлер ,«Задачи по геометрии», Москва «Просвещение», 2000г.
maps.yandex.ru.
5. Я. И. Перельман «Геометрия на вольном воздухе», Москва, «Астрель», 2007г.
marshruty.ru›Places/Place.aspx…; Исток реки.
ru.wikipedia.org›wiki/; Википедия.