- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Применение вектора к решению задач.
Содержание
- 1. Применение вектора к решению задач.
- 2. №784(б)-проверка д/з. ABCDВыразить через и OМAМ= MD
- 3. №786 – проверка д/з. ABCB1А1С1
- 4. 1.Упростите:
- 5. 2.Найдите x:
- 6. 3. ABCDMВыразить через и M- середина CBAN:NB=2:3N
- 7. №787 DEFGO
- 8. Вопрос №18 Задача 1.Точка С – середина
- 9. Вопрос №18 Задача 2.Доказать, что прямая, проведенная
- 10. АBMCDNOΔOAD~ΔBOC(∠O-общий, ∠A=∠OBC-соотв. при AD||BC)M-середина BC,N-середина AD,
- 11. и коллинеарны, то O∈NM
- 12. №785-пользуясь задачей 1АBCD∙O
- 13. Желаю успехов!Домашнее задание: Вопрос: 18- с доказательством.№785, 790-пользуясь задачей 1 .
№784(б)-проверка д/з. ABCDВыразить через и OМAМ= MD
Слайд 8Вопрос №18 Задача 1.
Точка С – середина отрезка AB, а точка
O – произвольная точка плоскости.
Доказать, что:
А
B
∙O
C
+
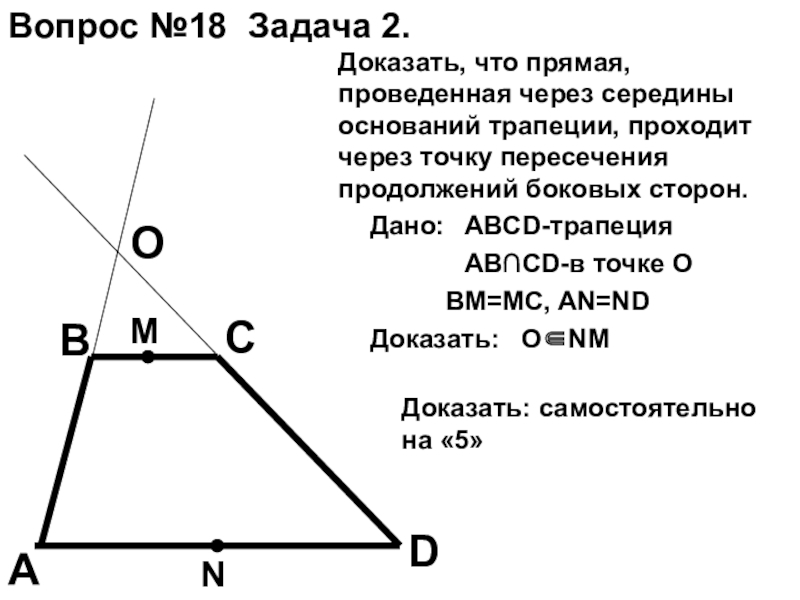
Слайд 9Вопрос №18 Задача 2.
Доказать, что прямая, проведенная через середины оснований трапеции,
проходит через точку пересечения продолжений боковых сторон.
А
B
M
C
D
Дано:
ABCD-трапеция
AB∩CD-в точке О
N
BM=MC, AN=ND
Доказать:
О∈NM
Доказать: самостоятельно на «5»
O