Анастасия
Учитель Бояхчян Наталья Евгеньевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Применение теоремы Пифагора.
Содержание
- 1. Применение теоремы Пифагора.
- 2. Теорема Пифагора:Сумма квадратов катетов равна квадрату гипотенузы.a²
- 3. Теорема применяется:в планиметриив стереометриив архитектурев строительствев физике
- 4. 1) В планиметрии:1. Квадрат со стороной а и диагональю d.
- 5. 2. Диагональ d прямоугольника со сторонами а
- 6. 3.Высота h равностороннего треугольника со стороной а может рассматриваться как катет
- 7. 2) В архитектуре: В зданиях готического и
- 8. Остается еще полная окружность, касающаяся четырех дуг.
- 9. В романской архитектуре часто встречается мотив, представленный
- 10. Собор Парижской Богоматери
- 11. 3) В строительстве: Если рассматривать треугольную призму
- 12. 4) В физике: Молниеотвод, громоотвод, устройство для защиты
- 13. 5) В стереометрии: Вычисление длины диагонали прямоугольного параллелепипеда
- 14. Спасибо за внимание!
Теорема Пифагора:Сумма квадратов катетов равна квадрату гипотенузы.a² + b² = c² ( где а,b – катеты, с – гипотенуза)
Слайд 1Применение теоремы Пифагора
Работу подготовила
Ученица 8 класса А
Школы №47 города Рязани
Пискунова
Слайд 2Теорема Пифагора:
Сумма квадратов катетов равна квадрату гипотенузы.
a² + b² = c²
( где а,b – катеты, с – гипотенуза)
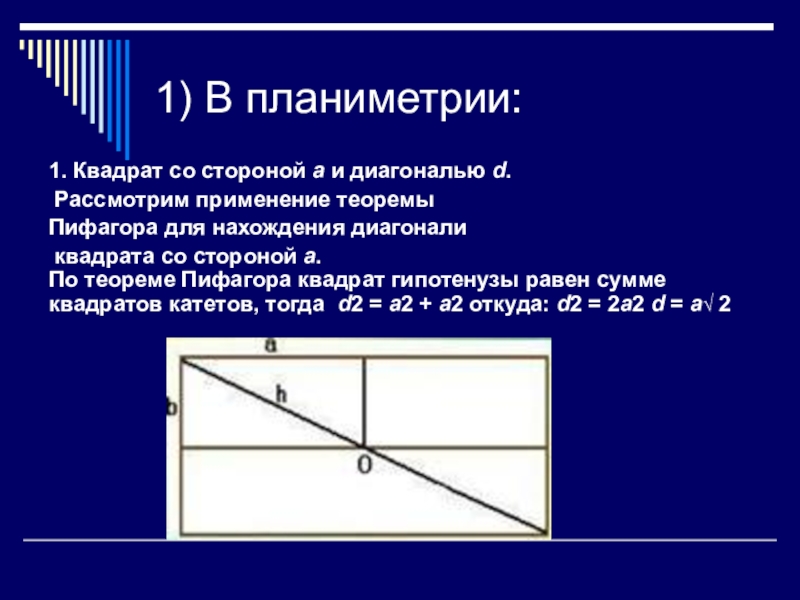
Слайд 41) В планиметрии:
1. Квадрат со стороной а и диагональю d.
Рассмотрим применение теоремы
Пифагора
для нахождения диагонали
квадрата со стороной а. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, тогда d2 = a2 + a2 откуда: d2 = 2a2 d = а√ 2
квадрата со стороной а. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, тогда d2 = a2 + a2 откуда: d2 = 2a2 d = а√ 2
Слайд 52. Диагональ d прямоугольника со сторонами а и b вычисляется подобно
тому, как вычисляется гипотенуза прямоугольного треугольника с катетами a и b.
По теореме Пифагора: d2 = a2 + b2
По теореме Пифагора: d2 = a2 + b2
Слайд 63.Высота h равностороннего треугольника со стороной а может рассматриваться как катет прямоугольного треугольника, гипотенуза которого а,
а другой катет a/2. Таким образом по теореме Пифагора
а2 = h2 + (1/2a)2 h2 = a2 – (1/2a)2 h = 1/2a √ 3
а2 = h2 + (1/2a)2 h2 = a2 – (1/2a)2 h = 1/2a √ 3
Слайд 72) В архитектуре:
В зданиях готического и ромaнского стиля верхние части
окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле.
Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг и половине ширины (b/2), для внутренних дуг.
Слайд 8Остается еще полная окружность, касающаяся четырех дуг. Так как она заключена
между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; покажем, как применяется в таких задачах теорема Пифагора.
Слайд 9В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает
ширину окна, то радиусы полуокружностей будут равны R = b/2 и r = b/4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4 + p, один катет равен b/4, а другой b/2 – p.
По теореме Пифагора имеем: (b/4 + p)2 = (b/4)2 + (b/2 – p)2
Решив данное уравнение, легко найти радиус внутренней окружности р = b/6
Слайд 113) В строительстве:
Если рассматривать треугольную призму как крышу башни, то
в первом нашем вопросе речь идёт о том, какой длины нужно сделать боковые рёбра, чтобы при данной площади чердака была выдержана предписанная высота крыши. Заметим, что расчёт площади кровли можно сильно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит:
Чтобы найти площадь поверхности двухскатной крыши, все скаты которой имеют равный уклон, нужно умножить площадь чердака Sч на длину стропила и разделить на половину ширины дома.
Например, при строительстве любого сооружения рассчитывают расстояния, центры тяжести, размещение опор, балок и т.д. В целом значение теоремы кроме вышесказанного в том, что она применяется практически во всех современных технологиях, а также открывает простор для создания и придумывания новых.
Слайд 124) В физике:
Молниеотвод, громоотвод, устройство для защиты зданий, промышленных, транспортных, коммунальных,
с-х. и других сооружений от ударов молнии.
Известно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
По теореме Пифагора h2 > a2 + b2,
_______
значит h > √a2 + b2
По теореме Пифагора h2 > a2 + b2,
_______
значит h > √a2 + b2